牛客 小白115 20250427
牛客 小白115 20250427
https://ac.nowcoder.com/acm/contest/107879
A:
题目大意:
void solve(){
int a,b,c;
cin>>a>>b>>c;
if (a==b||b==c || b==0&&a==c || b!=0&&a!=0&&c!=0){
cout<<"NO";
return;
}
if (a==0&&b!=0&&c!=0 || c==0&&a!=0&&b!=0){
cout<<"NO";
return;
}
cout<<"YES";
return;
}
签到
B:
题目大意:给出 \(n\) 个元素的数组 \(a\),选出 \(m\) 个元素,使得其中元素值最小的元素的数量最大
int cnt[200010];
void solve(){
int n,m;
cin>>n>>m;
vector<int> a(n+1);
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cnt[a[i]]++;
int sum=0;
int ans=0;
for (int i=200000;i>=1;i--){
sum+=cnt[i];
if (sum>=m) ans=max(ans,min(cnt[i],m));
}
cout<<ans;
}
排序后从后往前计算,如果当前可以选出的总数大于了 \(m\) ,则可以计算当前元素对答案的贡献
考虑用桶记录元素的数量,从后往前计算时,当前枚举的元素值一定是最小的
C:
题目大意:

int a[200010];
int pre[200010];
int suf[200010];
int cnt[110];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
int q,v;
cin>>q>>v;
for (int i=1;i<=n;i++){
if (a[i]>v)
pre[i]=pre[i-1]+1;
else
pre[i]=pre[i-1];
}
for (int i=n;i>=1;i--){
for (int j=a[i]+1;j<=100;j++) suf[i]+=cnt[j];
cnt[a[i]]++;
}
int ans=1e9;
for (int i=1;i<=n;i++)
ans=min(ans,pre[i-1]+suf[i]);
cout<<ans;
}
数据范围较小,可以用 \(O(nv)\) 的时间复杂度计算
因为只有一次扭转乾坤的机会,所以对于每个射来的子弹,如果对这颗子弹使用扭转乾坤,那么转瞬即逝的使用次数取决于这个子弹之前危险值大于初始运气值的数量,加上这个子弹之后危险值大于这颗子弹的危险值的数量
所以对于每颗子弹都预处理出他的前缀和后缀,又因为 \(a_i\le 100\) ,所以计算后缀时可以用桶暴力的 \(O(nv)\) 计算
最后答案就为前缀加上后缀的最小值
D:
题目大意:

string s[100005];
vector<vector<int>> cnt(200010,vector<int>(30,0));
void solve() {
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>s[i];
int g=0;
for (int i=1;i<=n;i++)
g=__gcd(g,(int)s[i].size());
for (int i=1;i<=n;i++)
for (int k=0;k<s[i].size();k++)
cnt[k%g][s[i][k]-'a']++;
int ans=0;
for (int k=0;k<g;k++) {
int sum=accumulate(cnt[k].begin(),cnt[k].end(),0);
int mx=*max_element(cnt[k].begin(),cnt[k].end());
ans+=sum-mx;
}
cout<<ans;
}
如果 \(a,b\) 字符串存在最小公倍字符串,那么这两个字符串一定存在完全相同的循环节
循环节的长度为这两个字符串长度的最大公约数,那么如果任意的两个字符串间都有最小公倍字符串,所以所有的字符串都由相同的循环节构成
int g=0;
for (int i=1;i<=n;i++)
g=__gcd(g,(int)s[i].size());
计算完循环节的长度后,现在需要考虑如何让操作次数最小化
设循环节为 \(p\) ,那么满足题意的所有字符串都可以被表示为 \(k*p,k\in N^+\) ,将所有的字符串拆解为循环节后,记录在循环节这一位上的每个字符所有的数量
for (int i=1;i<=n;i++)
for (int k=0;k<s[i].size();k++)
cnt[k%g][s[i][k]-'a']++;
当前字符串的这个字符 \(s_k\) 处于循环节的第 \(k\% g\) 个位次上,用cnt[i][j] 记录循环节的第 \(i\) 位是字符 \(j\) 的数量
for (int k=0;k<g;k++) {
int sum=accumulate(cnt[k].begin(),cnt[k].end(),0);//计算当前位上的字符总数
int mx=*max_element(cnt[k].begin(),cnt[k].end());//计算当前位上最多的字符
ans+=sum-mx;
}
遍历循环节每一位上字符的数量,如果钦定这一位上的字符为 \(c\) ,那么需要的操作数为所有字符总数减去这个字符的数量
要使得操作数最小,那么钦定的这个字符的数量就是当前位上数量最多的字符,累加答案即可
E
题目大意:

int a[200010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
map<int,int> mp;
for (int i=n;i>=1;i--){
if (!mp[a[i]+1])
mp[a[i]+1]++;
else if (!mp[a[i]-1])
mp[a[i]-1]++;
else{
cout<<"NO"<<endl;
return ;
}
}
int cnt=0,pos=0;
for (auto [k,v]:mp){
cnt+=k-pos-1;
pos=k;
cnt-=1;
if (cnt<0){
cout<<"NO"<<endl;
return ;
}
}
cout<<"YES"<<endl;
return ;
}
首先考虑无解的情况:当前时间上存在两个魔法师需要同时应对那么一定无解
两个卷轴对魔法师产生的效果相当于将这个魔法师的吟唱时间前移一次或者后移一次,对同一个魔法师使用两次相同的卷轴一定劣
所以,题意可以转化为怎样去改变安排魔法师的位次使得任意时间上不存在两个魔法师需要应对
显然是尽量使得魔法师的吟唱时间越靠后越优,这样前面就有更多的时间进行操作
那么对一个魔法师 \(a_i\) ,在 \(a_i+1\) 合法的情况下将他后移一定优,并且需要考虑后续影响性,所以需要从后往前枚举,优先安排更难放置的魔法师
安排完魔法师的位次后,按照时间顺序开始处理爆炸的效果
在应对完一个魔法师后,如果当前的空余操作数小于 \(0\) 就说明无解(没有充足的时间应对这个魔法师)
用 \(cnt\) 记录空余操作数,\(pos\) 记录应对上一个魔法师的时间,那么在应对下一个魔法师时,可以补充的空余操作数为 \(k-pos-1\)
与此同时,应对一个魔法师也需要消耗一次操作,那么每次 \(cnt\) 也要减一
F
题目大意:

int n,m;
int dg[200010];
void solve(){
memset(dg,0,sizeof dg);
cin>>n>>m;
for (int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
dg[u]++;
dg[v]++;
}
int cnt1=0,cnt2=0;
for (int i=1;i<=n;i++){
if (dg[i]%2) cnt1++;
else cnt2++;
}
cnt1/=2;
if (cnt1%2 && cnt2%2==0) cout<<1<<endl;
else cout<<0<<endl;
}
有点诈骗
根据题意,可以得到三种样式的连通块:一条链,一个节点,一个环,分别考虑这三种对答案的影响
- 一条链:当链上的节点数为偶数时,先手得分为 \(1\),链上节点数为奇数时,都不得分
- 一个环:无论环上有多少个节点,都不得分
- 一个节点:显然都不得分
所以当存在链时,才会有得分,下面基于链上考虑选点的优劣性,用 \(A,B\) 表示先后手
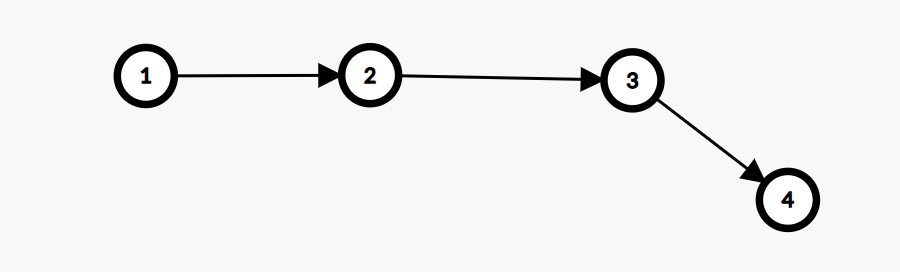
A:1 B:2
A:3 B:4
//先手得分
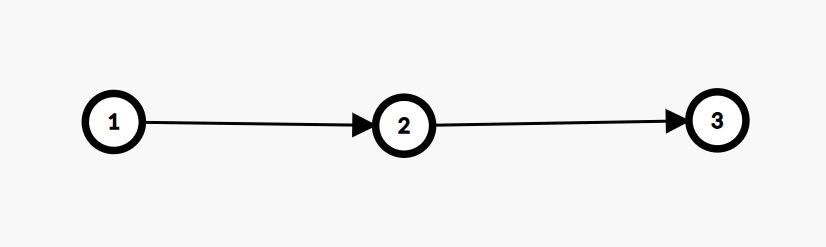
A:1 B:2
A:3
//都不得分
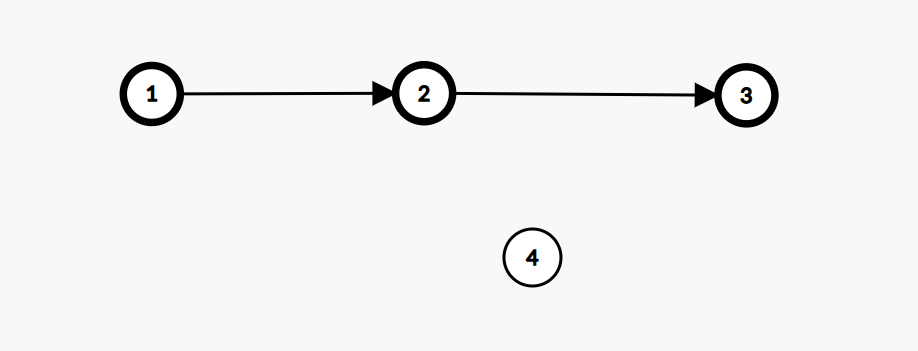
A:1 B:2
A:4 B:3
观察上面的三种状况可以知道,对于任意一个处在环上或单独的一个节点都可以被等效为在一条链上度数为 \(2\) 的节点
所以给定的整张图都可以被抽象为许多条链构成的图
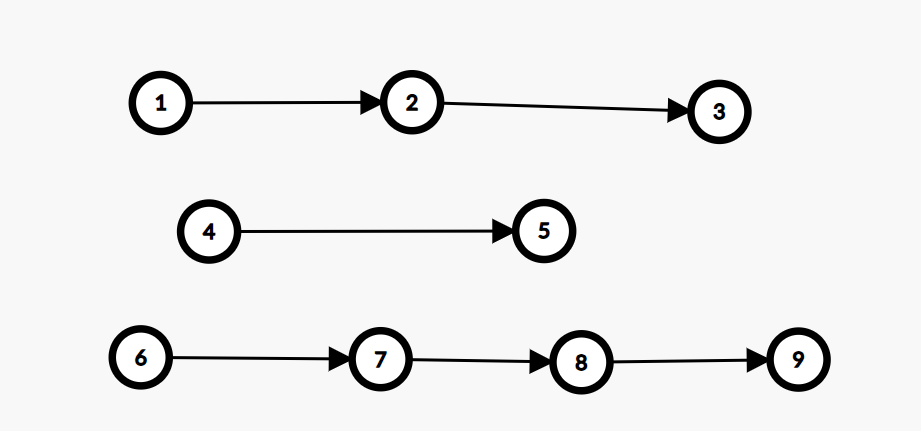
更进一步,根据度数的不同这张图可以再把链抽象为仅有两个节点的链(两个度数为 \(1\) 的节点)和一些单独的节点

两人轮流选择链首节点一定是最优的,选完链后,就选单独的节点,根据单独节点数量的奇偶性判断链尾元素的先后顺序
得到最终结论:先手得分时,当且仅当链个数为奇数且单独节点个数为偶数,否则都不得分
G
题目大意:

// Problem: 命运之弹(Hard Version)
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/107879/G
// Memory Limit: 512 MB
// Time Limit: 4000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long
#define Lc p<<1
#define Rc p<<1|1
#define lc(x) tr[x].ch[0]
#define rc(x) tr[x].ch[1]
using namespace std;
const int N=2e5+10;
struct node{
int l,r,mn,add;
};
node tr[4*N];
int a[N];
pair<int,int> qry[N];
int num[N];
vector<pair<int,int>> pp;
int ans[N];
void build(int l,int r,int p){
tr[p]={l,r,pp[l].second,0};
if (l==r) return;
int mid=l+r>>1;
build(l,mid,Lc);
build(mid+1,r,Rc);
tr[p].mn=min(tr[Lc].mn,tr[Rc].mn);
}
void pushdown(int p){
if (tr[p].add){
tr[Lc].mn+=tr[p].add;
tr[Rc].mn+=tr[p].add;
tr[Lc].add+=tr[p].add;
tr[Rc].add+=tr[p].add;
tr[p].add=0;
}
}
void update(int x,int y,int k,int p){
if (x<=tr[p].l&&y>=tr[p].r){
tr[p].mn+=k;
tr[p].add+=k;
return ;
}
int mid=tr[p].l+tr[p].r>>1;
pushdown(p);
if (x<=mid) update(x,y,k,Lc);
if (y>mid) update(x,y,k,Rc);
tr[p].mn=min(tr[Lc].mn,tr[Rc].mn);
}
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
pp.push_back({-1,-1});
int mx=0,idx=0;
for (int i=1;i<=n;i++){
if (a[i]>mx){
mx=a[i];
pp.push_back({i,0});
num[i]=++idx;
}
}
vector<int> st(a+1,a+n+1);
sort(st.begin(),st.end());
for (auto &[x,y]:pp)
if (x!=-1)
y=st.size()-(upper_bound(st.begin(),st.end(),a[x])-st.begin());
build(1,pp.size()-1,1);
int q;
cin>>q;
for (int i=1;i<=q;i++){
cin>>qry[i].first;
qry[i].second=i;
}
sort(qry+1,qry+q+1);
vector<pair<int,int>> stp;
stp.push_back({-1,-1});
for (int i=1;i<=n;i++) stp.push_back({a[i],i});
sort(stp.begin()+1,stp.end());
set<int> sav;
for (auto [x,y]:pp)
if (x!=-1)
sav.insert(x);
int ord=stp.size()-1;
for (int i=q;i>=1;i--){
auto [x,y]=qry[i];
while(ord>=1&&stp[ord].first>x){
int d=stp[ord].second;
auto f=sav.upper_bound(d);
if (f!=sav.end())
update(num[*f],idx,1,1);
ord--;
}
ans[y]=tr[1].mn;
}
for (int i=1;i<=q;i++) cout<<ans[i]<<endl;
}
int main()
{
cintie;
solve();
return 0;
}
线段树+离线化,在 easyversion 的基础上优化
事实上,进行扭转乾坤的操作只会对一部分子弹进行,换句话说,某些子弹进行扭转乾坤后一定劣
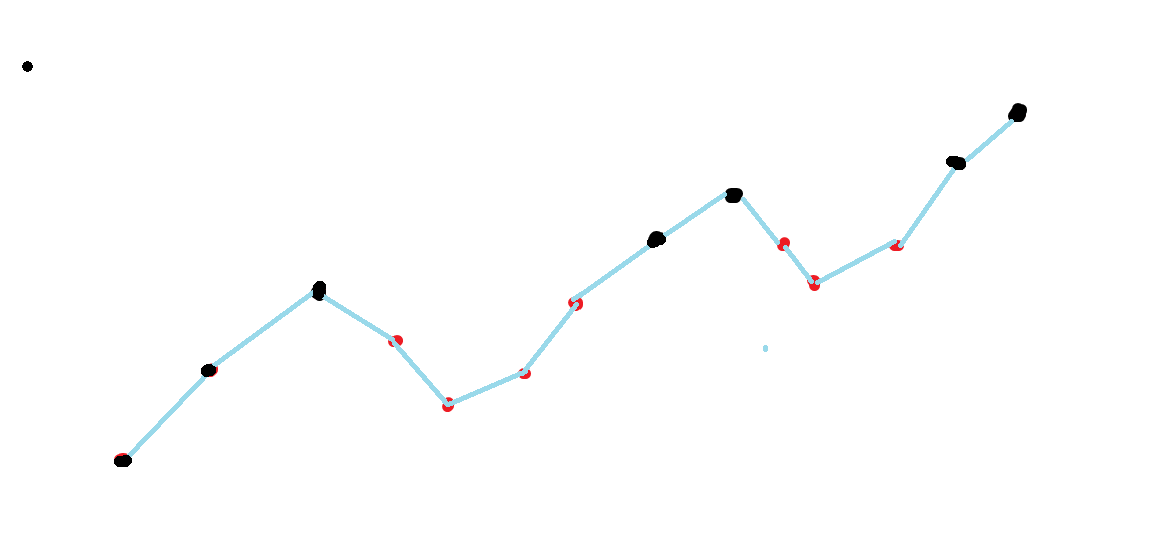
将子弹的危险值转化为折线图,对图上红色点进行扭转乾坤的操作一定劣,因为如果为红色,那么他的前面一定存在比他危险值更大的子弹,对这个危险值大的子弹进行操作一定优于他,所以我们需要对黑色点对应的子弹(可考虑子弹)进行处理
vector<pair<int,int>> pp;
pp.push_back({-1,-1});
int mx=0,idx=0;
for (int i=1;i<=n;i++){
if (a[i]>mx){
mx=a[i];
pp.push_back({i,0});//记录可考虑点的是第几颗子弹
num[i]=++idx;
}
}
对于每个可考虑子弹,类似的需要计算在他之后危险值大于他的子弹个数
vector<int> st(a+1,a+n+1);//计算数组
sort(st.begin(),st.end());//从小到大排序后
for (auto &[x,y]:pp)
if (x!=-1)
y=st.size()-(upper_bound(st.begin(),st.end(),a[x])-st.begin());//计算在这个可考虑子弹后危险值大于他的子弹个数
这样计算的原理是,新开一个 st 数组,复制原来子弹序列,然后从小到大排序
对于可考虑子弹 \(a_i\),在他之后危险值大于他的子弹个数可由所有子弹数减去他之前小于他的子弹个数的值计算(upper_bound 计算)
定义每个可考虑子弹在 \(v\) 下答案为两部分:\(pre,suf\) 即在这个可考虑子弹前,大于运气值的子弹个数以及在这个可考虑子弹后,大于这个可考虑子弹的危险值的子弹的个数
这两步下来,我们就已经处理好了所有可选择子弹在子弹序列中的编号,已经他之后危险值大于他的子弹个数 \(suf\)
现在还需要计算在可考虑子弹前,大于运气值的子弹个数,由于数据量大,所以需要对询问进行离散化处理
int q;
cin>>q;
for (int i=1;i<=q;i++){
cin>>qry[i].first;
qry[i].second=i;
}
sort(qry+1,qry+q+1);//从小到大排序
离散化处理的原因是,对于每个询问的 \(v\) ,如果可以利用上一次询问的部分信息,那么可以降低时间复杂度
从大到小处理询问的 \(v\) ,对于每一个危险值大于 \(v\) 的子弹 \(a_d\) ,他对答案的贡献是对在 \(d\) 之后的可考虑子弹的 \(pre+1\)
利用线段树处理区间更改操作,以及维护全局最小值(最小转瞬即逝次数)
vector<pair<int,int>> stp;
stp.push_back({-1,-1});
for (int i=1;i<=n;i++) stp.push_back({a[i],i});//stp记录每个子弹的危险值和编号
sort(stp.begin()+1,stp.end());
set<int> sav;
for (auto [x,y]:pp)
if (x!=-1)
sav.insert(x);//记录可考虑点的编号
int ord=stp.size()-1;
for (int i=q;i>=1;i--){//从大到小处理询问
auto [x,y]=qry[i];
while(ord>=1&&stp[ord].first>x){//找所有危险值大于当前v的子弹
int d=stp[ord].second;//找到这个子弹的位置
auto f=sav.upper_bound(d);//计算出编号大于这个子弹的可考虑子弹
if (f!=sav.end())//如果能找到
update(num[*f],idx,1,1);//计算这个子弹对答案的贡献
ord--;
}
ans[y]=tr[1].mn;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号