9.21

 

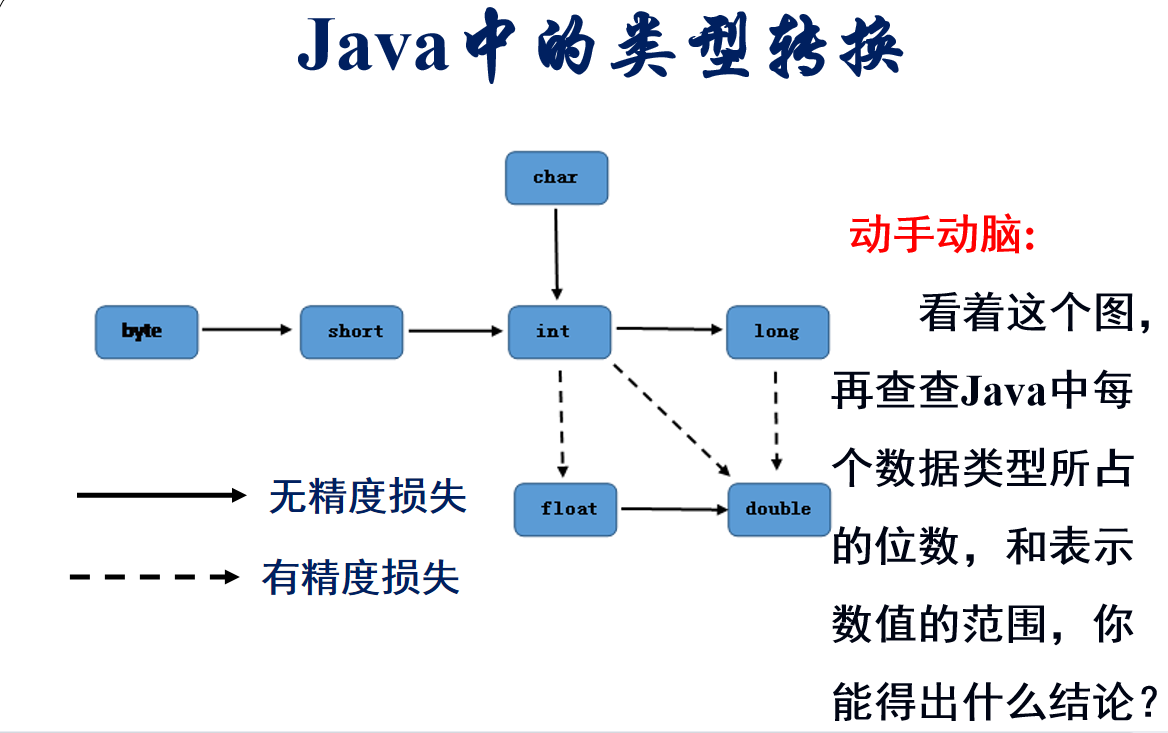
得出的结论是表示数据范围小的向大的转化是无精度损失，小的向大的可能会出现精度损失。

 

 

 

 输出的结果，前半部分的数值是精确的后半部分的数值开始出现偏差并且每次运行的结果偏差都不同，浮点数并不精确。

为什么double类型的数值进行运算得不到“数学上精确”的结果？

double类型的数值占用64bit，即64个二进制数，除去最高位表示正负符号的位，在最低位上一定会与实际数据存在误差(除非实际数据恰好是2的n次方)。

比如要用4bit来表示小数3.26，从高到低位依次对应2的1,0,-1,-2次幂，根据最上面的分析，应当在二进制数11.01(对应十进制的3.25)和11.10(对应十进制的3.5)之间选择。

简单来说就是我们给出的数值，在大多数情况下需要比64bit更多的位数才能准确表示出来(甚至是需要无穷多位)，而double类型的数值只有64bit，后面舍去的位数一定会带来误差，无法得到“数学上精确”的结果。
————————————————
版权声明：此段为CSDN博主「設計師·Rainbow」的原创文章。
原文链接：https://blog.csdn.net/weixin_33417371/article/details/114705885

 

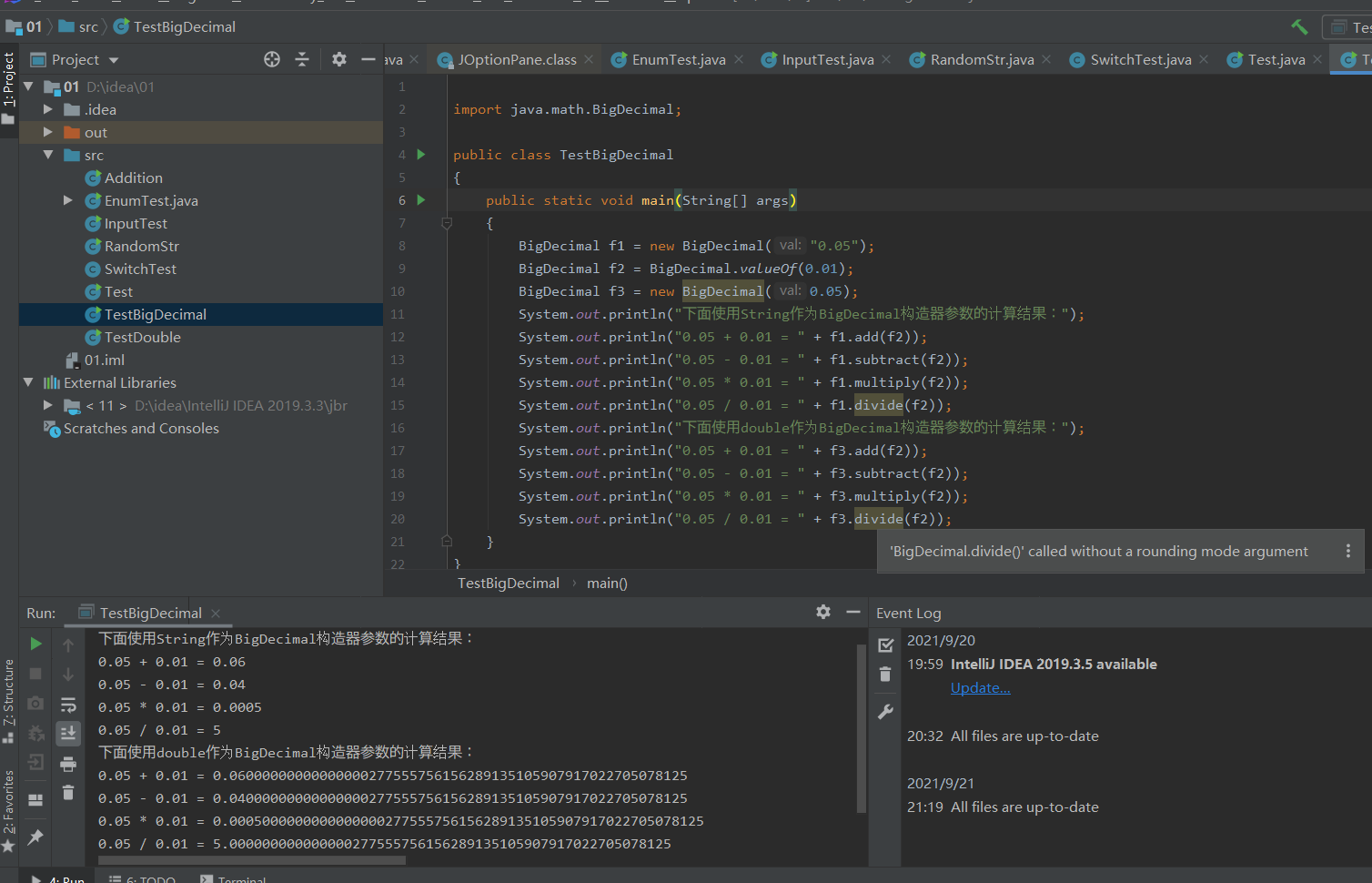
 构建BigDecimal对象时应使用字符串而不是double数值，否则，仍有可能引发计算精度问题。

double并不能准确的代表BigDecimal 16位有效数以上的数字在使用BigDecimal时创建对象。而BigDecimal所创建的对象不能使用+-*/等传统的算术运算符直接对其对象进行数学运算，必须调用相对应的(f1.add(f2))等方法。 因为方法中的参数必须是BigDecimal的对象，所以定义时应为字符串。
————————————————
版权声明：此段为CSDN博主「設計師·Rainbow」的原创文章。
原文链接：https://blog.csdn.net/weixin_33417371/article/details/114705885