散列·开放定址法
一、介绍
分离链接散列算法的缺点是使用链表。在新单元分配地址需要时间,不同的语言需要的时间不一致,这会导致算法的速度有些减慢。分离链接法也是固定定址的一种,与之对应的另有一种叫开放定址法,意味着散列算法得到的地址不是固定的,或者说不是一定要遵守的。
开放定址
在散列算法得到一个存储地址之后,如果发生冲突,不是在原处创建一个链表而是按照一定规则寻找周围可用的地址进行插入。
二、线性探测法
2.1 定义
在线性探测法中,函数\(f\)是\(i\)的函数,记为:\(f(i) = i\) 。(\(i\):寻址次数)这相当于相继探测每个单元。例子:我们在M=10点散列表中,按顺序插入下列数字{89,18,49,58,69}
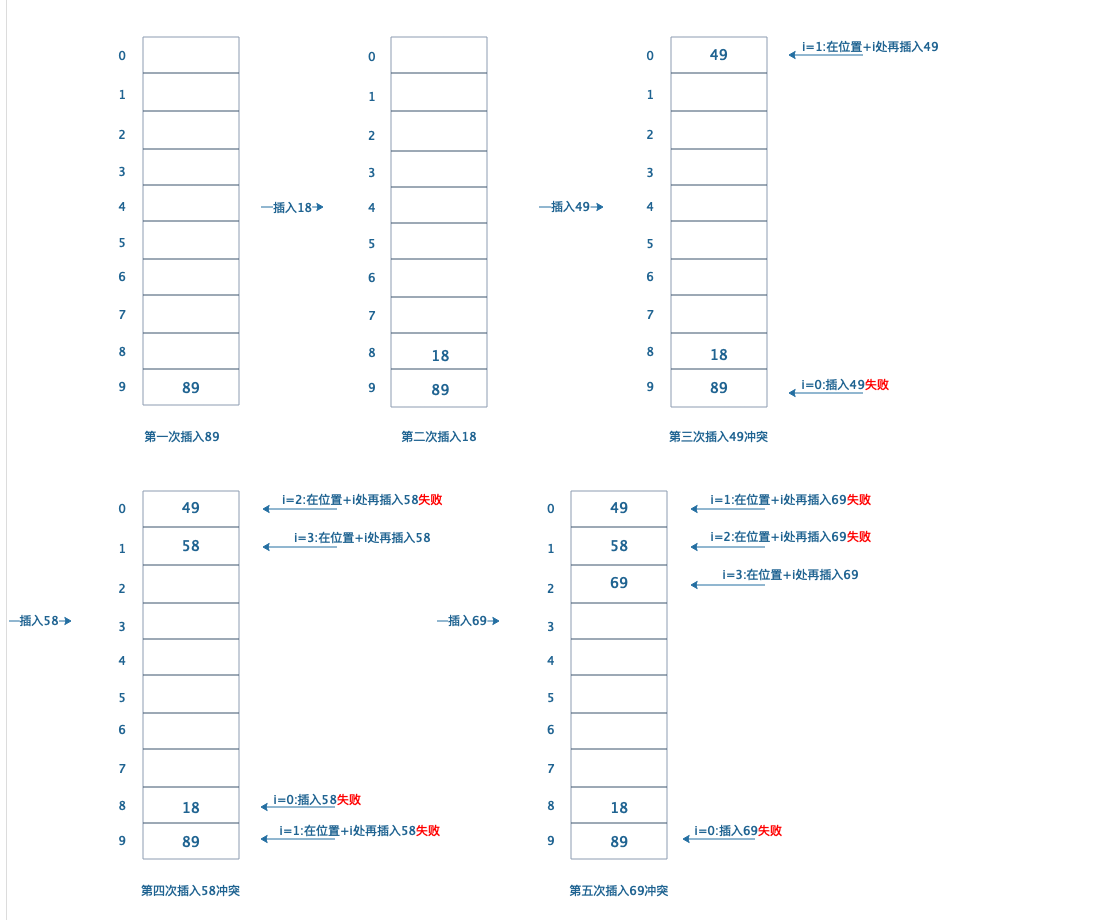
2.2 过程说明:
按照散列方式,在插入89和18时,直接插入到散列位置9和位置8。但是插入第三个数49时,散列位置为9,跟已有89冲突,于是开始线性探测,即按照顺序寻找下一个位置。\(i=1\)时,探测位置为散列位置M+\(i\),即探测位置0,位置0无冲突,49存入位置0。插入第四个树58时,散列位置M=8,但是位置8已经存在18,发生冲突开始线性探测,\(i=1\)时,探测位置为散列位置M+$$i$$,位置9已有89存在发生冲突,\(i=2\)时,探测位置为0,位置0已有49存在,发生冲突,\(i=3\)时,探测位置1,位置1无冲突,58存入位置1。同理,69在探测到第3次后,存入位置2。
2.3 结果说明
2.3.1 一次聚集
很明显根据图形发现,当我们在位置9冲突时,寻址方式都是从0开始往后推,意味着,存入的数组不再是我们想要的均匀的。而是会根据探测路径聚合在一起,比如上图的0,1,2。这种情况叫做一次聚集。明显是我们不想要的。
2.3.2 效率
\(\lambda\)为装填因子
1. 插入和不成功的查找:\(\frac 12(1+1/(1-\lambda)^2)\)。
2. 成功的查找:\(\frac 12(1+1/(1-\lambda))\)。
证明过程有点坑啊,不过小问题,我们用分析来说明下。公式一,不成功的查找,意味着每次都要产生冲突,每次都要冲突,如果数量为N,N=1时,需要比较1次,N=2时,需要比较2次,依次推理,在M大小的散列表中含有N个数,总结和分析,近似值为公示一。公式二,成功的查找,意味着每次都能正确找到,或者允许一定限度内的冲突,得到公式二。
性能:
对于线性探测法,\(\lambda\)的选择时非常重要的,\(\lambda\)越大,越容易发生聚集。如果当表的大小不是素数时,而且\(\lambda\)接近或大于1/2时,我们甚至无法一次就找到空单元,每次插入都需要探测之后。
三、平方探测法
3.1 定义
在线性探测法中,函数\(f\)是\(i\)的函数,记为:\(f(i) = i\) 。而在平方探测法中,我们通常使用的是\(f(i) = i^2\) 。还是上面的例子,我们利用平方探测法插入{89,18,49,58,69}
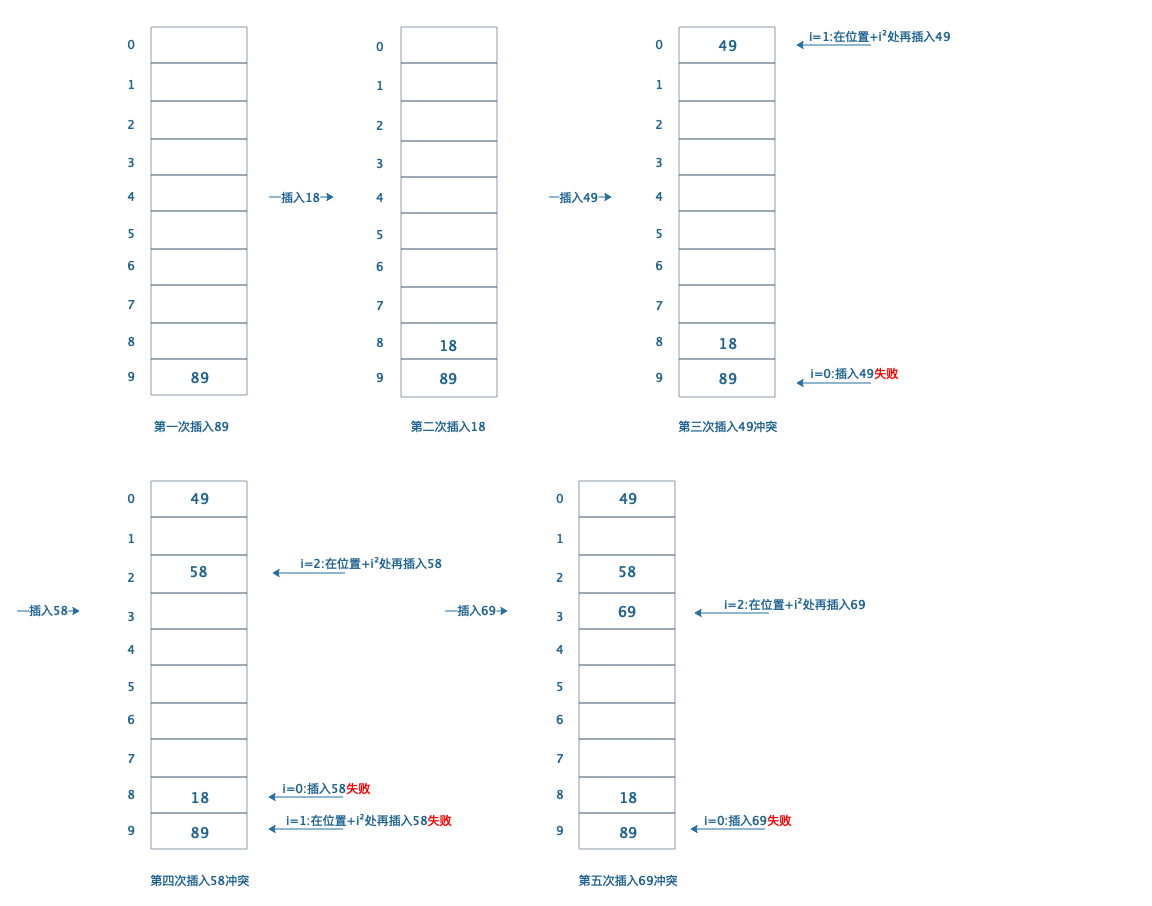
3.2 过程说明:
按照散列方式,在插入89和18时,直接插入到散列位置9和位置8。但是插入第三个数49时,散列位置为9,跟已有89冲突,于是开始平方探测,第一次探测\(i = 1, f(i)=i^2 = 1\),所以我们探测位置为位置0(位置9+1)。发现位置0不冲突,那么在位置0插入49。插入第四个数58时,散列位置8,跟已有18冲突,开始平方探测,第一次探测\(i = 1, f(i)=i^2 = 1\),探测位置9(位置8+1),发生冲突!第二次探测\(i = 2, f(i)=i^2 = 4\),探测位置2(位置8+4),位置2不冲突,在位置2插入58。第五次插入同理。
3.3 结果说明
明显,当发生冲突时,我们探测的位置跨度较大,不再是一个个探测,这样有效的避免的一次聚集。
3.3.1 二次聚集
按照现有的逻辑,一次聚集可以避免,但是有个问题:如果散列到同一个位置的数,将会探测相同的位置。比如上面那个粗糙的例子,插入18,28,38,48时,他们明显会探测相同的位置。我们称这种叫做二次聚集。
3.3.2 效率
或者称之为有效性:如果表有一半是空的,并且表的大小是素数,那么我我们保证总能插入一个新的元素。
在这么这个有效性之前,我们先解读一下。\(\lambda\) <= 1/2,有一半的位置可以用作备选位置。
证明:我们有很多方法都可以证明,这是个简单的问题,这里按照书上的证明过程,因为很容易理解。
令__表的大小\(M\)__是一个大于3的素数。我们证明:前[M/2]个备选位置,是互异的。\(h(x)+i^2\)和\(h(x)+j^2\)是这些位置中的两个,其中\(0\leq i,j \leq [M/2]\)。假设法:假设这两个位置相同,但\(i \ne j\),
由于\(i\)和\(j\)是互异的,\(i \neq j\),但是\(0\leq i,j \leq [M/2]\),所以上述公式无法成立。则假设不成立,得到结论:如果最多有M/2个位置被使用,那么空单元总能够找到。
即使表被填充的位置仅仅比一半多一个,那么上述定理都不再成立,插入可能失败。
3.3.3 素数
表大小使用素数很重要,因为素数的重要特性:只能被0和它自身整除,这意味着在0和它之间的所有数进行散列时,整个表都可以被探测到。
3.4 删除
关于探测表的操作,在探测散列表中不能进行标准的删除操作,因为相应的单元可能引起过冲突,元素绕过它存到了别处。比如上述例子,我要删除49,那么散列定位的位置是9,但是位置9并不是需要删除的49。49因为冲突而被插入到了其他地方。所以删除的操作需要进行一定的修饰,我们可以使用懒惰删除。
四、双散列
4.1 定义
双散列中,我们通常用的算法是:\(f(i) = i·{hash_2}(x)\)。不得不说,这个散列方法,对于\({hash_2}(x)\)的选择至关重要,这个公式的要求是,当发生冲突时,我们的探测位置,将根据第二个散列算法来决定。我们第一次散列算法\(hash(x)\)得到我们的初始位置 ,但是初始位置发生冲突,我们需要探测下一个位置为“探测次数 * 另一个散列算法\({hash_2}(x)\)。
图表以及说明都可以参考上文的二和三。以此类推。
4.2 结果说明
散列结果显而易见,其实跟平方探测时一个类型的。
所以在实践中,若非必要,平方探测法的使用取代双散列,毕竟${hash_2}(x)$也是需要时间的。效率明显不如平方探测。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号