卡特兰数及应用

卡特兰数

卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。
以比利时的数学家欧仁·查理·卡特兰（1814–1894）命名。
历史上，清代数学家明安图(1692年－1763年)在其《割圜密率捷法》中最先发明这种计数方式，远远早于卡塔兰。
有中国学者建议将此数命名为“明安图数”或“明安图-卡塔兰数”。

卡塔兰数的一般项公式为

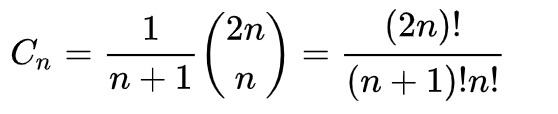
递推关系

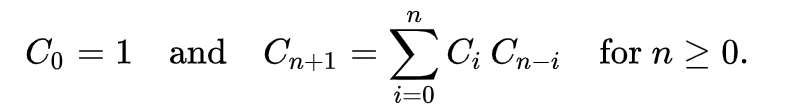
由递推关系很容易得出他的另一个表达式：

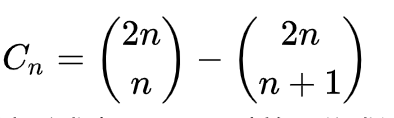
前20项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190
（来自维基百科）

排列组合

先来看一下数学基础
组合的定义：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。

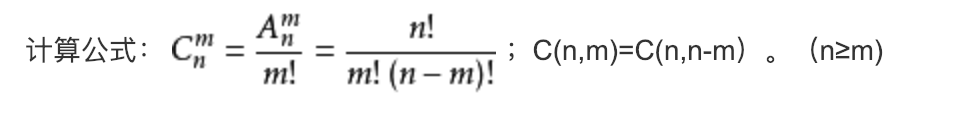
应用

很多不起眼的地方都会涉及到卡特兰数的公式。

Dyck word

Dyck word是一个有n个X和n个Y组成的字串，且所有的前缀字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

括号序列

将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数：
((())) ()(()) ()()() (())() (()())

思路2: n对括号相当于有2n个符号，n个左括号、n个右括号，可以设问题的解为f(2n)。第0个符号肯定为左括号，与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符，那么第0个字符与第2i个字符间包含奇数个字符，而奇数个字符是无法构成匹配的。
通过简单分析，f(2n)可以转化如下的递推式 f(2n) = f(0)f(2n-2) + f(2)f(2n - 4) + ... + f(2n - 4)f(2) + f(2n-2)f(0)。简单解释一下，f(0) * f(2n-2)表示第0个字符与第1个字符匹配，同时剩余字符分成两个部分，一部分为0个字符，另一部分为2n-2个字符，然后对这两部分求解。f(2)*f(2n-4)表示第0个字符与第3个字符匹配，同时剩余字符分成两个部分，一部分为2个字符，另一部分为2n-4个字符。依次类推。
假设f(0) = 1，计算一下开始几项，f(2) = 1, f(4) = 2, f(6) = 5。结合递归式，不难发现f(2n) 等于h(n)。

出栈问题

一个栈（无穷大）的进栈次序为1、2、3……n。不同的出栈次序有几种。

思路1:，我们设f(n)=序列个数为n的出栈序列种数。同时，我们假定，从开始到栈第一次出到空为止，这段过程中第一个出栈的序数是k。特别地，如果栈直到整个过程结束时才空，则k=n。首次出空之前第一个出栈的序数k将1_{n的序列分成两个序列，其中一个是1}k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。此时，我们若把k视为确定一个序数，那么根据乘法原理，f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n+1)(n=0，1，2，……)。最后，令f(0)=1，f(1)=1。

出栈入栈问题有许多的变种，比如n个人拿5元、n个人拿10元买物品，物品5元，老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是，由于每个拿5元的人排队的次序不是固定的，所以最后求得的答案要n!。拿10元的人同理，所以还要n!。所以这种变种的最后答案为h(n)n!n!。

思路3: 队伍的序号标为0,1,...,2n-1,并把50元看作左括号，100元看作右括号，合法序列即括号能完成配对的序列。对于一个合法的序列，第0个一定是左括号，它必然与某个右括号配对，记其位置为k。那么从1到k-1、k+1到2n-1也分别是两个合法序列。那么，k必然是奇数（1到k-1一共有偶数个），设k=2i+1。那么剩余括号的合法序列数为f(2i)*f(2n-2i-2)个。取i=0到n-1累加，并且令f(0)=1，再由组合数C(0,0)=0,可得卡特兰数的递推式。

二叉搜索树排列

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？
n=3时有5种

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

假设结果为f(n)，根可以为1，2，....n,当1为根的时候，左子树为0，右子树的结点为n-1，当2为根节点时，其左子树节点个数为1，右子树节点为n-2。
所以f（n）= f(0)f(n-1)+f(1)(n-2)+...+f(n-1)f(0)。满足卡特兰数的递推式。所以直接用卡特兰数的通项公式：(2n)!/((n+1)!n!);

  var numTrees = function(n) {
        return factorial(2*n)/(factorial(n+1)*factorial(n));
        function factorial(num) {
            if(num < 2) {
                return num;
            } else {
                return num * factorial(num-1);
            }
        }
    };

总结

以上应用思路都可以通用，需要根据题目思考出通用式，如果通用式符合卡特兰数，就可以直接用卡特兰数通项公式计算。

参考：
https://www.cnblogs.com/wuyuegb2312/p/3016878.html
https://blog.csdn.net/doc_sgl/article/details/8880468