面向对象第一单元总结

一、程序分析

1、第一次作业分析

问题分析：

第一次作业要求对含x的多项式求导，形式较简单，可以根据指导书中的形式化表达构建出大正则表达式，从而据此判断格式错误，并提取出有用信息（每一项的指数和x的系数）

要点

• 结构化正则表达式的构建

• 将每个项用hashmap存储，以x的指数为key，整个项为value

• 输出时省区不必要的因子（指数为1）和项（系数为0）

第一次作业的类图：

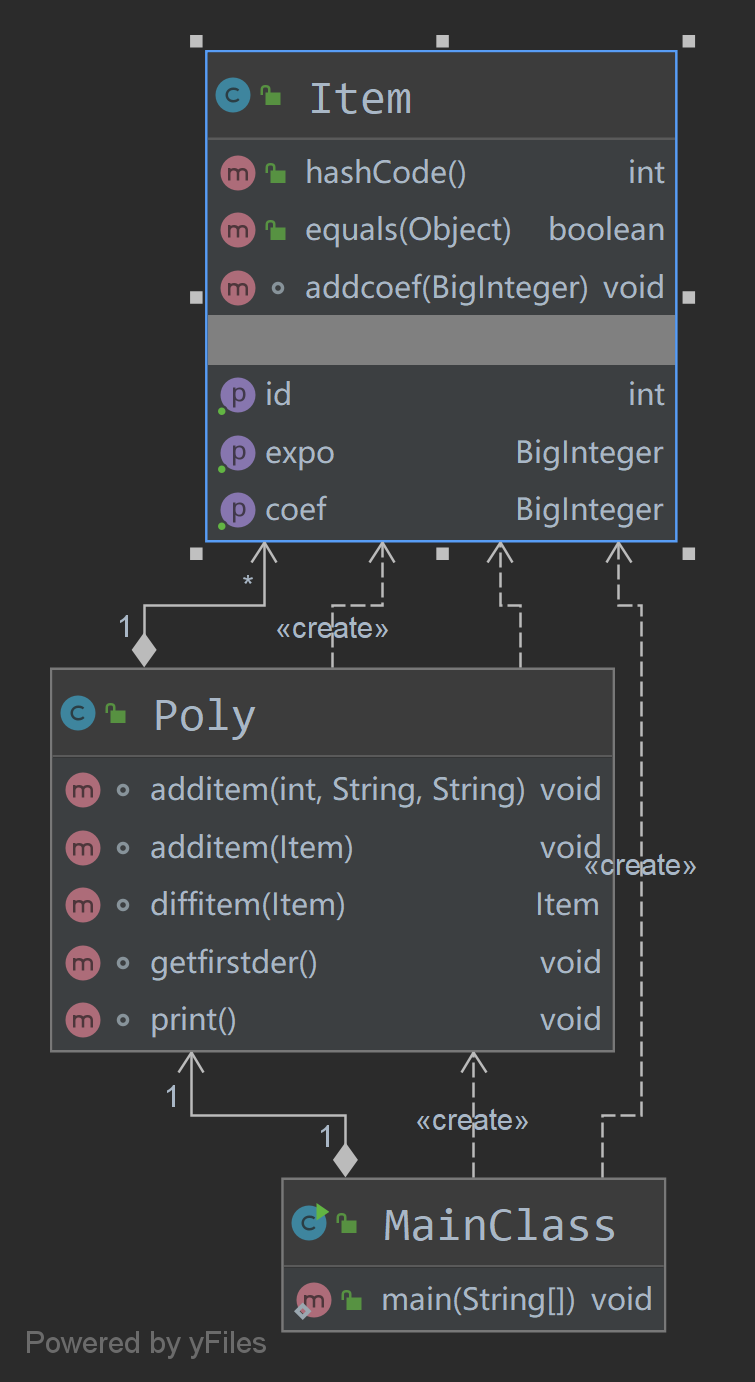
复杂度分析：

Method	ev(G)	iv(G)	v(G)
Item.Item(int,BigInteger,BigInteger)	1	1	1
Item.Item(int,String,String)	1	1	1
Item.addcoef(BigInteger)	1	1	1
Item.equals(Object)	1	2	2
Item.getCoef()	1	1	1
Item.getExpo()	1	1	1
Item.getId()	1	1	1
Item.hashCode()	1	1	1
MainClass.main(String[])	1	20	21
Poly.additem(Item)	1	2	2
Poly.additem(int,String,String)	1	2	2
Poly.diffitem(Item)	2	3	3
Poly.getfirstder()	1	3	3
Poly.print()	2	11	12

bug分析：第一次作业在互测和强测中未发现bug

总结：

第一次作业时由于情形简单，不管是输入处理还是对项的存储都只能满足简单的场景，未考虑到扩展性，这为第二次作业的重构埋下了伏笔。同时由于此时对于面向对象的特性不够熟悉

2、第二次作业分析

问题分析：

本次作业不再是简单只含有x，无论是输入处理还是求导都变得更加复杂，在这样的情形下必须使用表达式树进行处理；在输入的处理上本次放弃了使用大正则表达式，而是使用了分割+小正则表达式的形式，将整个表达式通过+-分割成不同的项，每一项使用正则表达式判断是否符合格式，然后提取必要信息。由于第一次作业并未考虑到这样的后续的可扩展性，导致了第二次作业整个重构，最后时间不够中测未通过。

要点

• 以+-号为界，将表达式分割后验证格式，若正确再在每一项中提取不同的因子，从而构建表达式树

• 用表达式树递归求导，并递归生成Expre表达式类

• 经过转换，Expre类可以轻松合并并且输出

• 递归求导和递归转换过程中对子树的处理涉及到clone

第二次作业的类图

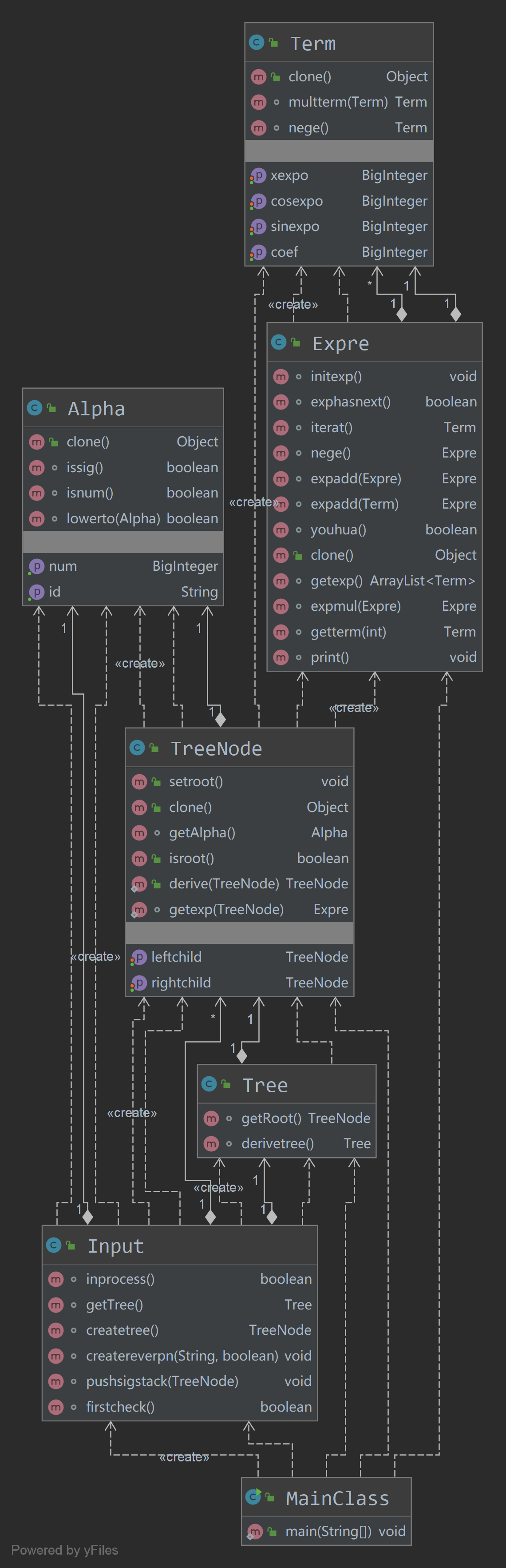
复杂度分析：

Method	ev(G)	iv(G)	v(G)
Alpha.Alpha(BigInteger)	1	1	1
Alpha.Alpha(String,boolean)	1	2	2
Alpha.clone()	3	1	3
Alpha.getId()	1	1	1
Alpha.getNum()	1	1	1
Alpha.isnum()	1	1	1
Alpha.issig()	1	1	1
Alpha.lowerto(Alpha)	3	3	4
Expre.Expre(ArrayList<Term>)	1	1	1
Expre.Expre(Term)	1	1	1
Expre.clone()	1	2	2
Expre.expadd(Expre)	4	6	6
Expre.expadd(Term)	3	5	5
Expre.exphasnext()	1	1	1
Expre.expmul(Expre)	6	7	9
Expre.getexp()	1	1	1
Expre.getterm(int)	1	1	1
Expre.initexp()	1	1	1
Expre.iterat()	1	1	1
Expre.nege()	2	5	5
Expre.print()	2	23	30
Expre.youhua()	6	18	18
Input.Input(String)	1	1	1
Input.createreverpn(String,boolean)	4	17	20
Input.createtree()	3	6	6
Input.firstcheck()	1	1	1
Input.getTree()	1	1	1
Input.inprocess()	11	14	15
Input.pushsigstack(TreeNode)	7	8	10
MainClass.main(String[])	2	1	2
Term.Term(BigInteger,BigInteger,BigInteger,BigInteger)	1	1	1
Term.clone()	1	1	1
Term.getCoef()	1	1	1
Term.getCosexpo()	1	1	1
Term.getSinexpo()	1	1	1
Term.getXexpo()	1	1	1
Term.multterm(Term)	1	1	1
Term.nege()	1	1	1
Term.setCoef(BigInteger)	1	1	1
Term.setCosexpo(BigInteger)	1	1	1
Term.setSinexpo(BigInteger)	1	1	1
Term.setXexpo(BigInteger)	1	1	1
Tree.Tree(TreeNode)	1	1	1
Tree.derivetree()	1	1	1
Tree.getRoot()	1	1	1
TreeNode.TreeNode(Alpha)	1	1	1
TreeNode.clone()	1	3	3
TreeNode.derive(TreeNode)	8	8	10
TreeNode.getAlpha()	1	1	1
TreeNode.getLeftchild()	1	1	1
TreeNode.getRightchild()	1	1	1
TreeNode.getexp(TreeNode)	1	11	13
TreeNode.isroot()	1	1	1
TreeNode.setLeftchild(TreeNode)	1	1	1
TreeNode.setRightchild(TreeNode)	1	1	1
TreeNode.setroot()	1	1	1

bug分析：

第二次作业由于超时，未能通过中测，截至时间前只提交了一份初版，存在大量低级bug，去除低级bug后发现树节点的clone存在bug，在修复clone方法的bug后通过强测。

总结：

完成第二次作业的过程中发现了结构层次对分析问题的重要性，如果结构层次划分得当，那么整个程序架构的可扩展性便能提升几个层次，那这次作业举例，本次作业还是因子间通过*连成项，项之间通过+-连成表达式，这便能将表达式划分成两层，但是若在处理中只按照两层处理便不能处理表达式之间的运算，第三次作业必将重构；若采用树形结构处理，建立表达式树并递归求导，那么整个架构的可扩展性便好很多。

3、第三次作业分析

问题分析：

由于第二次作业已经构建好了表达式树，本次作业只需要处理输入和输出。输入部分，表达式可划分成项，项可划分成因子，但因子又包含了表达式，因此采用正则表达式对整个输入检查时不现实的，但上述结构的划分也提出了问题的解决方法：用三个方法readexp(),readterm(),readfact()通过递归调用分别对上述三个层次进行处理，检测到某一层次便调用相应的read方法，设置好推出条件便完成了输入的处理；输出部分，直接使用树的递归输出很难化简，会包含很多不必要的项，因此可以先将树转换为其他的形式，再化简输出。

要点：

• 层次化通过递归调用处理输入

• 层次化通过递归调用将表达式树转换为易于化简和输出的形式

• 递归调用的时候处理好边界

第三次作业的类图：

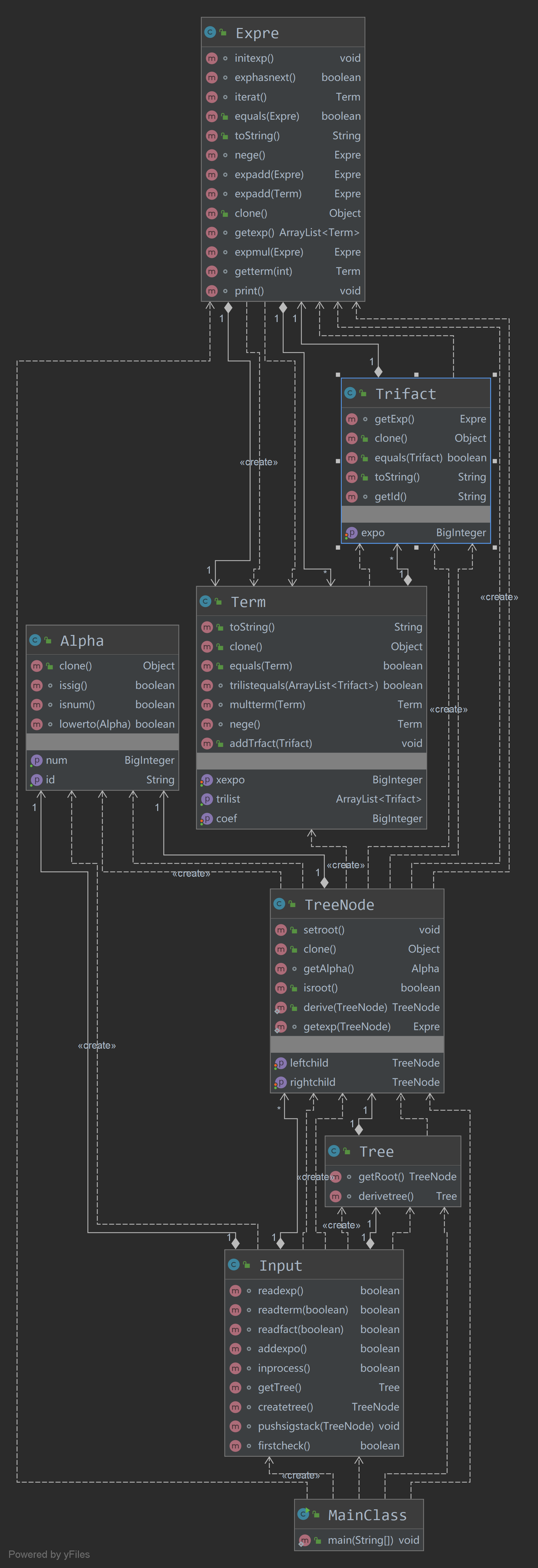
复杂度分析：

Method	ev(G)	iv(G)	v(G)
Alpha.Alpha(BigInteger)	1	1	1
Alpha.Alpha(String,boolean)	1	2	2
Alpha.clone()	3	1	3
Alpha.getId()	1	1	1
Alpha.getNum()	1	1	1
Alpha.isnum()	1	1	1
Alpha.issig()	1	1	1
Alpha.lowerto(Alpha)	4	6	7
Expre.Expre(ArrayList<Term>)	1	1	1
Expre.Expre(Term)	1	1	1
Expre.clone()	1	2	2
Expre.equals(Expre)	6	5	8
Expre.expadd(Expre)	7	11	12
Expre.expadd(Term)	6	9	10
Expre.exphasnext()	1	1	1
Expre.expmul(Expre)	6	7	9
Expre.getexp()	1	1	1
Expre.getterm(int)	1	1	1
Expre.initexp()	1	1	1
Expre.iterat()	1	1	1
Expre.nege()	2	5	5
Expre.print()	2	2	2
Expre.toString()	4	4	7
Input.Input(String)	1	1	1
Input.addexpo()	4	3	4
Input.createtree()	3	6	6
Input.firstcheck()	1	1	1
Input.getTree()	1	1	1
Input.inprocess()	2	2	3
Input.pushsigstack(TreeNode)	8	12	15
Input.readexp()	10	8	15
Input.readfact(boolean)	14	11	18
Input.readterm(boolean)	9	6	12
MainClass.main(String[])	2	2	2
Term.Term(BigInteger,BigInteger)	1	1	1
Term.Term(BigInteger,BigInteger,ArrayList<Trifact>)	1	1	1
Term.Term(BigInteger,BigInteger,Trifact)	1	1	1
Term.addTrfact(Trifact)	5	4	6
Term.clone()	2	3	3
Term.equals(Term)	8	3	14
Term.getCoef()	1	1	1
Term.getTrilist()	1	1	1
Term.getXexpo()	1	1	1
Term.multterm(Term)	1	3	3
Term.nege()	1	1	1
Term.setCoef(BigInteger)	1	1	1
Term.setXexpo(BigInteger)	1	1	1
Term.toString()	8	12	18
Term.trilistequals(ArrayList<Trifact>)	5	5	10
Tree.Tree(TreeNode)	1	1	1
Tree.derivetree()	1	1	1
Tree.getRoot()	1	1	1
TreeNode.TreeNode(Alpha)	1	1	1
TreeNode.clone()	1	3	3
TreeNode.derive(TreeNode)	8	8	12
TreeNode.getAlpha()	1	1	1
TreeNode.getLeftchild()	1	1	1
TreeNode.getRightchild()	1	1	1
TreeNode.getexp(TreeNode)	1	15	17
TreeNode.isroot()	1	1	1
TreeNode.setLeftchild(TreeNode)	1	1	1
TreeNode.setRightchild(TreeNode)	1	1	1
TreeNode.setroot()	1	1	1
Trifact.Trifact(String,BigInteger,Expre)	1	1	1
Trifact.clone()	1	1	1
Trifact.equals(Trifact)	4	1	4
Trifact.getExp()	1	1	1
Trifact.getExpo()	1	1	1
Trifact.getId()	1	1	1
Trifact.setExpo(BigInteger)	1	1	1
Trifact.toString()	3	2	5

bug分析：

本次作业的bug集中出现在最后的化简合并当中， 强测发现了以下bug：合并当中把sin（0）当做1，比较两个表达式是否相同的过程中出现了bug，这表明在完成作业后的测试工作不到位，一些较少出现的情况中的bug未能覆盖到。在互测阶段同样有同样的问题，构造的情况较少，不够复杂，没有覆盖到各种情况，导致查找bug的结果不理想。

总结：

这是第一单元的最后一次作业，复杂度比第二次作业提升了很多，由于在第二次作业中完成了树的主体的构建，本次作业主要精力放在了输入和化简输出上，尽管如此在化简过程中仍产生了大量的bug，在以后的作业中需要构造自动测试程序完成自动化测试。另外，本次作业再次印证了层次结构对程序的重要性，若能把层次划分得当，在调试和后续的扩展都能省不少力气。