2-SAT

by a1a2a3a4a5

定义

k−SAT：“k-适应性问题”，基本是这样的：

给你 n 个 bool 变量，同时还有一些约束，问是否有一种取值方式满足所有的约束。

“约束”和“满足”的解释如下，其中括号里是“约束”，括号外的 \(∧\) 是“满足”：

• 当 k = 2 时，使 \((¬a∨b)∧(a∨b)∧(¬a∨¬b) = 1\)。
• 当 k = 3 时，使 \((¬a∨b∨¬c)∧(a∨b∨¬c)∧(¬a∨¬b∨c) = 1\)。
• 以此类推

k > 3 ：我不会，已被证明为 NP 完全 的，只能暴力。

k = 1：这个全赋成 1 就完了。

k = 2：有点意思，所以只有 2-sat 需要学。

建图

一个有向边代表一个“可推”，我们把每个变量拆成 true 点和 false 点。

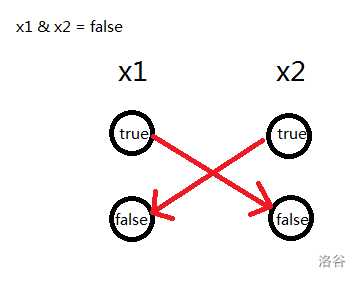
在上图中其中一个不成立则另一个一定成立，其他类型的约束需要另行考虑。

判无解

如果两个点属于同一个变量还在同一个强连通分量里，使用 tarjan 判断。

赋值

我们发现，从 \(x_1\) 的 false 出发会走到 \(x_1\) 的 true ，也就是说 \(x_1\) 现在只能等于 true 了；同理从 \(x_2\) 的 true 出发能走到 \(x_2\) 的 flase，说明 \(x_2\) 只能等于 flase；

我们要在两种取值中选择拓扑序较大的那个值。（这是保证不会错的，因为有时候两个值取哪个都行）

其实我们在 Tarjan 的时候就已经求出了强联通分量的拓扑序了，只不过是反序。

（强联通分量的拓扑序越小，被缩得越早，越晚被搜索树遍历，因为他是个栈）

代码实现

P4782 【模板】2-SAT

#include<bits/stdc++.h>
#define ovo 2100000
using namespace std;
bool zai[ovo];
int head[ovo],cnt,dfn[ovo],low[ovo],kuai[ovo],k;
struct xxx {int v,xia;} e[ovo],g[ovo];
void add(int u,int v) {e[++cnt].v=v,e[cnt].xia=head[u],head[u]=cnt;}
int zhan[ovo],top;
void tajian(int u)
{
	dfn[u]=++cnt;low[u]=cnt;
	zhan[++top]=u;zai[u]=1;
	for(int i=head[u];i;i=e[i].xia)
	{
		int v=e[i].v;
		if(!dfn[v]) tajian(v),low[u]=min(low[u],low[v]);
		else if(zai[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u])
	{
		k++;
		while(zhan[top]!=u) zai[zhan[top]]=0,kuai[zhan[top]]=k,top--;
		kuai[u]=k,zai[u]=0;top--;
	}
}

int n,m;
int main()
{
	cin>>n>>m;
	for(int i=1,o1,o2,x,y;i<=m;i++)
	{
		cin>>o1>>x>>o2>>y;
		if(x==0&&y==0) add(o1+n,o2),add(o2+n,o1);
		else if(x==0&&y==1) add(o1+n,o2+n),add(o2,o1);
		else if(x==1&&y==0) add(o1,o2),add(o2+n,o1+n);
		else if(x==1&&y==1) add(o1,o2+n),add(o2,o1+n);
	}
	for(int i=1;i<=2*n;i++) if(!dfn[i]) tajian(i);
	for(int i=1;i<=n;i++) if(kuai[i]==kuai[i+n]) return puts("IMPOSSIBLE"),0;
	puts("POSSIBLE");
	for(int i=1;i<=n;i++) cout<<((kuai[i]>kuai[i+n])?"1 ":"0 ");
	return 0;
}