宽搜+A*+IDA*

\(BFS\) · 宽度优先搜索/广度优先搜索

一般基于队列实现

主要步骤 :

1. 起点入队列
2. 进行扩展（包括边界的判断 , 是否已经走过这个点）
3. 达到目标退出

伪代码：

int dx[5]={-1,0,1, 0};
int dy[5]={ 0,1,0,-1};
vis[x][y]=true;
q.push(make_pair(x,y));
while(!q.empty()) {
	int xx=q.front().first,yy=q.front().second;
	q.pop();
	for(int i=0;i<4;i++) {
		int fx=x+dx[i],fy=yy+dy[i];
		if(fx<1||fx>n||fy<1||fy>m||vis[fx][fy])
		    continue;
	    vis[fx][fy]=true;
		q.push(make_pair(fx,fy));
		f[fx][fy]=f[xx][yy]+1；
    }

例题

${\color{Blue} \mathbb{普及-/提高+} } $

ti

题目描述

在一个大小为n*n的棋盘上有一个马。无限次数地可以完成特定的动作。

每一种动作包含两个整数，第一个数说明上下移动的数，第二个数说明左右移动的数，来说明这个动作。（正数向右，负数向左）

看是否可以到达棋盘上的每一个地方。（棋盘无限大）

输入格式

第一行中存在一个整数 \(T\)，表示数据组数。

对于每一组数据，第一行一个数 \(N\)，表示超级马能完成的动作个数。

接下来 \(N\) 行，每一个行中包含两个整数 \(P\) 和 \(Q\)，表示这个动作。

输出格式

输出 \(K\) 行，判断超级马是否可以到达棋盘所有地方，可以输出 TAK，否则输出 NIE。

样例输入 #1

2
3
1 0
0 1
-2 -1
5
3 4
-3 -6
2 -2
5 6
-1 4

样例输出 #1

TAK
NIE

数据范围：\(1 \le K,N \le 100,-100 \le P,Q \le 100,n \le 10000000\)。

---

---

\(A*\)

one of 启发式搜索

基于\(BFS\) 实现是\(BFS\) de 优化

使用启发式函数来估计从当前节点到目标节点的距离，从而优化搜索路径。

主要部分是估价函数 \(f(x) = g(x) + h(x)\)

\(g(x)\) 表示从初始状态到当前状态的花费/距离

\(f(x)\) 表示从当前状态到最终状态的花费/距离

例题

ti

题目描述

\(N\) 为贝西所在的牛棚（最高点），\(1\) 为池塘（最低点）。

比如说，她希望能有 \(K\) 种不同的路线。同时，为了避免跑得太累，她希望这 \(K\) 条路线是从牛棚到池塘的路线中最短的 \(K\) 条。如果两条路线包含的道路组成的序列不同，则这两条路线被认为是不同的。

将牧场网络里最短的 \(K\) 条路径的长度分别算出来。你将会被提供一份牧场间路线的列表，每条道路用 \((X_i, Y_i, D_i)\) 表示，意为从 \(X_i\) 到 \(Y_i\) 有一条长度为 \(D_i\) 的道路。

输入格式

第一行三个用空格分开的整数 \(N,M,K\)，其中 。

第二行到第 \(M+1\) 行每行有三个用空格分开的整数 \(X_i,Y_i,D_i\)，描述一条下坡的道路。

输出格式

共 \(K\) 行，在第 \(i\) 行输出第 \(i\) 短的路线长度，如果不存在则输出 \(-1\)。如果出现多种有相同长度的路线，务必将其全部输出。

数据规模与约定

对于全部的测试点，保证 \(1 \le N \le 1,000\)，\(1 \le M \le 1\times10^4\)，\(1 \le K \le 100\)，\(1 \le Y_i < X_i\le N\)，\(1 \le D_i \le 1\times 10^6\)，

\(IDA*\)

one of 启发式搜索

基于\(DFS\) 实现是\(DFS\) de 优化

是 迭代加深 的思想与 估价函数 的 \(有机结合\)

\(DFS + 估价函数 \stackrel{迭代加深}{\longrightarrow} IDA*\)

\(IDA*\) 可以有效防止DFS爆栈，减小空间消耗

例题

题目描述

输入格式

第一行有一个正整数 \(T\)（\(T \le 10\))，表示一共有 \(T\) 组数据。

接下来有 \(T\) 个 \(5 \times 5\) 的矩阵，0 表示白色骑士，1 表示黑色骑士，* 表示空位。两组数据之间没有空行。

输出格式

对于每组数据都输出一行。如果能在 \(15\) 步以内（包括 \(15\) 步）到达目标状态，则输出步数，否则输出 -1。

样例输入 #1

2
10110
01*11
10111
01001
00000
01011
110*1
01110
01010
00100

样例输出 #1

7
-1

提示

P2534

题目描述

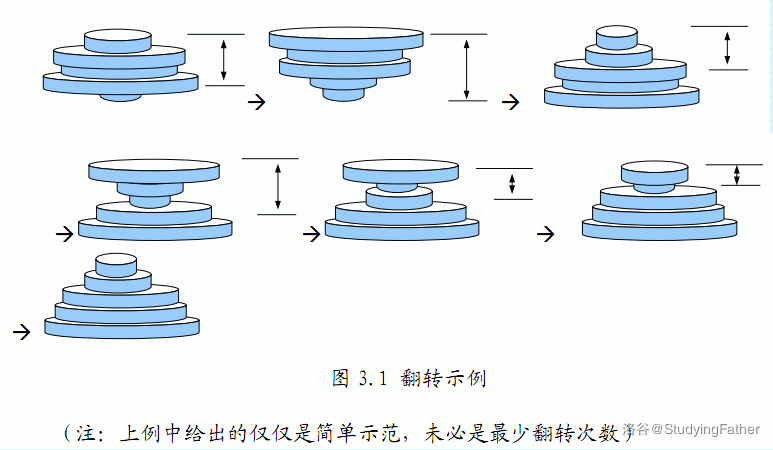
在训练中，一些臂力训练器材是少不了的，小龙在练习的时候发现举重器械上的铁盘放置的非常混乱，并没有按照从轻到重的顺序摆放，这样非常不利于循序渐进的锻炼。他打算利用一个非常省力气的办法来整理这些铁盘，即每次都拿起最上面的若干个圆盘并利用器械的力量上下翻转，这样翻转若干次以后，铁盘将会按照从小到大的顺序排列好。那么你能不能帮小龙确定，最少翻转几次就可以使铁盘按从小到大排序呢？

例如：下面的铁盘经过如图所示的以下几个步骤的翻转后变为从小到大排列。

输入格式

共两行。第一行为铁盘个数 \(N\)（\(1 \leq N \leq 16\)），第二行为 \(N\) 个不同的正整数，分别为从上到下的铁盘的半径 \(R\)（\(1 \leq R \leq 100\)）。