Loading

随机化算法

random

一些随机函数

1

\(rand()\)

很常用但是只可以生成\([0,32767]\)的整数值域较小


#include<bits/stdc++.h>
using namespace std;
int main() {
	srand(time(0));
	cout<<rand();
    return 0;
}

2

\(mt19937\)
可以生成\(unsigned\) \(int\) 内的整数值域较大


#include <ctime>
#include <iostream>
#include <random>
using namespace std;
int main() {
    mt19937 myrand(time(nullptr));
    cout << myrand() << endl;
    return 0;
}

随机算法

1.爬山算法

单峰函数上的求解

对于单峰函数上的求解问题，我们可以选定一个初始答案，然后随机往左右两侧跳，比较新的答案与现在的答案对应函数值的大小关系。若新的答案更优，则跳到新的答案处。在更新的过程中，我们逐步减小随机跳的范围，当范围足够小时停止操作，则那个时候的答案就是最终的答案。而在整个过程中，随机范围的减小就对应着温度的降低。这个过程类似于往上爬山，故称之为“爬山算法”。

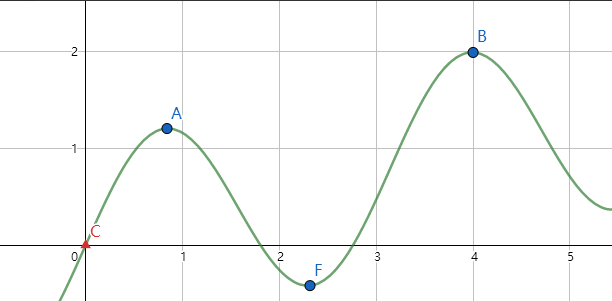
如图，由\(C\)点出发就会陷入\(A\)点的局部最优解，
一看就不对。

所以，我们的模拟退火就应运而生了（赏析本段的作用）

2.模拟退火

对多峰下爬山的正确率优化

如同前面所说的，每随机到一个答案，我们就与现目前的最优答案进行比较。若新的答案更优，我们直接取新的答案；否则我们以一定的概率，跳到最新的答案上去，但最优答案仍然不变。随着温度的降低，我们逐步锁定了最优的峰，此时跳到较劣答案上的概率应当降低（注意：此时的答案范围不一定必要缩小）。此外，较劣答案与最优答案的函数值之差越大，跳到较劣答案上的概率也应当越低。

我们可以用函数求得上述函数值，即


p=exp(-x/temp);

求得概率后，我们可以通过随机一个\([0,1]\)范围内的实数，并比较它与概率值的大小，确定是否跳到较劣答案上去。求随机实数可以写作


(double)rand()/1.0/RAND_MAX。

实现与爬山算法基本类似，只需要多加上跳到较劣答案上的判断即可。

简单来说,只需要在选择进不进行行动时把这个粘上去就行


if(k<now||(exp((ans-k)/i) > (db)(rand())/RAND_MAX){
    //这里放更新状态
}

显然在考场上还要进行必要的时间复杂度计算;

当然也可进行代码内的时间计数

例题

这里就有入问了：

主播，主播

平衡点 / 吊打XXX

确实很好但还是太水了，有没有一些更强势的例题

有的，兄弟，有的，这样的题当然不只一道了，这样强势的题一共还有九道，都是版本\(T0.5\)强度的题目：

posted @ 2025-03-12 16:09  dfgz  阅读(42)  评论(0)    收藏  举报