【洛谷】【扩欧】P1516 青蛙的约会

【题目描述】

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。

我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。

【输入格式】

 输入只包括一行5个整数x，y，m，n，L

其中0<x≠y < =2000000000，0 < m、n < =2000000000，0 < L < =2100000000。

 【输出格式】

输出碰面所需要的天数，如果永远不可能碰面则输出一行"Impossible"。

 

【算法分析：】

设最少需要的次数为k，容易得出：

求一个非负整数k，使得：

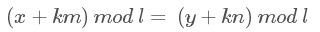
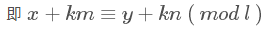
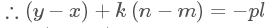
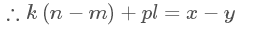
可以看出，问题变成了求不定方程的x的非负最小值

 

求出一组x、y，使得ax+by=gcd(a,b):

ax + by = gcd(a, b)
    = gcd(b, a % b)
    = bx' + (a % b)y'
    = bx' + (a - [a / b] * b)y'
    = bx' + ay' - [a / b] * by'
    = ay' + b(x' - [a / b]y')
    
∴x = y', y = x' - [a / b] * y'

终止条件：
b = 0时：a * 1 + b * 0 = a
即x = 1, y = 0
递归求解

 

求出一组ax+by=c的解：

用扩展欧几里得先求出ax' + by' = gcd(a, b)的一组解, x',  y'及gcd(a, b)的值

若c mod gcd(a, b) ≠ 0
方程无解（整数范围内）

令：
c = gcd(a, b) * k
∴k = c / gcd(a, b)
∴ax + by = c
      = k * gcd(a, b)
∴ax + by = akx' + bky'
根据恒等定理：
    ax = akx', by = bky'
∵a != 0 且 b != 0
∴x = kx', y = ky'
∵k = c / gcd(a, b)
∴x = x' * c / gcd(a, b)
  y = y' * c / gcd(a, b)

 

使得x非负且最小：

用扩展欧几里得先求出ax' + by' = gcd(a, b)的一组解, x',  y'及gcd(a, b)的值
lcm(a, b) = a * b / gcd(a, b)

ax + lcm(a, b) + by - lcm(a, b) = c
ax + a * b / gcd(a, b) + by - a * b / gcd(a, b) = c
a(x + b / gcd(a, b)) + b(y - a / gcd(a, b)) = c
∴x + 或 - 任意倍数的b / gcd(a, b)均有对应的y的整数解

设 t = b / gcd(a, b)
x = ((x' * c / gcd(a, b)) % t + t) % t 为方程的最小非负解.

扩欧代码及详解见我的github:
DEVILK1

 

【代码：】

 

#include<iostream>
#include<cstdio>
using namespace std;

int x, y, m, n, l;

int read() {
    int x = 0, f = 1; char ch = getchar();
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
        x = (x << 1) + (x << 3) + (ch ^ 48),
        ch = getchar();
    return x * f;
}

int ex_gcd(int a, int b, int &x, int &y) {
    if(b == 0) {
        x = 1, y = 0;
        return a;
    }
    int g = ex_gcd(b, a % b, y, x);
    y -= a / b * x;
    return g;
}

int main() {
    x = read(), y = read();
    m = read(), n = read();
    l = read();
    int a = n - m, c = x - y;
    if(a < 0) a = -a, c = -c;
    int x0, y0;
    int g = ex_gcd(a, l, x0, y0);
    if(c % g != 0) {
        puts("Impossible");
        return 0;
    }
    int t = l / g;
    x0 = ((1LL * x0 * c / g) % t + t) % t;
    cout << x0 << endl;
}