Demonic Theorem
先来观察几组数据:
先将1~10这10个自然数进行二次方运算,然后再依次从下向上减,最终总会得到0,倒数第二步是2;接着,若将这些数三次方后再依次从下向上减,第三步会得到0,倒数第二步是6;若将这些数四次方后再依次从下向上减,第三步会得到0,倒数第二步是24;若将这些数五次方后再依次从下向上减,第三步会得到0,倒数第二步是120;也许你会注意到:2!=2 3!=6 4!=24 5!=120
我把它归纳为定理一(Demonic Theorem 1#):
若将自然数的n次方从大到小依次相减,再将他们的差依次相减……则在第(n+1)步得到0,第n步得到n!(n>=2)。
随后我发现当n=0和n=1时,上述定理同样成立:
若将定理一进行推广可从两方面进行考虑:一是从所取数字集合的范围上考虑,定理一中的自然数是否可以修正为所有整数呢?以n=3和n=4为例:
可见在整数范围内都符合;二是从所取数字集合的性质上考虑,连续整数可以看做是公差为1的等差数列,是否可以推广为公差为任意整数d的等差数列呢?以n=3,d=3和n=4,d=3为例,此时第n步得到的数字是什么呢?
将定理一推广后,第n步得到的数字将与d有关,而162和1944和3有什么关系呢?观察后不难发现如下关系:
162=3!33=n!dn 1944=4!34=n!dn
由此定理一被推广为定理二(Demonic Theorem 2#):
定义在Z上的任一等差数列{am}按一定顺序(从大到小或从小到大)排列起来并进行n次方运算,然后按从大到小的顺序依次相减,再将所得的差依次相减……在第n步得到n!dn(d为{am}的公差),第(n+1)步得到0。
(注:当n=2k-1(k为自然数)时,第(n-1)步所对应的数字为amn!d(n-1);当n=2k(k为自然数)时,第(n-1)步所对应的数字为An!d(n-1)(A=(am+a(m-1))/2,A为其所在行对应的数字位置相邻两数的等差中项);
最后,给出一个该定理的图例,根据二项式定理展开后的表达也许更清楚的诠释了这个定理的内在本质:
(注1:这个定理是十几年前在初中数学的学习过程中得到的,现更新至博客,本问中的定理为孩童时代的戏称,不代表任何官方定理)
(注2:本文系孩童时代研究费马大定理即xn+yn=zn(n>2)无正整数解的产物,我依然坚信这个定理象费马“猜想”的那样有更简单的证明)
转载请遵循此协议:署名 - 非商业用途 - 保持一致

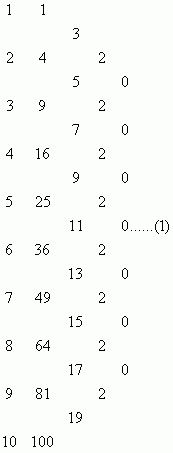


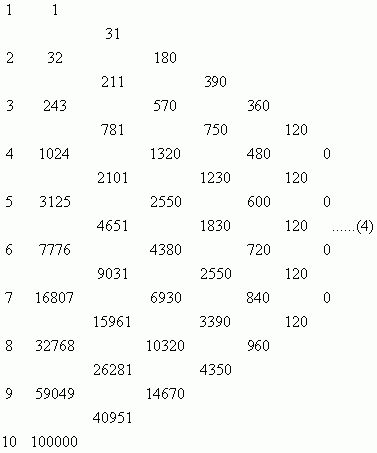
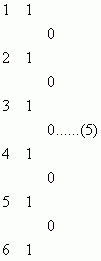
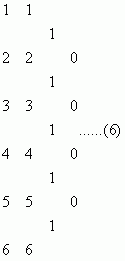
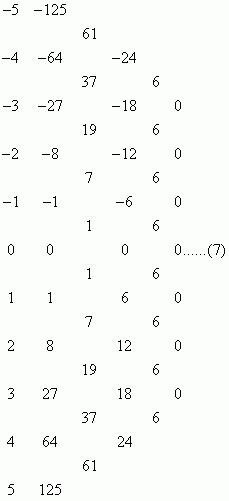
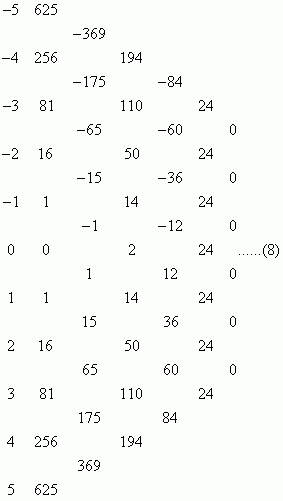
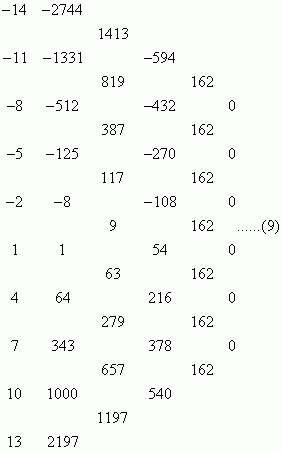
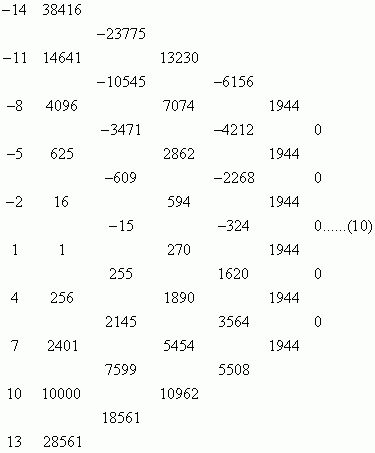
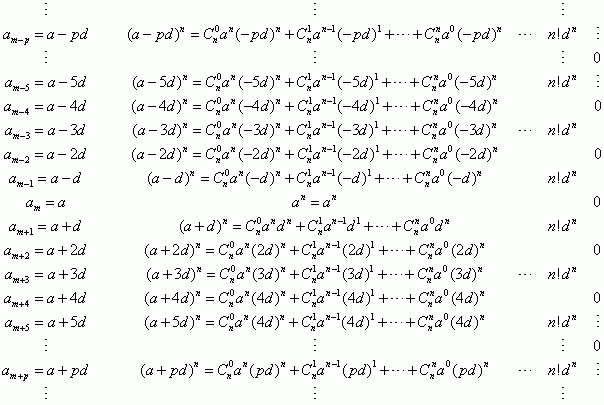

 浙公网安备 33010602011771号
浙公网安备 33010602011771号