shr讲座 - Z 函数（扩展KMP）

定义

字符串 \(S\) 的 Z 函数是一个长度为 \(|S|\) 的数组。\(f_i\) 表示 \(S_{i...|S|}\) 与 \(S\) 的最长公共前缀。

注意 \(f_1=|S|\)

求法

参考 KMP 的思想。我们想要从已知的信息中推出未知的信息。

过程

我们先记录一个 \(k\)，初始为 \(0\)，表示除了 \(1\) 的 \(pos+f_{pos}-1\) 最大的 \(pos\)。依次对于每个 \(i=2,3,\dots,n\) 求 \(z_i\)，分两种情况讨论：

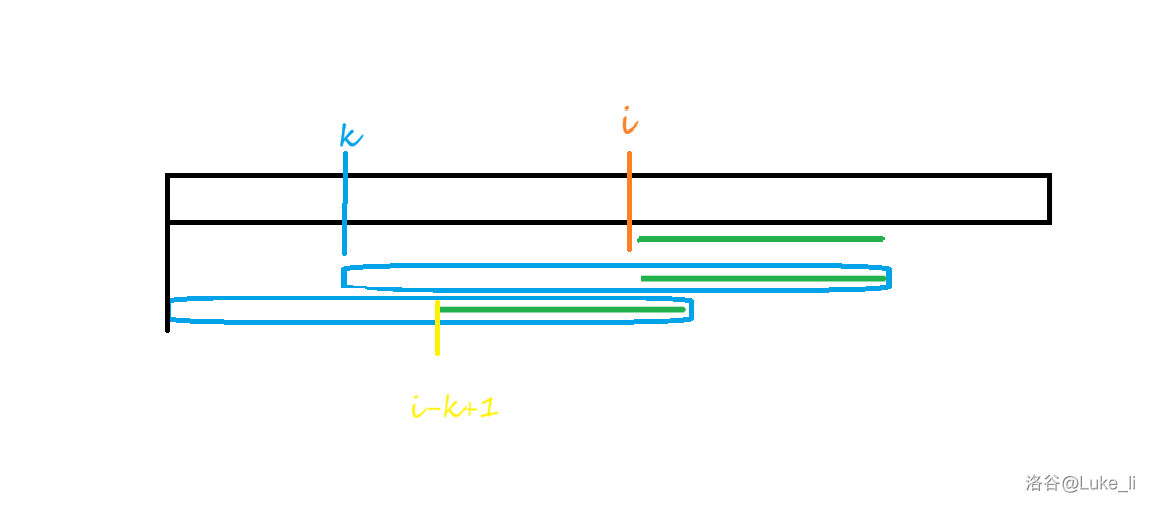
• 如果 \(k+f_k-1\ge i\)，那么如图所示。蓝色线段代表 \(k\) 位置的后缀对应的 LCP，显然图中所有绿色线段对应的字符串是相等的。由于 \(i-k+1\) 位置的后缀和 \(i\) 位置的后缀具有相同前缀，我们可以借用 \(f_{i-k+1}\) 的值。

  具体而言，就是令 \(f_{i}\leftarrow \min(k+f_k-i,f_{i-k+1})\)（\(\min\) 前半部分的式子是绿色段的长度，因为我们不知道绿色段之后二者是否一样，所以要截断嘛）。之后我们暴力增加 \(f_i\) 即可。
  

• 如果 \(k+f_k-1< i\)，从 \(0\) 开始暴力增加 \(f_i\) 即可。

• 最后别忘了更新 \(k\)。

复杂度为什么是对的呢？

参考 manacher 的复杂度证明。

对于第一种情况，分两类：如果 \(f_i\) 被截断到了绿色段的长度，那么 \(i+f_i-1\) 就触及了右边界，此时每次f[i]++ 都是在拓宽我们的右边界；如果 \(f_i\) 没有抵达绿色段的长度，显然 \(f_i\) 已经到头了，不会再增长。由于右边界只会拓宽 \(n\) 次，复杂度是 \(O(n)\) 的。

对于第二种情况，哪怕 \(f_i=0\) 也必然有 \(i+f_i-1>k+f_k-1\)，也就是说每一次 f[i]++ 都是在拓宽我们的右边界，同理第一种情况，均摊下来就是 \(O(n)\) 的。

请注意，初始化时不能令 \(k=1\)，否则始终有 \(k+f_k-1=n\ge i\)，而 \(i-k+1=i\)，但是我们还没有求出 \(f_i\) 的值，这会产生错误或者让算法退化到 \(O(n^2)\)。所以建议初始化时令 \(k=0,f_0=0\)，避免这一问题。

模板题 代码

第二问我是把 b 和 a 拼接起来，并在中间加一个分隔符实现的。实现上有点劣，但是无伤大雅，反正时空复杂度没什么区别。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=2e7+10;
ll n;
ll f[N*2],k;
char s[N*2],a[N],b[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>(a+1)>>(b+1);
    ll la=strlen(a+1),lb=strlen(b+1);
	for(ll i=1;i<=lb;i++)
		s[i]=b[i];
	s[lb+1]=' ';
	for(ll i=1;i<=la;i++)
		s[i+lb+1]=a[i];
	n=strlen(s+1);
	
	k=0;
	f[1]=n;
	for(ll i=2;i<=n;i++)
	{
		if(k+f[k]-1>=i)
			f[i]=min(k+f[k]-i,f[i-k+1]);
		else
			f[i]=0;
		while(i+f[i]<=n && s[f[i]+1]==s[i+f[i]])
			f[i]++;
		if(k+f[k]-1<i+f[i]-1)
			k=i;
	}
	
	ll ans1=0,ans2=0;
	for(ll i=1;i<=lb;i++)
	{
		ans1^=i*(min(f[i],lb-i+1)+1);
	}
	for(ll i=lb+2;i<=n;i++)
	{
		ans2^=(i-lb-1)*(f[i]+1);
	}
	cout<<ans1<<endl<<ans2<<endl;
    return 0;
}

应用

查找在 B 中 A 出现了几次

把 A 和 B 拼在一起，中间加一个分隔符（如*），然后求 Z 函数。在 B 字符串范围内的每有一个 \(f_i>=|A|\) 就说明 A 出现了一次。时间复杂度 \(O(|A|+|B|)\)