[离散数学]集合3.7

第三章 集合与关系

3.7 复合关系和逆关系

1. 复合关系

2. 逆关系

1 复合关系

定义:3-7.1：设R是X到Y的二元关系，S为Y到Z的二元关系，则R◦S称为R和S的复合关系，表示为：

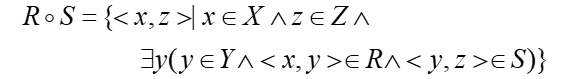
例题：

1.集合运算求法

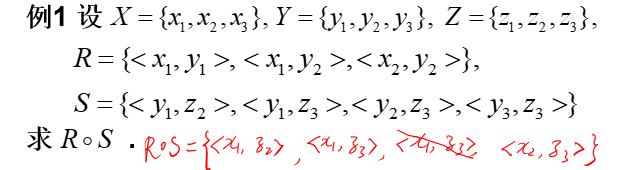
（即：若R中某序偶的值域与S中某序偶的前域相同，则用该R中序偶的前域与S中序偶的值域组成新的序偶，放入集合R◦S中）

2.矩阵运算求法

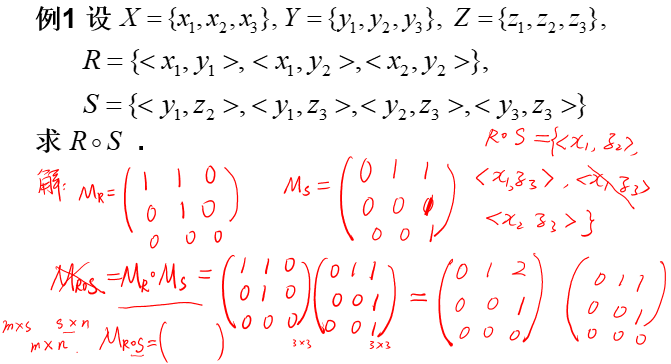
求两关系的复合关系可用矩阵乘法实现，将乘积的结果矩阵中非0元素都改为1即得到原来两关系的复合关系。（例如上图中乘出来的结果矩阵含有2，则将2改为1）

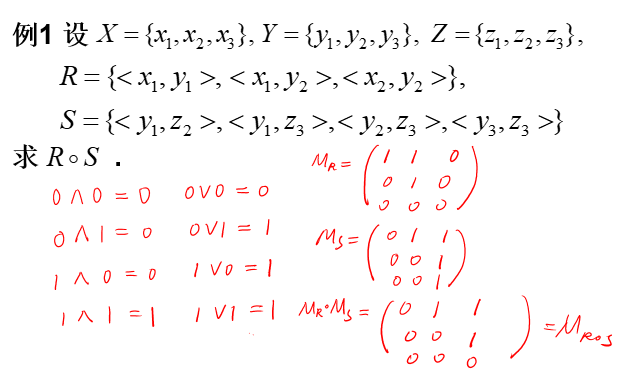
3.关系图求法

也可用矩阵的逻辑乘运算实现，上图中 ∧ 表示矩阵元素的逻辑乘，类似于集合的 ∩，命题逻辑的 合取 连接词，同理 **∨ ** 表示矩阵元素的逻辑加，类似于集合的 ∪，命题逻辑的 析取联结词，矩阵的逻辑乘运算将矩阵乘法中执行的加法用逻辑加替换，乘法用逻辑乘替换。

复合关系也可由关系图的表示求得：

描述法表示的复合关系求法：

关系的复合运算满足结合律，命题如下:

证明思路：用集合相等的证明方法，证明从左边集合中任取一个元素，都会在右边集合中出现，从而证明左边⊆右边，同理：可证明右边⊆左边，进而证明了两边相等。

规定：当R是X上的复合关系时有：

1. R的0次幂为恒等关系
2. R的平方表示R和R自己作关系复合运算 R◦R
3. R的n+1次方是R的n次方和R作关系复合运算

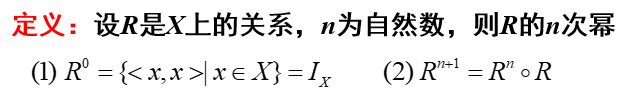
2 逆关系

逆关系对应的矩阵运算为矩阵转置

复合关系T◦S整体求逆关系 也类似于 矩阵AB整体求转置

（反对称关系要求：可以有<1,1>、<2,2>、<4,4>这种，但如果有<1,2>就不能有<2,1>，有<2,3>就不能有<3,2>，这样一来，反对称关系 和 它的逆关系 做交集运算就只能保留属于恒等关系的那一部分的元素了，所以它们的交集是恒等关系的子集，对应到矩阵运算中是只保留主对角线上的元素）