优化库之-----Ceres库学习笔记(一)
Ceres解决的是非线性优化问题,给定初值,得出最优解, 主要在SLAM中使用。
一般的可求解形如下面的最小二乘优化问题:
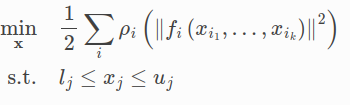
例如求解![]() 最小值,本文后续以求解该例为主线。
最小值,本文后续以求解该例为主线。
Ceres的使用流程是:
建立仿函数,定义变量并初始化,建立优化问题,建立CostFunction,求解.
1. 建立仿函数
先在头文件书写一个类,定义残差的表达方式。这个类的书写方式采用仿函数的方法,仿函数(Functor)也叫函数对象,顾名思义就是让一个类用的时候像函数一样方便。
仿函数的简单示例code-A:
class A{ public: bool operator () (int num){ if(num>0){cout<<"positive!"<<endl;return 1;} else {cout<<"negative!"<<endl;return 0;} } }; int main(int argc, char**argv){ A a; a(-10);//是不是感觉很方便 }
更进一步,在Ceres中的用法code-B:
struct CostFunctor { template <typename T> bool operator()(const T* const x, T* residual) const { residual[0] = 10.0 - x[0]; return true; } };
在Vins_fusion中是这样用的code-C:
struct TError { TError(double t_x, double t_y, double t_z, double var) //TError类的构造函数,包括x,y,z三维坐标,与位置精度var; :t_x(t_x), t_y(t_y), t_z(t_z), var(var){} template <typename T> bool operator()(const T* tj, T* residuals) const //模板仿函数类定义,与code-A中的仿函数一样,区别是此处函数参数为模板类T. { residuals[0] = (tj[0] - T(t_x)) / T(var); residuals[1] = (tj[1] - T(t_y)) / T(var); residuals[2] = (tj[2] - T(t_z)) / T(var); return true; } ....... };
2. 定义优化变量并初始化
double initial_x = -255.0; // The variable to solve for with its initial value. double x = initial_x;
3. 建立优化问题
Problem problem; // Build the problem.
4. 建立CostFunction
CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor); //使用AutoDiffCostFunction,另外可用的还有NumericDiffCostFunction,Analytic Derivatives.官方推荐使用AutoDiffCostFunction problemA.AddResidualBlock(cost_function, nullptr, &x); //<CostFunctor, 1, 1>两个参数的含义,输出维度与输入维度,输出维度是残差residual维度,输入维度是优化变量x维度.
5. 求解
Solver::Options options; //求解器参数设置 options.linear_solver_type = ceres::DENSE_QR; //线性求解器类型设置,Ceres的线性求解器类型有,DENSE_QR,DENSE_NORMAL_CHOLESKY,SPARSE_NORMAL_CHOLESK,CGNR,DENSE_SCHUR,SPARSE_SCHU,ITERATIVE_SCHUR options.minimizer_progress_to_stdout = true; //将求解迭代过程用cout打印出来 Solver::Summary summary; Solve(options, &problem, &summary); //标准的求解语句 std::cout << summary.BriefReport() << "\n"; //打印求解结果
接下来用两个案例说明完整过程
案例1:
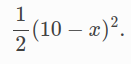
案例2:
vins_fusion的位姿优化
案例1:
struct CostFunctor { template <typename T> bool operator()(const T* const x, T* residual) const { residual[0] = 10.0 - x[0]; return true; } }; int main(int argc, char** argv) { google::InitGoogleLogging(argv[0]); // The variable to solve for with its initial value. double initial_x = 5.0; double x = initial_x; // Build the problem. Problem problem; // Set up the only cost function (also known as residual). This uses // auto-differentiation to obtain the derivative (jacobian). CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor); problem.AddResidualBlock(cost_function, nullptr, &x); // Run the solver! Solver::Options options; options.linear_solver_type = ceres::DENSE_QR; options.minimizer_progress_to_stdout = true; Solver::Summary summary; Solve(options, &problem, &summary); std::cout << summary.BriefReport() << "\n"; std::cout << "x : " << initial_x << " -> " << x << "\n"; return 0; }
newGPS = false; printf("global optimization\n"); TicToc globalOptimizationTime; ceres::Problem problem; ceres::Solver::Options options; options.linear_solver_type = ceres::SPARSE_NORMAL_CHOLESKY; //options.minimizer_progress_to_stdout = true; //options.max_solver_time_in_seconds = SOLVER_TIME * 3; options.max_num_iterations = 5; ceres::Solver::Summary summary; ceres::LossFunction *loss_function; loss_function = new ceres::HuberLoss(1.0); ceres::LocalParameterization* local_parameterization = new ceres::QuaternionParameterization(); //add param mPoseMap.lock(); int length = localPoseMap.size(); // w^t_i w^q_i double t_array[length][3]; double q_array[length][4]; map<double, vector<double>>::iterator iter; iter = globalPoseMap.begin(); for (int i = 0; i < length; i++, iter++) { t_array[i][0] = iter->second[0]; t_array[i][1] = iter->second[1]; t_array[i][2] = iter->second[2]; q_array[i][0] = iter->second[3]; q_array[i][1] = iter->second[4]; q_array[i][2] = iter->second[5]; q_array[i][3] = iter->second[6]; problem.AddParameterBlock(q_array[i], 4, local_parameterization); problem.AddParameterBlock(t_array[i], 3); } map<double, vector<double>>::iterator iterVIO, iterVIONext, iterGPS; int i = 0; for (iterVIO = localPoseMap.begin(); iterVIO != localPoseMap.end(); iterVIO++, i++) { //vio factor iterVIONext = iterVIO; iterVIONext++; if(iterVIONext != localPoseMap.end()) { Eigen::Matrix4d wTi = Eigen::Matrix4d::Identity(); Eigen::Matrix4d wTj = Eigen::Matrix4d::Identity(); wTi.block<3, 3>(0, 0) = Eigen::Quaterniond(iterVIO->second[3], iterVIO->second[4], iterVIO->second[5], iterVIO->second[6]).toRotationMatrix(); wTi.block<3, 1>(0, 3) = Eigen::Vector3d(iterVIO->second[0], iterVIO->second[1], iterVIO->second[2]); wTj.block<3, 3>(0, 0) = Eigen::Quaterniond(iterVIONext->second[3], iterVIONext->second[4], iterVIONext->second[5], iterVIONext->second[6]).toRotationMatrix(); wTj.block<3, 1>(0, 3) = Eigen::Vector3d(iterVIONext->second[0], iterVIONext->second[1], iterVIONext->second[2]); Eigen::Matrix4d iTj = wTi.inverse() * wTj; Eigen::Quaterniond iQj; iQj = iTj.block<3, 3>(0, 0); Eigen::Vector3d iPj = iTj.block<3, 1>(0, 3); ceres::CostFunction* vio_function = RelativeRTError::Create(iPj.x(), iPj.y(), iPj.z(), iQj.w(), iQj.x(), iQj.y(), iQj.z(), 0.1, 0.01); problem.AddResidualBlock(vio_function, NULL, q_array[i], t_array[i], q_array[i+1], t_array[i+1]); }
//gps factor double t = iterVIO->first; iterGPS = GPSPositionMap.find(t); if (iterGPS != GPSPositionMap.end()) { ceres::CostFunction* gps_function = TError::Create(iterGPS->second[0], iterGPS->second[1], iterGPS->second[2], iterGPS->second[3]); //printf("inverse weight %f \n", iterGPS->second[3]); problem.AddResidualBlock(gps_function, loss_function, t_array[i]); } } //mPoseMap.unlock(); ceres::Solve(options, &problem, &summary); std::cout << summary.BriefReport() << "\n"; // update global pose //mPoseMap.lock(); iter = globalPoseMap.begin(); for (int i = 0; i < length; i++, iter++) { vector<double> globalPose{t_array[i][0], t_array[i][1], t_array[i][2], q_array[i][0], q_array[i][1], q_array[i][2], q_array[i][3]}; iter->second = globalPose; if(i == length - 1) { Eigen::Matrix4d WVIO_T_body = Eigen::Matrix4d::Identity(); Eigen::Matrix4d WGPS_T_body = Eigen::Matrix4d::Identity(); double t = iter->first; WVIO_T_body.block<3, 3>(0, 0) = Eigen::Quaterniond(localPoseMap[t][3], localPoseMap[t][4], localPoseMap[t][5], localPoseMap[t][6]).toRotationMatrix(); WVIO_T_body.block<3, 1>(0, 3) = Eigen::Vector3d(localPoseMap[t][0], localPoseMap[t][1], localPoseMap[t][2]); WGPS_T_body.block<3, 3>(0, 0) = Eigen::Quaterniond(globalPose[3], globalPose[4], globalPose[5], globalPose[6]).toRotationMatrix(); WGPS_T_body.block<3, 1>(0, 3) = Eigen::Vector3d(globalPose[0], globalPose[1], globalPose[2]); WGPS_T_WVIO = WGPS_T_body * WVIO_T_body.inverse(); } } updateGlobalPath(); //printf("global time %f \n", globalOptimizationTime.toc()); mPoseMap.unlock();
另外在SLAM中BA问题是一个基础问题,BA全拼是Bundle Adjustment ,译为光束法平差,BA的本质是一个优化模型,目的是最小化重投影误差。经典文献 Bundle Adjustment——A Mordern Synthsis



 浙公网安备 33010602011771号
浙公网安备 33010602011771号