红黑数学习笔记
红黑树介绍
红黑数一种为了实现平衡二叉树的数据结构(因为二叉树在最坏的情况下时间复杂度等于线性的复杂度),红黑数的时间复杂度O(lgn),最坏情况也是如此。
红黑书需要满足五点性质:
1.所有节点只能是黑色或者红色
2.根结点必定为黑色
3.所有叶子节点(NIL或者null)必为黑色
4.红节点的子节点必为黑色
5.树种任意的一个节点到其所有叶子的节点的路径黑色节点的数量都是一样的
红黑树示意图:
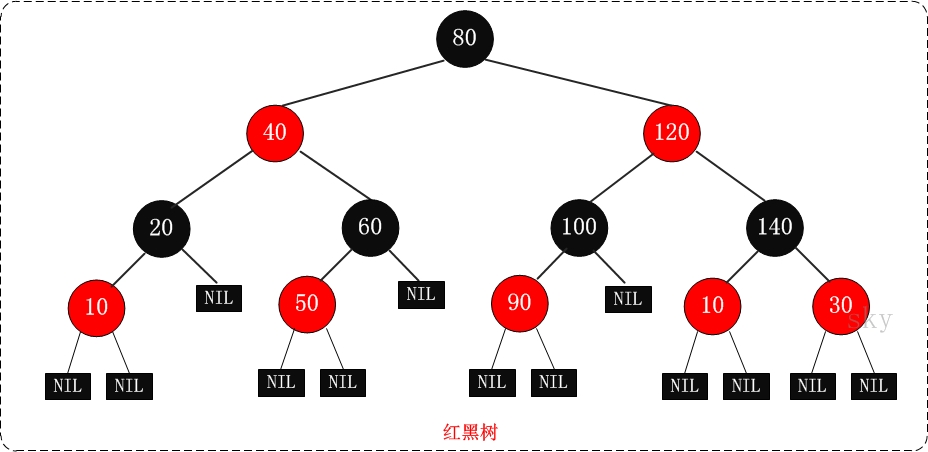
红黑树应用
java集合中TreeSet与TreeMap底层实现都采用的红黑数的思想,jdk1.8以后的hashmap底层(数组+链表)当链表元素超过8以后,自动转为红黑树
红黑树的基本操作
前言:首先定义红黑树的数据结构

1 class BRTree<T extends Comparable<T>>{//整棵树 2 private RBTNode<T> root; //根结点 3 4 private static final boolean RED = false; 5 private static final boolean BLACK = true; 6 7 public class RBTNode<T extends Comparable<T>> { //红黑树的节点类 8 boolean color; // 颜色 9 T key; // 关键字(键值) 10 RBTNode<T> left; // 左孩子 11 RBTNode<T> right; // 右孩子 12 RBTNode<T> parent; // 父结点 13 14 public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) { 15 this.key = key; 16 this.color = color; 17 this.parent = parent; 18 this.left = left; 19 this.right = right; 20 } 21 22 } 23 //...省略get和set方法 24 }
1.节点左旋
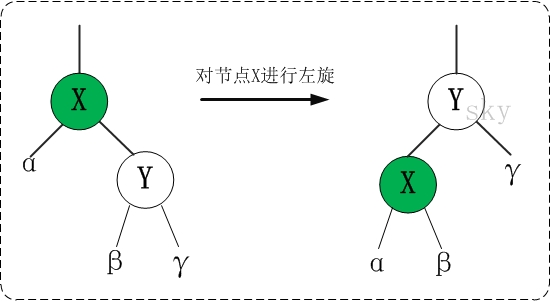
代码实现:

1 /* 2 * 对红黑树的节点(x)进行左旋转 3 * 4 * 左旋示意图(对节点x进行左旋): 5 * px px 6 * / / 7 * x y 8 * / \ --(左旋)-. / \ # 9 * lx y x ry 10 * / \ / \ 11 * ly ry lx ly 12 * 13 * 14 */ 15 private void leftRotate(RBTNode<T> x) { 16 // 设置x的右孩子为y 17 RBTNode<T> y = x.right; 18 19 // 将 “y的左孩子” 设为 “x的右孩子”; 20 // 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲” 21 x.right = y.left; 22 if (y.left != null) 23 y.left.parent = x; 24 25 // 将 “x的父亲” 设为 “y的父亲” 26 y.parent = x.parent; 27 28 if (x.parent == null) { 29 this.mRoot = y; // 如果 “x的父亲” 是空节点,则将y设为根节点 30 } else { 31 if (x.parent.left == x) 32 x.parent.left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 33 else 34 x.parent.right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 35 } 36 37 // 将 “x” 设为 “y的左孩子” 38 y.left = x; 39 // 将 “x的父节点” 设为 “y” 40 x.parent = y; 41 }
2.节点右旋
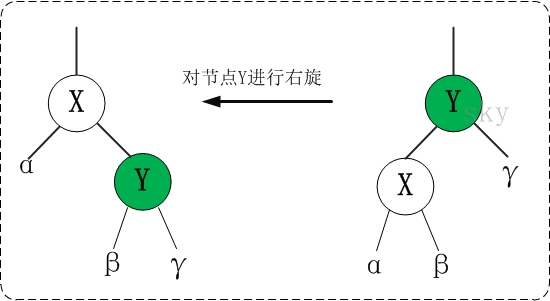

/* * 对红黑树的节点(y)进行右旋转 * * 右旋示意图(对节点y进行左旋): * py py * / / * y x * / \ --(右旋)-. / \ # * x ry lx y * / \ / \ # * lx rx rx ry * */ private void rightRotate(RBTNode<T> y) { // 设置x是当前节点的左孩子。 RBTNode<T> x = y.left; // 将 “x的右孩子” 设为 “y的左孩子”; // 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲” y.left = x.right; if (x.right != null) x.right.parent = y; // 将 “y的父亲” 设为 “x的父亲” x.parent = y.parent; if (y.parent == null) { this.mRoot = x; // 如果 “y的父亲” 是空节点,则将x设为根节点 } else { if (y == y.parent.right) y.parent.right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子” else y.parent.left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子” } // 将 “y” 设为 “x的右孩子” x.right = y; // 将 “y的父节点” 设为 “x” y.parent = x; }
3.添加节点
3.1 正常同二叉树插入节点(注:插入新节点时,将该节点颜色标记成红色,目的是标记成红色不会违背性质5,但是可能会违背性质4,所以需要重新修正红黑树)

public void insert(T key){ RBTNode<T> node = new RBTNode(key, BLACK, null, null, null); if(node != null){ insert(node); } } private void insert(RBTNode<T> node) { int cmp; RBTNode<T> y = null; RBTNode<T> x = this.mRoot; // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。 while (x != null) { y = x; cmp = node.key.compareTo(x.key); if (cmp < 0) x = x.left; else x = x.right; } node.parent = y; if (y!=null) { cmp = node.key.compareTo(y.key); if (cmp < 0) y.left = node; else y.right = node; } else { this.mRoot = node; } // 2. 设置节点的颜色为红色 node.color = RED; // 3. 将它重新修正为一颗二叉查找树 insertFixUp(node); }
3.2 重新修正红黑树

public void insertFixUp(RBTNode<T> node){ RBTNode<T> parent, gparent; while (((parent = node.parent)!=null) && !parent.color) { gparent = parent.parent; //若“父节点”是“祖父节点的左孩子” 即 gparent.left == parent if(gparent.left == parent){ //case1 : 祖父节点的右节点是红色 gparent.right.color = Red; RBTNode<T> uncle = gparent.right; if(uncle != null && !uncle.color){ uncle.color = BLACK; //将叔叔节点颜色置为黑色 parent.color = BLACK; //将父亲节点置为黑色 gparent.color = RED; //将祖父节点置为红色 node = gparent; //递归遍历 从下至上 continue; } //后续都是叔叔节点是黑色的 //case2 : 当前节点是右节点 if(parent.right == node){ RBTNode<T> temp; leftRotate(node); //左旋 temp = parent; parent = node; node = temp; } //case3 : 当前节点是左节点 parent.color = BLACK; gparent.color = RED; rightRotate(node); }else{//gparent.right == parent //case 4: 叔叔节点是红色 RBTNode<T> uncle = gparent.left; if(uncle != null && !uncle.color){ uncle.color = BLACK; //将叔叔节点颜色置为黑色 parent.color = BLACK; //将父亲节点置为黑色 gparent.color = RED; //将祖父节点置为红色 node = gparent; //递归遍历 从下至上 continue; } //case5 : 当前节点是左节点 if(parent.left == node){ RBTNode<T> temp; rightRotate(node); //左旋 temp = parent; parent = node; node = temp; } //case6 : 当前节点是右节点 parent.color = BLACK; gparent.color = RED; rightRotate(node); } } this.root.color = BLACK; }
4.删除节点(该部分代码完全没怎么看,也没有理解到删除的思路)
4.1 删除节点

public void insertFixUp(RBTNode<T> node){ RBTNode<T> parent, gparent; while (((parent = node.parent)!=null) && !parent.color) { gparent = parent.parent; //若“父节点”是“祖父节点的左孩子” 即 gparent.left == parent if(gparent.left == parent){ //case1 : 祖父节点的右节点是红色 gparent.right.color = Red; RBTNode<T> uncle = gparent.right; if(uncle != null && !uncle.color){ uncle.color = BLACK; //将叔叔节点颜色置为黑色 parent.color = BLACK; //将父亲节点置为黑色 gparent.color = RED; //将祖父节点置为红色 node = gparent; //递归遍历 从下至上 continue; } //后续都是叔叔节点是黑色的 //case2 : 当前节点是右节点 if(parent.right == node){ RBTNode<T> temp; leftRotate(node); //左旋 temp = parent; parent = node; node = temp; } //case3 : 当前节点是左节点 parent.color = BLACK; gparent.color = RED; rightRotate(node); }else{//gparent.right == parent //case 4: 叔叔节点是红色 RBTNode<T> uncle = gparent.left; if(uncle != null && !uncle.color){ uncle.color = BLACK; //将叔叔节点颜色置为黑色 parent.color = BLACK; //将父亲节点置为黑色 gparent.color = RED; //将祖父节点置为红色 node = gparent; //递归遍历 从下至上 continue; } //case5 : 当前节点是左节点 if(parent.left == node){ RBTNode<T> temp; rightRotate(node); //左旋 temp = parent; parent = node; node = temp; } //case6 : 当前节点是右节点 parent.color = BLACK; gparent.color = RED; rightRotate(node); } } this.root.color = BLACK; }
4.2 重新修正二叉树

private void removeFixUp(RBTNode<T> node,RBTNode<T> parent) { RBTNode<T> other; while ((node==null || node.color) && (node != this.root)) { if (parent.left == node) { other = parent.right; if (!other.color) { // Case 1: x的兄弟w是红色的 other.color = BLACK; parent.color =RED; leftRotate(parent); other = parent.right; } if ((other.left==null || other.left.color) && (other.right==null || other.right.color)) { // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 other.color = RED; node = parent; parent = node.parent; } else { if (other.right==null || other.right.color) { // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 other.left.color = BLACK; other.color = RED; rightRotate(other); other = parent.right; } // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 other.color = parent.color; parent.color = BLACK; other.right.color = BLACK; leftRotate(parent); node = this.root; break; } } else { other = parent.left; if (!other.color) { // Case 1: x的兄弟w是红色的 other.color = BLACK; parent.color = RED; rightRotate(parent); other = parent.left; } if ((other.left==null || other.left.color) && (other.right==null || other.right.color)) { // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 other.color = RED; node = parent; parent = node.parent; } else { if (other.left==null || other.left.color) { // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 other.right.color = BLACK; other.color = RED; leftRotate(other); other = parent.left; } // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 other.color = parent.color; parent.color = BLACK; other.left.color = BLACK; rightRotate(parent); node = this.root; break; } } } if (node!=null) node.color = BLACK; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号