快速傅里叶变换FFT学习笔记

点值表示法

我们正常表示一个多项式的方式，形如 $A(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n$，这是正常人容易看懂的，但是，我们还有一种表示法。

我们知道，$n+1$个点可以表示出一个 $n$ 次的多项式。

于是，我们任意地取 $n+1$ 个不同的值，表示 $x$ ，求出的值与 $x$ 对应，形成 $n+1$个点，这就可以表示。

复数

一种表示坐标的方法，对于坐标 $(x,y)$,可写作 $x+iy$，其中$x$为实部，$y$为虚部。

C++中有复数的模板，complex，可以直接作为变量类型使用。

运算规则，自然不用多说了，也就是直接拿式子算即可。

如果你不会，可以看看百度百科。

我们将点至原点的距离称为模长，将其与原点相连之后与 $x$ 轴形成的一个夹角称为辐角，不过呢，对于第三第四象限的点，自然要加上一个 $180°$了。

我的表述自然不够专业，希望可以表述出这个意思吧。

复数的乘法可以理解为，模长相乘，辐角相加。

Tips：

此部分的证明来自 cjx 犇犇。

为啥是这样呢？证明如下:

$$(a+bi)(c+di)=ac-bd+i(bc+ad)$$

那么这个点就是 $(ac-bd,bc+ad)$，其模长:

$$\begin{gathered} \sqrt{(ac-bd{)}^2+(bc+ad{)}^2} \\ =\sqrt{(ac{)}^2-2abcd+(bd{)}^2+(bc{)}^2+2abcd+(ad{)}^2} \\ =\sqrt{(ac{)}^2+(bd{)}^2+(bc{)}^2+(ad{)}^2} \\ =\sqrt{(a^2+b^2)(c^2+d^2)} \end{gathered}$$

那么我们应该可以看出来这个模长相乘了。

接下来是辐角相加，我们设原来两个辐角为 ${\theta }_1,{\theta }_2$，而模长为 $t_1,t_2$。

$$\begin{gathered} \cos ({\theta }_1+{\theta }_2)=\cos ({\theta }_1)\cos ({\theta }_2)-\sin ({\theta }_1)\sin ({\theta }_2) \\ =\frac{a}{t_1}\times \frac{c}{t_2}-\frac{b}{t_1}\times \frac{d}{t_2} \\ =\frac{ac-bd}{t_1{t}_2} \end{gathered}$$

我们知道分母是乘积的模长，分子是横坐标，所以这个式子恰好就是乘积辐角对应的 $\cos$ 值。

那么显然，辐角的值就是 ${\theta }_1+{\theta }_2$了。

把圆均分

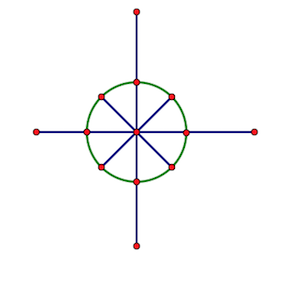
如图是坐标轴上一个以原点为圆心的半径为 $1$ 的圆。

我们定义${\omega }_n^k$表示从$(1,0)$开始，把圆均分为$n$份的第$k$个点的复数，其中$(1,0)$为${\omega }_n^0$。

那么，不难发现，${\omega }_n^k$表示的点为 $(\cos (2\pi \frac{k}{n}),\sin (2\pi \frac{n}{k}))$。

这是为什么呢？我们考虑它的辐角，由于其平分了一整个圆，所以其辐角为 $360\frac{k}{n}°$，转换为弧度后则为 $2\pi \frac{k}{n}$，且模长为 $1$，利用三角函数易得其坐标了。

简单推推式子不难发现 $({\omega }_n^1{)}^k={\omega }_n^k$，这是利用了模长相乘，辐角相加，因为模长是 $1$ ,怎么乘都是 $1$，于是辐角不断叠加，从定义上看是这样的。

• 性质1：${\omega }_{dn}^{dk}={\omega }_n^k$，根据定义可证。
• 性质2：${\omega }_n^{k+\frac{n}{2}}=-{\omega }_n^k$，两点对称。

这个东西有什么用呢？

离散傅里叶变换

离散傅里叶变换(Discrete Fourier Transform，简称DFT)的思想是利用 ${\omega }_n^k$将一个多项式转为点值表示法。

对于一个多项式$A(x)=a_0+a_{1}x+a_2{x}^2+...+a_{n-1}{x}^{n-1}$,我们按照前文所云，将所有的 ${\omega }_n^k$作为 $x$ 代入。

于是我们得到了 $n-1$ 个点，使用复数形式表示，成为一个数组 $(y_0,y_1,y_2,...,y_{n-1})$的。

这被称为 $A(x)$ 的傅里叶变换。

傅里叶逆变换

我们再将其作为一个多项式 $B(x)=y_0+y_{1}x+....+y_{n-1}{x}^{n-1}$。

对于这个多项式$B(x)$，代入所有的 ${\omega }_n^{-k}$，也就是${\omega }_n^k$的倒数，得到 $(z_0,z_1,z_2,...,z_{n-1})$。

易得：

$$\begin{gathered} z_k=\sum _{i=0}^{n-1}{y}_i({\omega }_n^{-k}{)}^i \\ =\sum _{i=0}^{n-1}(\sum _{j=0}^{n-1}{a}_j({\omega }_n^i{)}^j)({\omega }_n^{-k}{)}^i \\ =\sum _{j=0}^{n-1}{a}_j({\omega }_n^i{)}^j\sum _{i=0}^{n-1}({\omega }_n^{-k}{)}^i \\ =\sum _{j=0}^{n-1}{a}_j({\omega }_n^j{)}^i\sum _{i=0}^{n-1}({\omega }_n^{-k}{)}^i \\ =\sum _{j=0}^{n-1}{a}_j\sum _{i=0}^{n-1}({\omega }_n^{j-k}{)}^i \end{gathered}$$

关于后面那个等比数列，若 $j=k$，可得 $1$，否则用等比数列式子可知为 $0$。

因此：

$$\begin{gathered} z_k=n{a}_k \\ {a}_k=\frac{z_k}{n} \end{gathered}$$

所以我们可以求出原来的多项式了。

有几点需要注意：

• 我们提取 $a_i$ 只提取实部，因为虚部是虚数，无法经过我们的转换后变成实数。
• 数字有一定误差（毕竟你使用了三角函数等东西，小数是会有误差的），所以要四舍五入。

for(int i=0;i<=len-1;i++)
{
	ans[i]+=floor(a[i].real()/len+0.5);
}

快速傅里叶变换

快速傅里叶变换(Fast Fourier Transform，简称FFT)，是在 DFT的基础上我们发现时间复杂度依然需要 $O(n^2)$，没有含金量，所以我们要给他含金量！

我们可以使用分治的思想，使得时间复杂度降至$O(n\log n)$。

对于$A(x)=a_0+a_{1}x+a_2{x}^2+...+a_{n-1}{x}^{n-1}$，我们可以：

$$\begin{gathered} A_1(x)=a_0+a_{2}x+...,A_2(x)=a_1+a_{3}x+... \\ A(x)=A_1(x^2)+x{A}_2(x^2) \\ A({\omega }_n^k)=A_1({\omega }_n^{2k})+{\omega }_n^k{A}_2({\omega }_n^{2k}) \\ A({\omega }_n^k)=A_1({\omega }_{\frac{n}{2}}^k)+{\omega }_n^k{A}_2({\omega }_{\frac{n}{2}}^k) \end{gathered}$$

同理:

$$\begin{gathered} A({\omega }_n^{k+\frac{n}{2}})=A_1({\omega }_n^{2k+n})+{\omega }_n^{k+\frac{n}{2}}{A}_2({\omega }_n^{2k+n}) \\ A({\omega }_n^{k+\frac{n}{2}})=A_1({\omega }_{\frac{n}{2}}^k)-{\omega }_n^k{A}_2({\omega }_{\frac{n}{2}}^k) \end{gathered}$$

不错！利用这两个式子，我们可以在 $O(n\log n)$ 的时间复杂度求出 $A(x)$。

不过注意这里一直有一个除二操作，为了方便，我们需要把多项式补成一个次数为$2^x-1$ 的多项式。

可以写一个递归来求解。

注意这个取倒可以利用共轭复数，对于 $a+ib$，其共轭复数为 $a-ib$。

$$\frac{1}{a+ib}=\frac{a-ib}{(a+ib)(a-ib)}=\frac{a-ib}{a^2+b^2}$$

由于此处 $a^2+b^2=1$ ,因此其共轭复数为其倒数。

void FFT(cp *a,LL n,bool inv)//inv 表示omega是否取倒
{
	if(n==1)return;
	static cp buf[N];
	LL m=n/2;
	for(int i=0;i<=m-1;i++)buf[i]=a[2*i],buf[i+m]=a[2*i+1];//奇偶分开
	for(int i=0;i<=n-1;i++)a[i]=buf[i];
	FFT(a,m,inv),FFT(a+m,m,inv);
	for(int i=0;i<=m-1;i++)
	{
		cp x=omega(n,i);
		if(inv)x=conj(x);//conj(x)求解共轭复数
		buf[i]=a[i]+x*a[i+m],buf[i+m]=a[i]-x*a[i+m];
	}
	for(int i=0;i<=n-1;i++)a[i]=buf[i];
}

利用FFT求解多项式的乘积

这个还是十分简单的，直接把两个多项式转化为两个长度相同的次数为$2^x-1$的多项式。

求解出其傅里叶变换形式之后，对于每个点对应的复数，相乘即可。

为什么呢？

这里有一个误区大家要注意，$a_i$ 不是一个点，而是单纯因为 ${\omega }_n^i$是一个复数，所以 $a_i$ 才变成了一个复数，$a_i$只是表示$A({\omega }_n^i)$的值。

首先我们知道当前的 $a_i$表示的是 $A({\omega }_n^i)$，$b_i$表示的是 $B({\omega }_n^i)$，那么我们将两个值直接相乘。

因此多项式相乘以后，我们希望 $a_i=A({\omega }_n^i)B({\omega }_n^i)$，那么就是直接相乘喽。

给一个简单的实现：

#include<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{
    return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,x,len,ans[N];
cp a[N],b[N];
//上文的 FFT 实现省去
int main()
{
	scanf("%d",&n); 
	len=1;
	while(len<2*n)len*=2;
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);
	FFT(a,len,0),FFT(b,len,0);
	for(int i=0;i<=len-1;i++)a[i]*=b[i];
	FFT(a,len,1);
	for(int i=0;i<=len-1;i++)//进位
	{
		ans[i]+=floor(a[i].real()/len+0.5);
		ans[i+1]+=ans[i]/10;
		ans[i]%=10;
	}
	int i=len;
	for(i;i>=0&&ans[i]==0;i--);//前导零
	if(i==-1)len=0;
	for(;i>=0;i--)printf("%d",ans[i]); 
}

非递归FFT

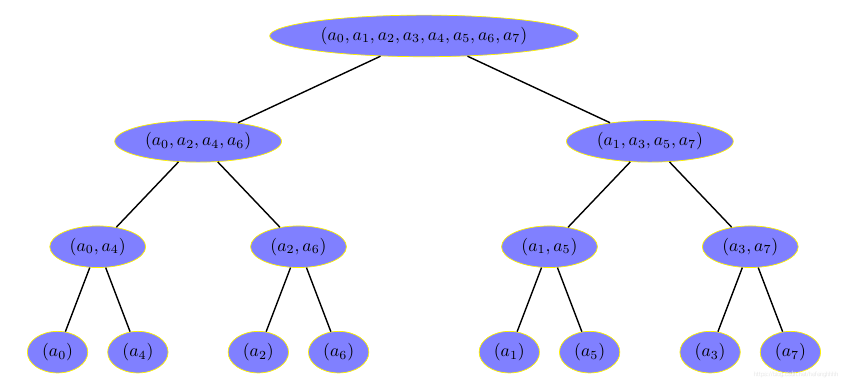
这里有一个优化，我们发现每次递归有一个把 $a_i$ 奇偶分开的过程，本质来看，就是将二进制末尾为 $0$ 的数字与二进制末尾为 $1$ 的数字分开。

我们不妨想一下，对于一个数 $x$，其位置可以根据其二进制确定，就是其二进制倒过来的数字。

我们先将每个 $a_i$ 放置在对应的位置，然后向上逐渐合并。

void FFT(cp *a,bool inv)
{
	LL lim=0;
	while((1<<lim)<len)lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)
			if((i>>j)&1)t|=(1<<(lim-j-1));//处理其翻转后的值
		if(i<t)swap(a[i],a[t]);
	}
	static cp buf[N];
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		for(LL j=0;j<=len-1;j+=l)
		{
			for(LL i=0;i<=m-1;i++)
			{
				cp x=omega(l,i+j);
				if(inv)x=conj(x);
				buf[i+j]=a[i+j]+x*a[i+j+m];
				buf[i+j+m]=a[i+j]-x*a[i+j+m];
			}
		}
		for(int j=0;j<=len-1;j++)a[j]=buf[j];
	}
}

蝴蝶操作

这个东西其实就是想了个办法使得把工具人数组 buf 除掉了。

调调顺序即可。

void FFT(cp *a,bool inv)
{
	LL lim=0;
	while((1<<lim)<len)lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)
			if((i>>j)&1)t|=(1<<(lim-j-1));
		if(i<t)swap(a[i],a[t]);
	}
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		for(LL j=0;j<=len-1;j+=l)
		{
			for(LL i=0;i<=m-1;i++)
			{
				cp x=omega(l,i+j);
				if(inv)x=conj(x);
				x*=a[i+j+m];
				a[i+j+m]=a[i+j]-x;
				a[i+j]=a[i+j]+x;
			}
		}
	}
}

一些小优化

对于 $i$ 的二进制翻转可以先预处理出来，我们用 $R_i$ 表示 $i$ 的二进制翻转。

然后 ${\omega }_n^k$ 可以利用性质累乘，会快很多，因为复数的各种操作常数巨大，直接累乘常数较小。

最后代码就长这样了：

#include<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{
    return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,len,lim,x,ans[N],r[N];
cp a[N],b[N];
void FFT(cp *a,bool inv)
{
	for(int i=0;i<=len-1;i++)
	{
		LL t=r[i];
		if(i<t)swap(a[i],a[t]);
	}
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		cp omg=omega(l,1);
		for(LL j=0;j<=len-1;j+=l)
		{
			cp x(1,0); 
			for(LL i=0;i<=m-1;i++)
			{
				cp t=x;
				if(inv)t=conj(t);
				t*=a[i+j+m];
				a[i+j+m]=a[i+j]-t,a[i+j]=a[i+j]+t;
				x*=omg;
			}
		}
	}
}
int main()
{
	scanf("%d",&n); 
	len=1;
	while(len<2*n)len*=2,lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1));
		r[i]=t;
	}
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);
	FFT(a,0),FFT(b,0);
	for(int i=0;i<=len-1;i++)a[i]*=b[i];
	FFT(a,1);
	for(int i=0;i<=len-1;i++)
	{
		ans[i]+=floor(a[i].real()/len+0.5);
		ans[i+1]+=ans[i]/10;
		ans[i]%=10;
	}
	int i=len;
	for(i;i>=0&&ans[i]==0;i--);
	if(i==-1)len=0;
	for(;i>=0;i--)printf("%d",ans[i]);
}

参考

胡小兔-小学生都能看懂的FFT！！！