堆排序(大顶堆/小顶堆)(C++)

1.什么是 堆

　　堆是一个用数组存放的一个完全二叉树，它可以被看成一个近似的完全二叉树，树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左向右填充。表示堆的数组A包括两个属性：A. length（通常）给出数组元素的个数，A. heap-size表示有多少个堆元素存储在该数组中。也就是说，虽然A[1.A. length]可能都存有数据，但只有A[1.A. heap-size]中存放的是堆的有效元素，这里，0≤A， heap-size≤A. length。树的根结点是A[1]，这样给定一个结点的下标i，根据完全二叉树的性质，我们很容易计算得到它的父结点、左子结点和右子结点的下标：i结点（i！=1）的父节点为i/2；左子节点为i*2，右子结点为i*2+1；

 

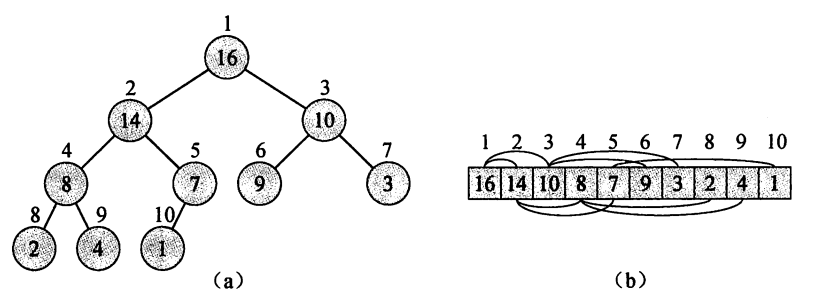
　　上图是以（a）二叉树和（b数组形式展现的一个最大堆。每个结点圆圈内部的数字是它所存储的数据。结点上方的数字是它在数组中相应的下标。数组上方和下方的连线显示的是父-子关系：父结点总是在它的孩子结点的左边。该树的高度为3，下标为4（值为8）的结点的高度为1。

 

 

2.堆排序的思想

   利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

    其基本思想为(大顶堆)：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

    操作过程如下：

     1)初始化堆：将R[1..n]构造为堆；

     2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

    因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

 大顶堆构造以及利用大顶堆对数据排序的代码如下：

 

#include <iostream>
#include <algorithm>

using namespace std;

void HeapAdjust(int *a,int i,int Size)//这里i表示第i个数，并不是数组下标，数组下标是从0开始的，第i个数在数组中为a[i-1];
{
    int r=2*i+1,l=2*i;//此时还是以序号标记
    int Max=i,mid;
    if(i<=Size/2){//确定当前i是否根结点
        //确定当前是否有右子结点，符合条件为有
        if(r<=Size){
            //有右结点的话判断谁大
            if(a[l-1]<a[r-1]) mid=r;
            else mid=l;
            // 将大的那个跟根结点比，如果子结点大则改变Max的指向
            if(a[mid-1]>a[i-1])  Max=mid;
        }
        //否则没有，没有的话判断是否有左子结点，有的话就与根结点对比
        else if(l<=Size && a[l-1]>a[i-1]) Max=l;
        //如果最大的节点不是根结点，则：
        if(Max!=i){
            swap(a[Max-1],a[i-1]);
            HeapAdjust(a,Max,Size);//这里主要是确定交换之后的子结点值依旧满足大根堆性质即大于子结点的子节点的值，可以将这条语句用递归理解，本质上是将较小的值沉到下面；
        }
    }
}

void BuildHeap(int *a,int Size)//建造二叉树堆
{
    int i;
    for(i=Size/2;i>=1;i--)//最大的无叶子结点是size/2；手画完全二叉树图即可以证明
        HeapAdjust(a,i,Size);
}

int main()
{
    int a[]={1,7,3,4,2,8,34,45,23,89,56,3,4,67};
    int Size=sizeof(a)/sizeof(a[0]);
    BuildHeap(a,Size);
        for(int i=0;i<Size;i++)//展示第一次建堆的结果
            cout<<a[i]<<' ';
    cout<<'\n';

    for(int i=Size;i>=1;i--){//逐个进行堆排序
        swap(a[0],a[i-1]);
        HeapAdjust(a,1,i-1);
    }

    for(int i=0;i<Size;i++)//展示最终排序结果
        cout<<a[i]<<' ';
    cout<<'\n';
    return (0);
}
    

 

 

 

  小顶堆构造以及利用小顶堆对数据排序的代码如下：

#include <iostream>
#include <algorithm>

using namespace std;

void HeapAdjust(int *a,int i,int Size)//这里i表示第i个数，并不是数组下标，数组下标是从0开始的，第i个数在数组中为a[i-1];
{
    int r=2*i+1,l=2*i;//此时还是以序号标记
    int Min=i,mid;
    if(i<=Size/2){//确定当前i是否根结点
        //确定当前是否有右子结点，符合条件为有
        if(r<=Size){
            //有右结点的话判断谁小
            if(a[l-1]>a[r-1]) mid=r;
            else mid=l;
            // 将大的那个跟根结点比，如果子结点小则改变Min的指向
            if(a[mid-1]<a[i-1])  Min=mid;
        }
        //否则没有，没有的话判断是否有左子结点，有的话就与根结点对比
        else if(l<=Size && a[l-1]<a[i-1]) Min=l;
        //如果最大的结点不是根结点，则：
        if(Min!=i){
            swap(a[Min-1],a[i-1]);
            HeapAdjust(a,Min,Size);//这里主要是确定交换之后的子结点值依旧满足小根堆性质即小于子结点的子结点的值，可以将这条语句用递归理解，本质上是将较大的值沉到下面；
        }
    }
}

void BuildHeap(int *a,int Size)//建造二叉树堆
{
    int i;
    for(i=Size/2;i>=1;i--)//最大的无叶子结点是size/2；手画完全二叉树图即可以证明
        HeapAdjust(a,i,Size);
}

int main()
{
    int a[]={1,7,3,4,2,8,34,45,23,89,56,3,4,67};
    int Size=sizeof(a)/sizeof(a[0]);
    BuildHeap(a,Size);
        for(int i=0;i<Size;i++)//展示第一次建堆的结果
        cout<<a[i]<<' ';
    cout<<'\n';

    for(int i=Size;i>=1;i--){//逐个进行堆排序
        swap(a[0],a[i-1]);
        HeapAdjust(a,1,i-1);
    }

    for(int i=0;i<Size;i++)//展示最终排序结果
        cout<<a[i]<<' ';
    cout<<'\n';
    return (0);
}

 

参考文献：

【1】Matrix海子，"堆排序"，https://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html.

【2】（美）ThomasH.Cormen，CharlesE.Leiserson，RonaldL.Rivest，CliffordStein著；王刚，邹恒明，殷建平，王宏志等译. 算法导论 原书第3版. 北京：机械工业出版社, 2013.01.