西瓜书读书笔记
1.绪论
1.1 引言
机器学习所研究的主要内容,是关于在计算机上从数据中产生"模 型" (model) 的算法,即"学习算法" (learning algorithm)
1.2基本术语
数据集:这组记录的集合。
样本sample(示例instance): 数据集合中的每条记录或者对象的描述。
属性" (attribute) 或"特征 (feature): 反映事件或对象在某方面的表现或性质的事项。
属性值:属性上的取值
属性空间(attribute space)、 "样本空间" (samp1e space)或"输入空间: 属性张成的空间
特征向量:由于空间中的每个点对应一个坐标向量
标记空间/输出空间:(xi, yi) 表示第i个样例, 其中执 yi∈Y 是示例 Xi 的标记, Y 是所有标记的集合。
分类:预测值是离散值,例如 好瓜,坏瓜
二分类:通常称其中一个类为 "Æ类" (positive class 另一个类为"反类" (negative class)
多分类:涉及多个类别时
1.3 假设空间
归纳学习 (inductive learning:归纳(induction)与横绎(deductio)是科学推理的两大基本手段.前者是从 特殊到一般的"泛化" (generalization)过程,即从具体的事实归结出一般性规 律;后者则是从一般到特殊的"特化" (specializatio叫过程,即从基础原理推演 出具体状况.例如,在数学公理系镜中,基于一组公理和推理规则推导出与之 相洽的定理,这是演绎;而"从样例中学习"显然是一个归纳的过程。
概念学习:广义的归纳学习大体相当于从样例中学习, 而狭义的归纳学习则要求从训练数据中学得概念(concept)
假设空间:监督学习的目的在于学习一个由输入到输出的映射,这一映射由模型来表示。换句话说,学习的目的就在于找到最好的这样的模型。模型属于由输入空间到输出空间的映射集合,这个集合就是假设空间(hypothesis space)。假设空间的确定意味着学习范围的确定。
1.4归纳偏好
归纳偏好:机器学习算法在学习过程中对某种类型假设的偏好
奥卡姆剃刀:若有多个假设和观察一致,选择最简单的那个。(但有时奥卡姆剃刀也会有不适用,当无法判断哪个更简单时,需要其他机制来解决这个问题)
2 模型评估与选择
2.1 经验误差与过拟合
错误率(Error Rate):分类错误的样本数 / 样本总数
精度(Accuracy):1 - 错误率
误差(Error):学习器实际预测输出和样本真实输出之间的差异
训练误差(Training Error)/经验误差(Empirical Error):学习器在训练集上的误差
泛化误差(Generalization Error):学习器在新样本上的误差
过拟合(Overfitting):学习器将训练样本学的太好,导致泛化性能下降。过拟合无法避免只能缓解
欠拟合(Underfitting):学习器学习能力低下造成
2.2评估方法
2.2.1 留出法
留出法: 直接将数据集划分为两个互斥的集合,一个为训练集一个为测试集。且训练/测试集的划分要尽可能保持数据分布的一致性,避免 困数据划分过程引入额外的偏差而对最终结果产生影响,单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作 为留出法的评估结果.
2.2.2 交叉验证法
交叉验证法:先将数据集 D 划分为 k 个大小相似的 互斥子集,例如下图
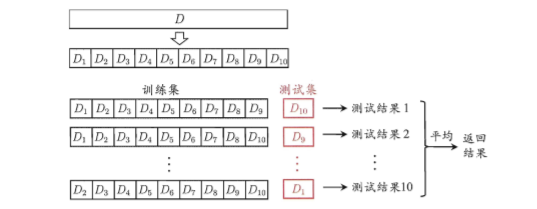
将数据划分为K份,保证每份数据不重叠,全部数据不遗漏。分类任务中,划分过程尽量保证每份预测的类别比例相同。
特例当k = m时候得留一法
留一法不受随机样本的影响,评估结果一般来说较为准确。但是数据量较大时候会计算会消耗很大
2.2.3 自助法
自助法:就是将样本分为两块D为整体样本D1为空样本
将D中的样本随机抽取到D1中抽取n次,然后将D1作为训练集D作为测试集,虽然有重复,但是通过计算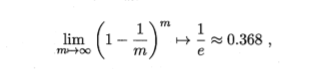
还是有36%没有出现在样本中,所以可以将D作为测试集,自助法只适合大量数据的情况,因为小量数据没发划分训练集和测试集
2.3 性能度量
错误率(error rate):分类错误的样本数占样本总数的比例;
精度(accuracy):分类正确的样本数占样本总数的比例;
查准率、查全率与F1:
对于二分类问题,根据真实类别与机器学习预测结果:真正例(true positive)、假正例(false positive)、真反例(true negative)和 假反例(false negative)。

查准率:是基于「预测数据」,考察「真正例」的占比。
查全率:是基于「真实数据」,考察「真正例」的占比。
查准率和查全率是一对矛盾的度量,查准率越高查全率越低,反之亦然!
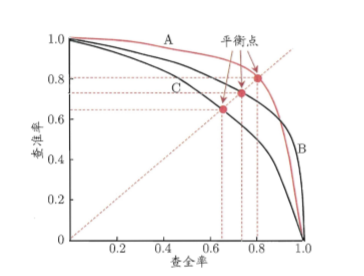
若一个学习器的曲线被另一个学习器的曲线完全 包住 则后者性能优于前者(A >C)。可以理解为对于C中任意一点,A中总可以至少找到一个比此点对应的查准率值和查全率值都要大。
若两个曲线有交叉则无法确定,只能在具体的查准率或查全率条件下进行比较,后为了方便比较设计了平衡点 (Break-Event Point,简称 BEP),查准率=查全率
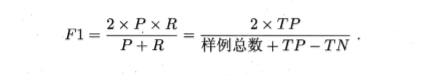

2.4 比较检验
比较检验:在比较学习器泛化性能的过程中,统计假设检验(hypothesis test)为学习器性能比较提供了重要依据,即若A在某测试集上的性能优于B,那A学习器比B好的把握有多大。
假设检验:关于单个学习器泛化性能的假设进行检验;假设测试错误率为a,通过统计学公式计算可得,在A概率下泛化错误率小于等于a,在1-A概率下泛化错误率大于a。概率A反映了结论的“置信度”(confidence)
交叉验证t检验:

相比于假设检验是得到单个学习器的泛化错误率的大致范围假设,交叉检验方法就是在比较A、B两学习器性能的优劣。
McNemar 检验:
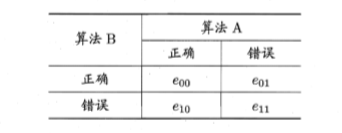
若我们做的假设是两学习器性能相同?则应有 e01= e10,那么变量 |e01 - e10| 应当服从正态分布,且均值为 1,方差为 e01 十 e10.回此变量服从自由度为 1 的 χ2 分布,即标准正态分布变量的平方.给定显著度 α,当以 上变量恒小于临界值功时,不能拒绝假设,即认为两学习器的性能没有显著差 别;否则拒绝假设,即认为两者性能有显著差别
Friedman 检验与 Nenenyl 后续检验:
原始Friedman 检验:
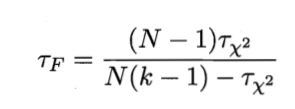
TF 服从自由度为 k-1 和 (k-1)(N-1)的F分布。
Nemenyi后续检验:当假设“所有算法的性能相同”被拒绝的时候,需采用后续检验来进一步区分各算法,该算法计算出平均序值差别的临界值域,若两个算法的平均序值之差超过临界值域,则应以相应的置信度拒绝“两个算法性能相同”这一假设。
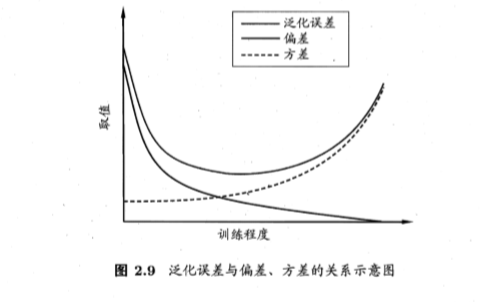
2.5 偏差与方差
方差:使用样本数相同的不同训练集产生的方差。
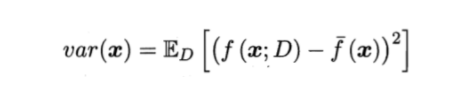
偏差:期望输出与真实标记的差别。
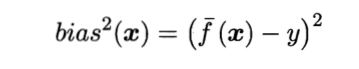
噪声:数据集标记和真实标记的方差。
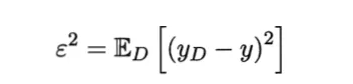
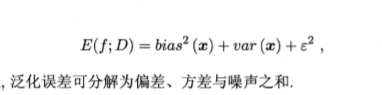


 浙公网安备 33010602011771号
浙公网安备 33010602011771号