筛素数的方法

朴素筛法（埃氏筛法）

思路：将当前数i的所有倍数（一定是合数）筛掉。

如：当i=2时，将4,6,8,10...筛掉，当i=3时将6,9,12...筛掉。

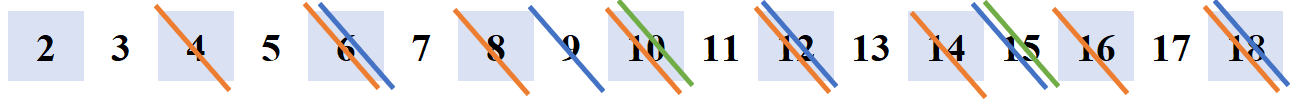
很明显这种筛法有很多元素被重复筛了，如筛6时，i=2时筛了一遍，i=3时又筛了一遍。

代码：

int prime[N], cnt;
bool st[N];

void isPrime(int n){
    for(int i = 2; i <= n; i ++ ){
        if(!st[i]){
            prime[cnt ++ ] = i;
            for(int j = 2 * i; j <= n; j += i){
                st[j] = true;
            }
        }
    }
}

线性筛法

该种方法完美解决了上面晒法有些元素会被重复筛多次的缺陷。

思路：筛掉当前数i的某些质因数倍的数：从小到大枚举所有质数，若当前质数能被i整除，立即跳出循环。
这种方式被筛掉的数，都是被它的最小质因数乘上某个数筛掉的，比如15的最小质因数是3.
如：i=2，筛掉4；
i=3，筛掉6,9；
i=4，筛掉8；
i=5，筛掉10,15,25；
i=6，筛掉12；

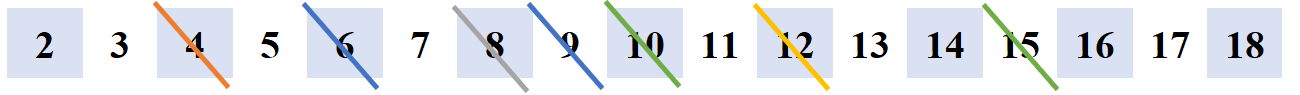
从上图也可看出，每个合数只被划掉了一次。

原因如下：当i=6时，只筛到了12就结束了，并没有筛掉18，因为18=2 * 3 * 3；也就是说，i=9时，也可以把18筛掉。
18的最小质因数是2，因为每次循环prime[j]都是从2开始，也就是说，18必然会被2*9筛掉。

代码：

int prime[N], cnt;
bool st[N];

void isPrime(int n){
    for(int i = 2; i <= n; i ++ ){
        if(!st[i]) prime[cnt ++ ] = i;
        for(int j = 0; prime[j] <= n / i; j ++ ){
            st[prime[j] * i] = true;
            if(i % prime[j] == 0) break;
        }
    }
}