分类模型校准：ROC-AUC不够？用ECE/pMAD评估概率质量

如果一个项目的核心不是分类准确率，而是概率估计的质量。换句话说，需要的是一个校准良好的模型。这里校准的定义是：如果模型给一批样本都预测了25%的正例概率，那这批样本中实际的正例比例应该接近25%。这就是校准。

解决这个校准问题单看ROC-AUC不够，要用Brier score或者Log-loss来保证校准质量。

我们先介绍一下我们一般使用的的几个指标：

ROC-AUC衡量的是模型区分正负样本的排序能力，跟预测概率的绝对值无关。

Brier score本质上就是预测概率的均方误差：

1. brier_score=np.mean((y_proba-y_true) **2)

Log-loss则是从似然的角度评估概率质量：

1. log_loss=-np.mean(y_true*np.log(y_proba) + (1-y_true) *np.log(1-y_proba))

这里用PyCaret的Bank数据集做演示：随机抽取100组不同的特征子集，每组特征分别训练4种模型（Logistic Regression、Decision Tree、Random Forest、LightGBM），得到400个候选模型。所有指标都在独立的测试集上计算。

校准图的可视化逻辑

评估校准最直观的方式是画校准图。方法是把预测概率分成若干区间，每个区间内比较平均预测概率（x轴）和实际正例比例（y轴）。

随机挑一个模型，看看它的校准图长什么样。下面同时画出预测概率的分布直方图。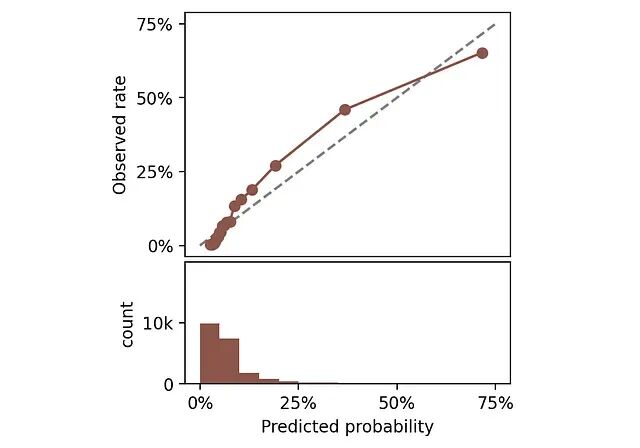

顶部：校准图。底部：预测概率直方图。

完美校准的模型，曲线应该贴着45度对角线。比如某个区间平均预测概率是25%，那这个区间里实际正例比例也该是25%。曲线偏离对角线越远说明校准越差。

https://avoid.overfit.cn/post/5a1fb11ae77b480cb2b5a814684e3330