MARS算法理论和Python代码实现:用分段回归解决非线性时间序列预测问题
多元自适应回归样条(Multivariate Adaptive Regression Splines, MARS)是Jerome Friedman于1991年提出的一种非参数回归技术。该方法专门用于建模预测变量集合与目标变量之间的复杂非线性关系,无需预先确定具体的函数形式。本文将深入探讨MARS算法的核心原理,并详细阐述其在时间序列预测任务中的应用策略与技术实现。
线性回归模型的局限性分析
在理解MARS算法的优势之前,有必要首先分析传统线性模型所面临的技术挑战。当提及"线性模型"时,通常指的是线性回归方法。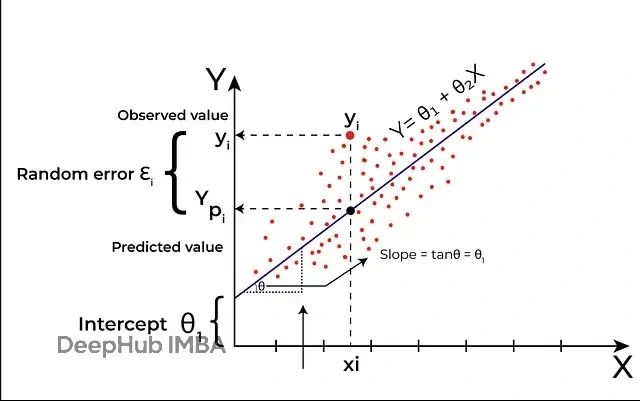
线性回归模型存在三个根本性的技术限制。首先,该模型严格假设变量间存在线性关系,因此无法有效捕获数据中的曲线特征、阈值效应或斜率突变现象。其次,线性回归对多重共线性问题极为敏感,当预测变量之间存在高度相关性时,会导致回归系数估计的不稳定性和可靠性下降。第三,该方法在处理复杂特征交互时存在明显不足,需要研究者预先明确指定交互项,这在缺乏先验知识的情况下往往难以实现。
现实世界中的大多数问题都涉及非线性关系,这使得传统线性回归的应用受到显著限制。
https://avoid.overfit.cn/post/ccdfceaeddde410db16ccc3d035ec4de


 浙公网安备 33010602011771号
浙公网安备 33010602011771号