高效处理多维数组：einsum()函数从入门到精通

爱因斯坦求和约定基础

我们从一个经典案例入手：矩阵乘法。在线性代数中，两个矩阵A和B相乘的标准定义是计算A中每一行与B中每一列的点积。图形化表示如下：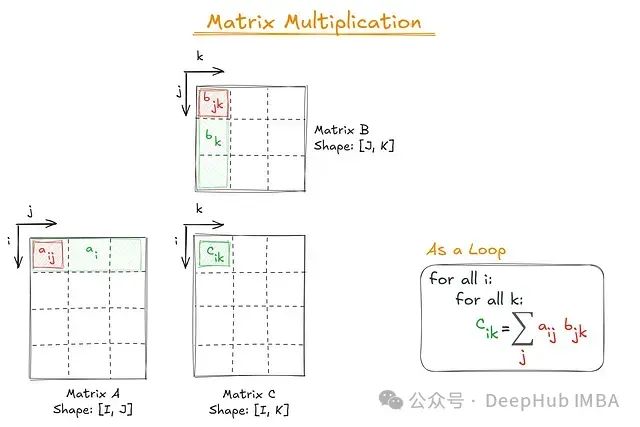

图1：标准矩阵乘法示意图。

注意观察，对于结果矩阵C中的每个元素，我们取A的第i行和B的第k列对应位置的元素相乘，然后对索引j求和。

这种元素级乘法和求和模式在张量运算中极为常见，尤其在阿尔伯特·爱因斯坦的广义相对论研究中。爱因斯坦为简化复杂张量表达式，提出了一种简洁表示法，省略显式的求和符号。其核心原则是：当一个索引在表达式中出现两次，则默认对该索引进行求和。

因此，对于矩阵乘法，我们可以表示为：

图2：使用爱因斯坦表示法的矩阵乘法。

 

https://avoid.overfit.cn/post/2c4838dc17614a43b57ac27b21747c37