PINN应用案例：神经网络求解热扩散方程高质量近似解

偏微分方程(PDE)是描述物理现象的基础数学工具。在简化几何形状的理想条件下，某些PDE问题可获得精确解析解。然而对于具有复杂边界和多维几何特征的实际工程问题，解析解通常难以获取或根本不存在。

传统求解PDE的主流方法是有限元法(FEM)。该方法将计算域离散化为网格单元，通过计算各单元间的相互作用来估算局部区域内的PDE残差。求解过程从初始近似解开始，通过迭代优化不断调整节点状态参数（如位置、应力、温度等物理量），直至系统收敛到稳定配置。

尽管有限元法在工程领域取得了巨大成功，但其高度依赖于网格质量和离散化精度，在处理复杂几何形状、多尺度问题或高维空间时面临计算效率和精度挑战。这些局限性促使研究人员积极探索新型求解策略，物理信息神经网络(PINN)作为一种新兴方法应运而生。

物理信息神经网络(Physics-informed Neural Networks, PINN)框架旨在构建满足初始条件和边界条件的偏微分方程近似解。该方法的核心优势在于PDE中的偏导数项可通过自动微分技术精确计算，这源于神经网络输出对其可调参数和输入变量天然具备可微特性。

PINN框架的关键组成是一个特殊设计的损失函数，其中包含微分方程残差项。该残差项量化了神经网络解与PDE描述的物理定律之间的偏离程度。损失函数还整合了衡量初始条件和边界条件满足程度的额外项。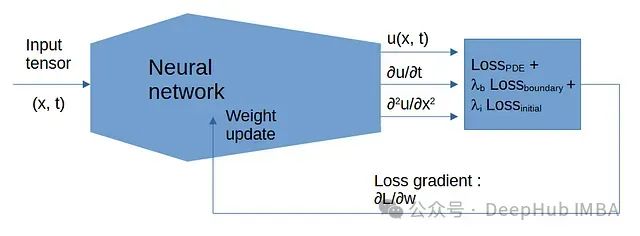

 

https://avoid.overfit.cn/post/26354859615b43f2af35addc1d0aee81