PyTorch PINN实战：用深度学习求解微分方程

神经网络技术已在计算机视觉与自然语言处理等多个领域实现了突破性进展。然而在微分方程求解领域，传统神经网络因其依赖大规模标记数据集的特性而表现出明显局限性。物理信息神经网络(Physics-Informed Neural Networks, PINN)通过将物理定律直接整合到学习过程中，有效弥补了这一不足，使其成为求解常微分方程(ODE)和偏微分方程(PDE)的高效工具。

传统神经网络模型需要依赖规模庞大的标记数据集，而这类数据的采集往往成本高昂且耗时显著。PINN通过将物理定律（具体表现为微分方程）融入训练过程，显著提高了数据利用效率。这种方法使得在流体动力学、量子力学和气候系统建模等科学领域实现基于数据的科学发现成为可能，为跨学科研究提供了新的技术路径。

神经网络基础理论

在深入剖析PINN之前，有必要回顾标准神经网络的核心运作机制：

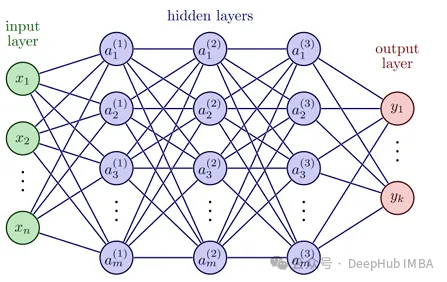
神经网络的基本计算单元是神经元，它接收加权输入信号，经过激活函数处理后产生输出值。多层神经元通过特定拓扑结构组织形成深度神经网络(DNN)，这种结构使网络能够逼近高度复杂的非线性函数。网络训练过程中，通常采用均方误差(MSE)等损失函数量化预测值与真实值之间的偏差。通过反向传播算法和梯度下降优化方法，网络权重参数被迭代调整以使损失函数最小化。

示例损失函数

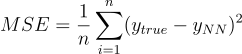
均方误差

PINN的技术特性与创新点

PINN与传统神经网络的根本区别在于，它不依赖于标记数据集进行学习，而是将微分方程约束直接嵌入到损失函数中。这意味着模型学习得到的函数_yNN(x)_需同时满足：

• 给定的微分方程约束条件
• 特定的边界条件和初始条件

 

https://avoid.overfit.cn/post/f9bd046772f1473a80002f592e9527d4