基于趋势和季节性的时间序列预测

时间序列预测是基于时间数据进行预测的任务。它包括建立模型来进行观测，并在诸如天气、工程、经济、金融或商业预测等应用中推动未来的决策。

本文主要介绍时间序列预测并描述任何时间序列的两种主要模式(趋势和季节性)。并基于这些模式对时间序列进行分解。最后使用一个被称为Holt-Winters季节方法的预测模型，来预测有趋势和/或季节成分的时间序列数据。

为了涵盖所有这些内容，我们将使用一个时间序列数据集，包括1981年至1991年期间墨尔本(澳大利亚)的温度。这个数据集可以从这个Kaggle下载，也可以本文最后的GitHub下载，其中包含本文的数据和代码。该数据集由澳大利亚政府气象局托管，并根据该局的“默认使用条款”(Open Access Licence)获得许可。

导入库和数据

首先，导入运行代码所需的下列库。除了最典型的库之外，该代码还基于statsmomodels库提供的函数，该库提供了用于估计许多不同统计模型的类和函数，如统计测试和预测模型。

1. from datetime import datetime, timedelta
2. import matplotlib.pyplot as plt
3. import numpy as np
4. import pandas as pd
5. import statsmodels.api as sm
6. from statsmodels.tsa.stattools import adfuller, kpss
7. from statsmodels.tsa.api import ExponentialSmoothing
8. %matplotlib inline

下面是导入数据的代码。数据由两列组成，一列是日期，另一列是1981年至1991年间墨尔本(澳大利亚)的温度。

1. # date
2. numdays = 365*10 + 2
3. base = '2010-01-01'
4. base = datetime.strptime(base, '%Y-%m-%d')
5. date_list = [base + timedelta(days=x) for x in range(numdays)]
6. date_list = np.array(date_list)
7. print(len(date_list), date_list[0], date_list[-1])
9. # temp
10. x = np.linspace(-np.pi, np.pi, 365)
11. temp_year = (np.sin(x) + 1.0) * 15
12. x = np.linspace(-np.pi, np.pi, 366)
13. temp_leap_year = (np.sin(x) + 1.0)
14. temp_s = []
15. for i in range(2010, 2020):
16. if i == 2010:
17. temp_s = temp_year + np.random.rand(365) * 20
18. elif i in [2012, 2016]:
19. temp_s = np.concatenate((temp_s, temp_leap_year * 15 + np.random.rand(366) * 20 + i % 2010))
20. else:
21. temp_s = np.concatenate((temp_s, temp_year + np.random.rand(365) * 20 + i % 2010))
22. print(len(temp_s))
24. # df
25. data = np.concatenate((date_list.reshape(-1, 1), temp_s.reshape(-1, 1)), axis=1)
26. df_orig = pd.DataFrame(data, columns=['date', 'temp'])
27. df_orig['date'] = pd.to_datetime(df_orig['date'], format='%Y-%m-%d')
28. df = df_orig.set_index('date')
29. df.sort_index(inplace=True)
30. df

可视化数据集

在我们开始分析时间序列的模式之前，让我们将每个垂直虚线对应于一年开始的数据可视化。

1. ax = df_orig.plot(x='date', y='temp', figsize=(12,6))
2. xcoords = ['2010-01-01', '2011-01-01', '2012-01-01', '2013-01-01', '2014-01-01',
3. '2015-01-01', '2016-01-01', '2017-01-01', '2018-01-01', '2019-01-01']
4. for xc in xcoords:
5. plt.axvline(x=xc, color='black', linestyle='--')
6. ax.set_ylabel('temperature')

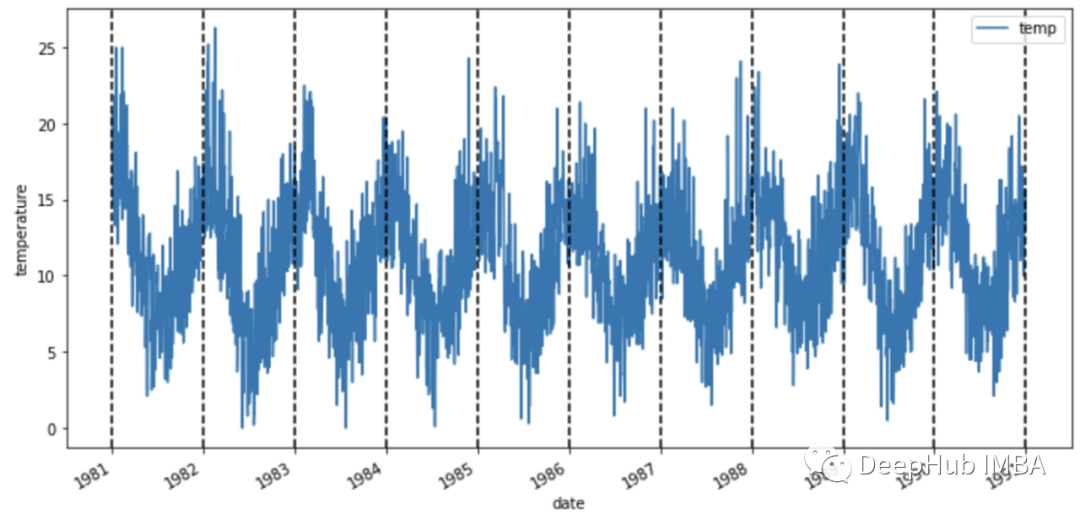
在进入下一节之前，让我们花点时间看一下数据。这些数据似乎有一个季节性的变化，冬季温度上升，夏季温度下降(南半球)。而且气温似乎不会随着时间的推移而增加，因为无论哪一年的平均气温都是相同的。

时间序列模式

时间序列预测模型使用数学方程(s)在一系列历史数据中找到模式。然后使用这些方程将数据[中的历史时间模式投射到未来。

有四种类型的时间序列模式:

趋势:数据的长期增减。趋势可以是任何函数，如线性或指数，并可以随时间改变方向。

季节性:以固定的频率(一天中的小时、星期、月、年等)在系列中重复的周期。季节模式存在一个固定的已知周期

周期性:当数据涨跌时发生，但没有固定的频率和持续时间，例如由经济状况引起。

噪音:系列中的随机变化。

完整文章

https://avoid.overfit.cn/post/51c2316b0237445fbb3dbf6228ea3a52