树与二叉树:数据结构基础解析

树的基本概念
树是⼀种非线性的数据结构,它是由n(n>=0)个有限结点组成⼀个具有层次关系的集合。把它叫做
树是因为它看起来像⼀棵倒挂的树,也就是说它是根朝上,⽽叶朝下的。它具有以下的特点:
• 有⼀个特殊的结点,称为根结点,根结点没有前驱结点
• 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每⼀个集合Ti(1 <= i <= m) ⼜是⼀棵与树类似的⼦树。每棵⼦树的根结点有且只有⼀个前驱,可以有0个或多个后
继
• 树是递归定义的。
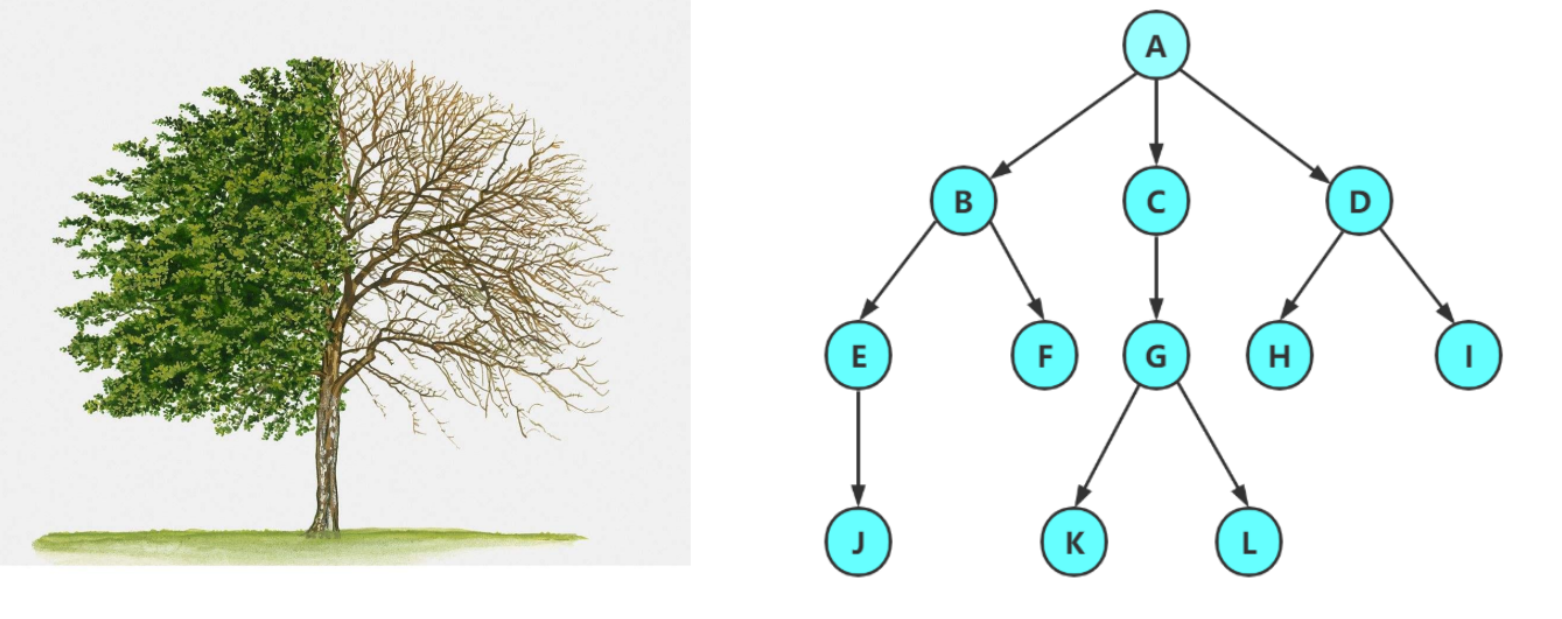
- 注意:树形结构中,⼦树之间不能有交集,否则就不是树形结构
![在这里插入图片描述]()
常用定义概念
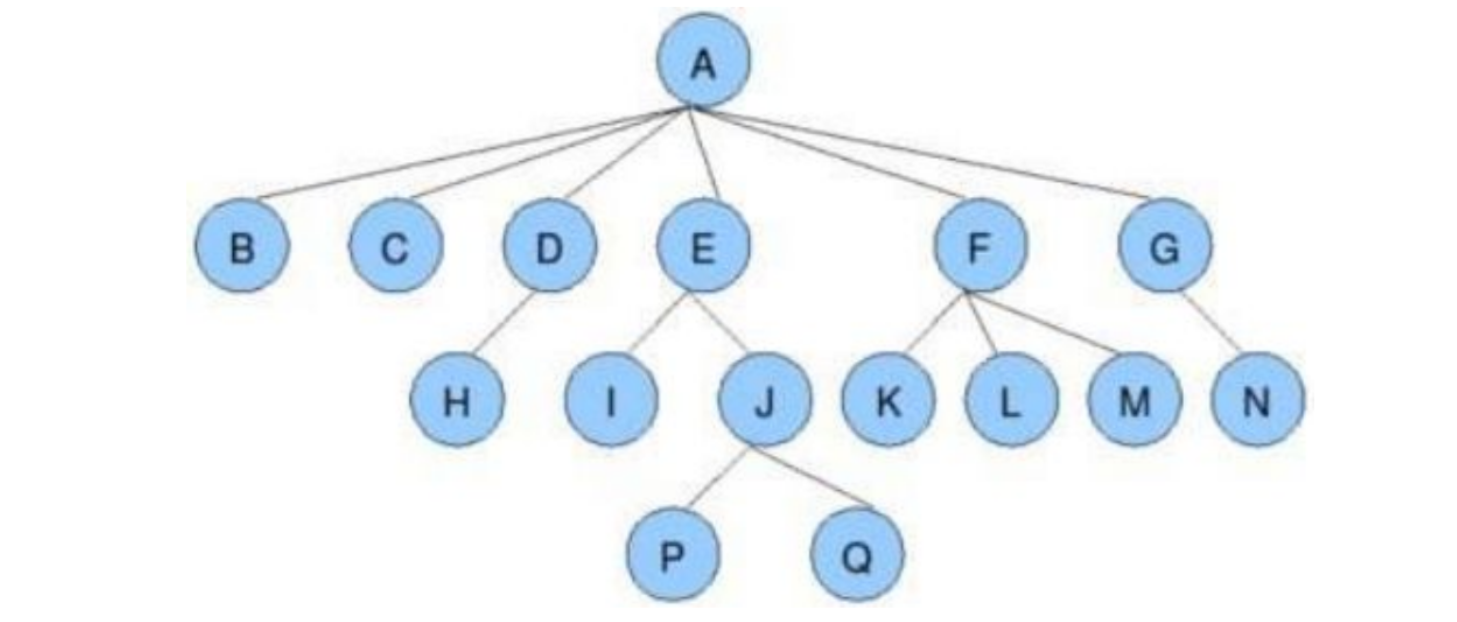
- 结点的度:一个结点含有子树的个数称为该结点的度;如上图:A的度为6
- 树的度:一棵树中,所有结点度的最大值称为树的度;如上图:树的度为6
- 叶子结点或终端结点:度为0的结点称为叶结点;如上图:B、C、H、I…等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;如上图:B是A的孩子结点
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次;如上图:树的高度为4
- 树的以下概念只需了解,在看书时只要知道是什么意思即可:
- 非终端结点或分支结点:度不为0的结点;如上图:D、E、F、G…等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点;如上图:B、C是兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
二叉树
概念
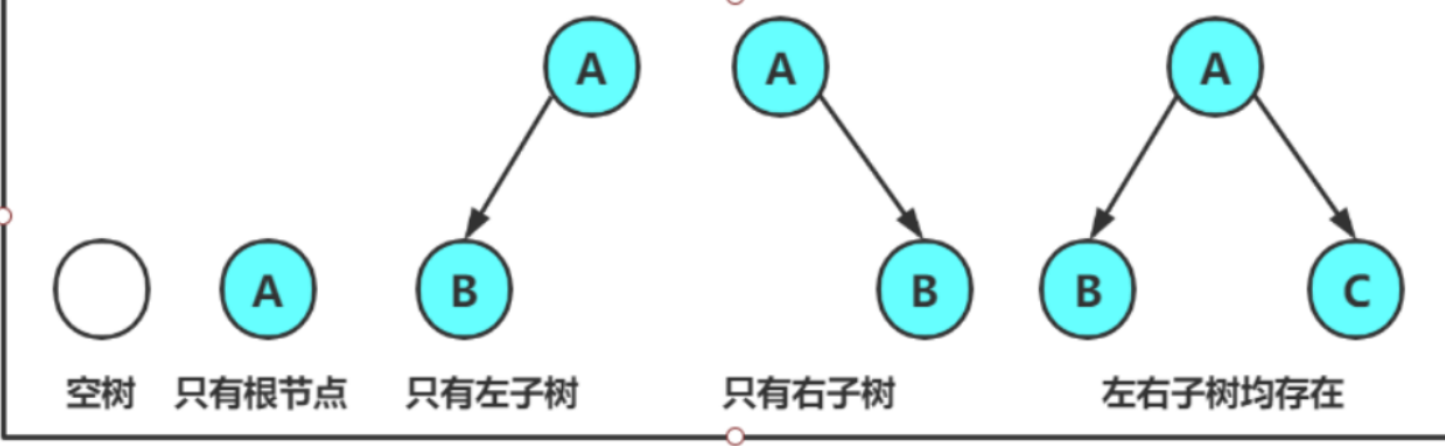
- 一颗二叉树是结点的一个有限集合,该集合:
- 或者为空
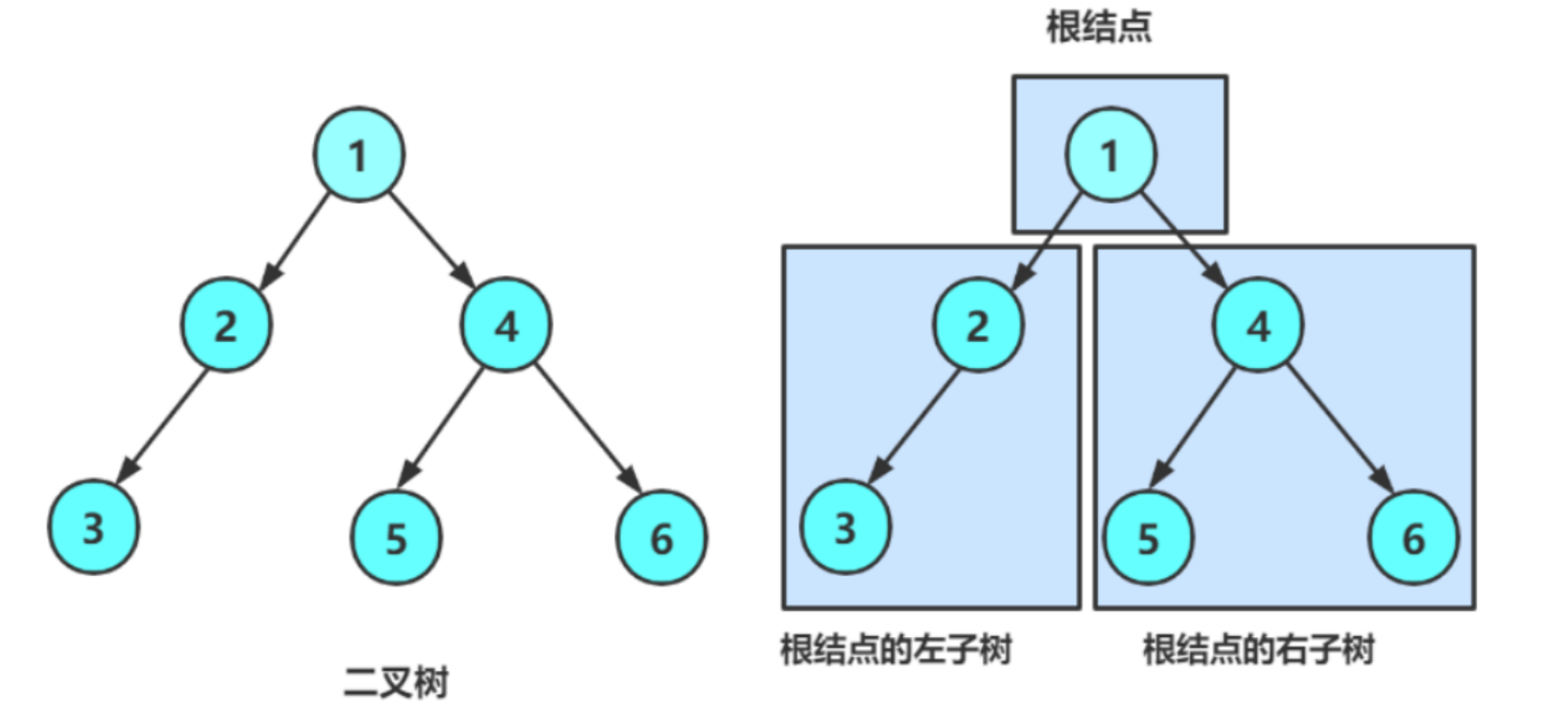
- 或者是由⼀个根节点加上两棵别称为左子树和右子树的二叉树组成
![在这里插入图片描述]()
- 注意点:
- 二叉树节点最多能延伸出两个节点
- 二叉树的左右节点有顺序之分,不能交换(后面前中后遍历顺序输出就不一样)
![在这里插入图片描述]()
两种特殊的二叉树
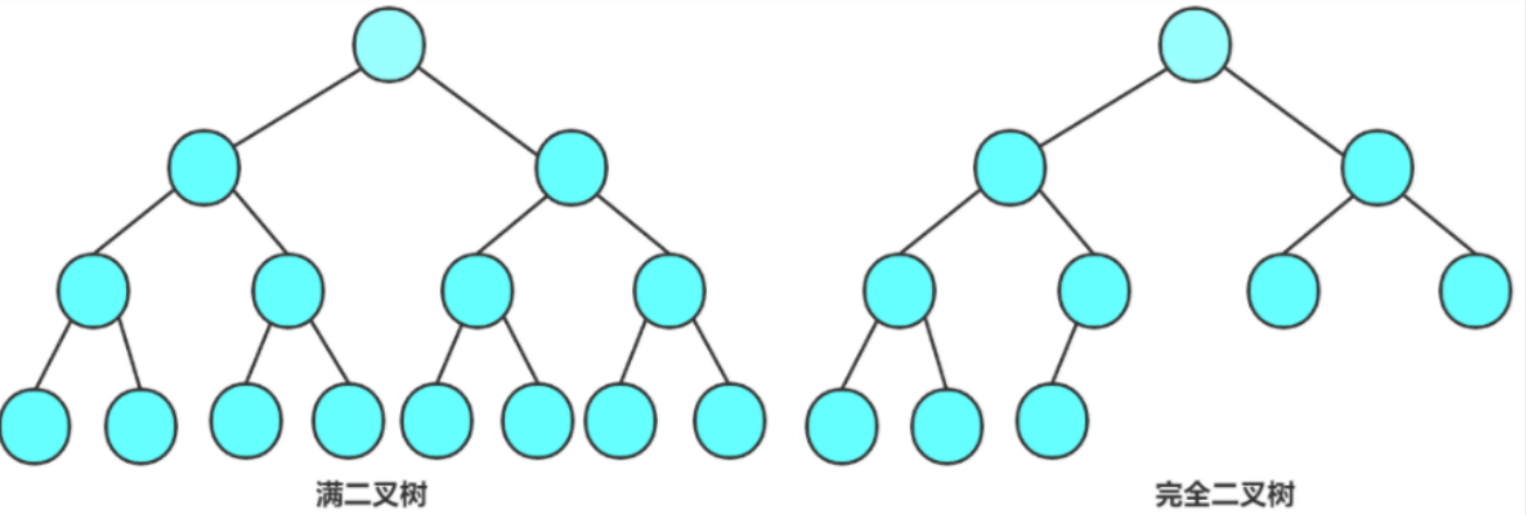
- 满二叉树:一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是 2 k − 1 2^k - 1 2k−1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
![在这里插入图片描述]()
二叉树的性质
-
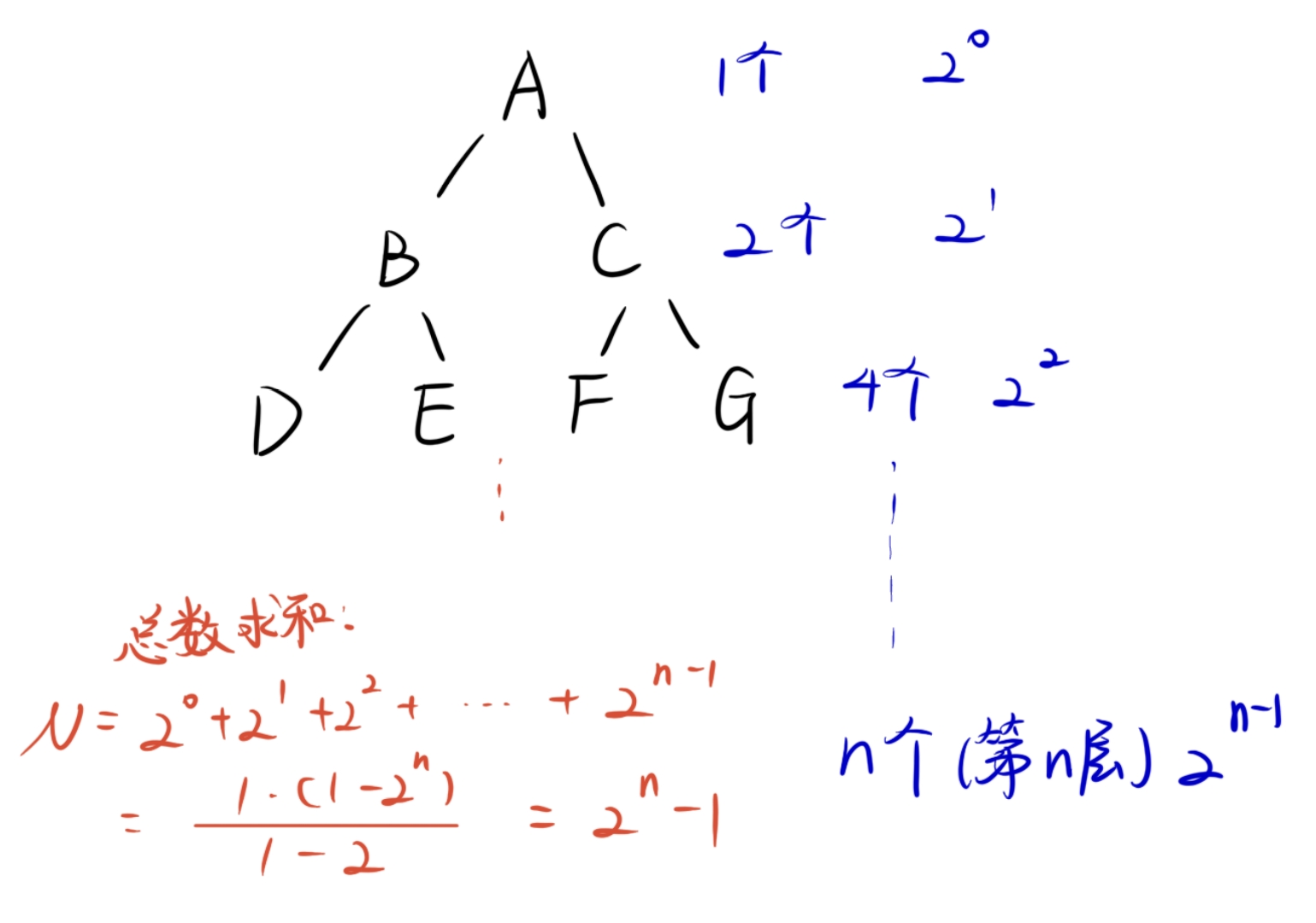
若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有: 2 i − 1 2^{i - 1} 2i−1( i > 0 i>0 i>0)个结点(找规律)
-
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点总数是: 2 k − 1 2^k - 1 2k−1( k > = 0 k>=0 k>=0)
-
对任何一棵二叉树,如果其叶结点个数为 n 0 n_0 n0,度为2的非叶结点个数为 n 2 n_2 n2,则有: n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1
-
具有n个结点的完全二叉树的深度k为: ⌈ log 2 ( n + 1 ) ⌉ \lceil\log_2(n + 1)\rceil ⌈log2(n+1)⌉(上取整)
-
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若 i > 0 i>0 i>0,双亲序号: ( i − 1 ) / 2 (i - 1)/2 (i−1)/2; i = 0 i=0 i=0, i i i为根结点编号,无双亲结点
- 若 2 i + 1 < n 2i + 1 < n 2i+1<n,左孩子序号: 2 i + 1 2i + 1 2i+1,否则无左孩子
- 若 2 i + 2 < n 2i + 2 < n 2i+2<n,右孩子序号: 2 i + 2 2i + 2 2i+2,否则无右孩子
概念练习题
-
某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()
-
A 不存在这样的二叉树
-
B 200
-
C 198
-
D 199
n0=n2+1=199+1=200,选B -
在具有 2n 个结点的完全二叉树中,叶子结点个数为()
-
A n
-
B n+1
-
C n-1
-
D n/2
![在这里插入图片描述]()
选A -
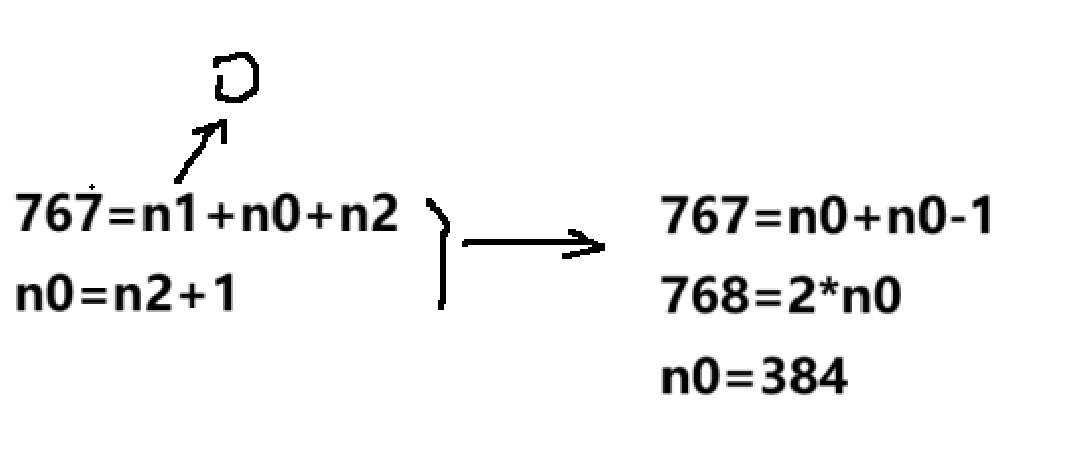
一个具有767个节点的完全二叉树,其叶子节点个数为()
-
A 383
-
B 384
-
C 385
-
D 386
![在这里插入图片描述]()
-
一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
-
A 11
-
B 10
-
C 8
-
D 12
-
我们可以根据完全二叉树的节点数与高度的关系来求解。
-
完全二叉树高度与节点数的关系 对于深度为 h h h的完全二叉树,节点数 n n n满足: 2 h − 1 ≤ n < 2 h 2^{h - 1} \leq n < 2^h 2h−1≤n<2h。
推导过程 已知完全二叉树的节点数 n = 531 n = 531 n=531。 我们需要找到满足 2 h − 1 ≤ 531 < 2 h 2^{h - 1} \leq 531 < 2^h 2h−1≤531<2h的 h h h。
计算可得: 2 9 = 512 2^9 = 512 29=512, 2 10 = 1024 2^{10} = 1024 210=1024。 因为 2 9 = 512 ≤ 531 < 1024 = 2 10 2^9 = 512 \leq 531 < 1024 = 2^{10} 29=512≤531<1024=210,所以 h − 1 = 9 h - 1 = 9 h−1=9, h = 10 h = 10 h=10。所以这棵完全二叉树的高度为 10,答案选 B。
-
二叉树的存储(开始代码实现)
- 二叉树的本质是链表的实现,所以与链表链表的起始创建一致
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
手动创建(非正式创建):
public void createBinaryTree(){
BTNode node1 = new BTNode(1);
BTNode node1 = new BTNode(2);
BTNode node1 = new BTNode(3);
BTNode node1 = new BTNode(4);
BTNode node1 = new BTNode(5);
BTNode node1 = new BTNode(6);
root = node1;
node1.left = node2;
node2.left = node3;
node1.right = node4;
node4.left = node5;
node5.right = node6;
}
☆二叉树的遍历
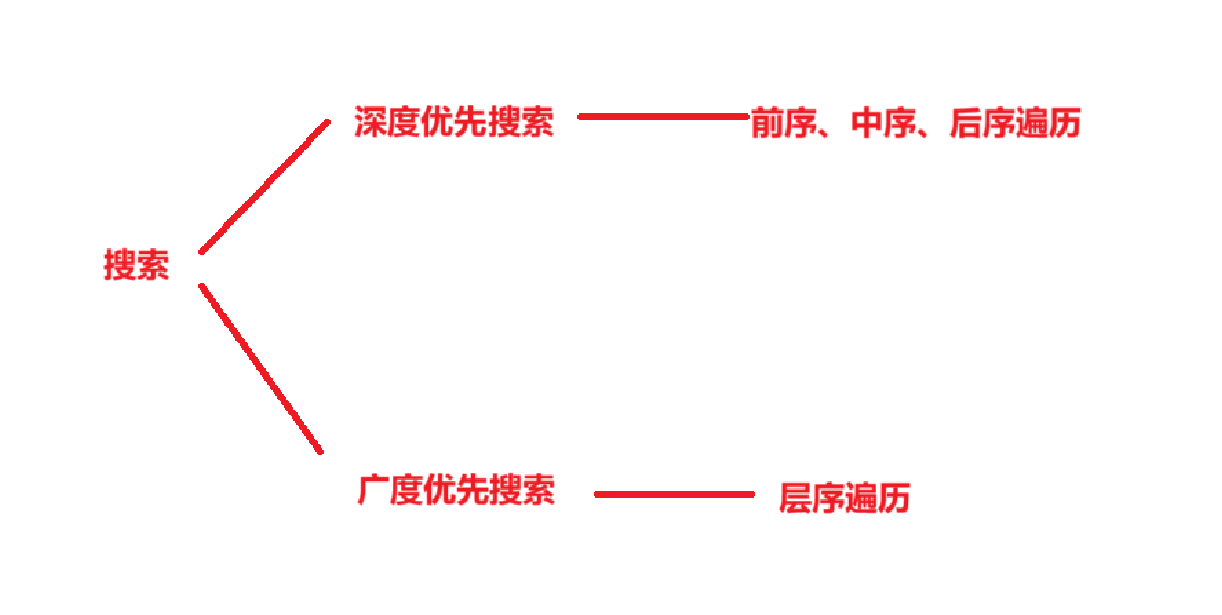
前中后序遍历
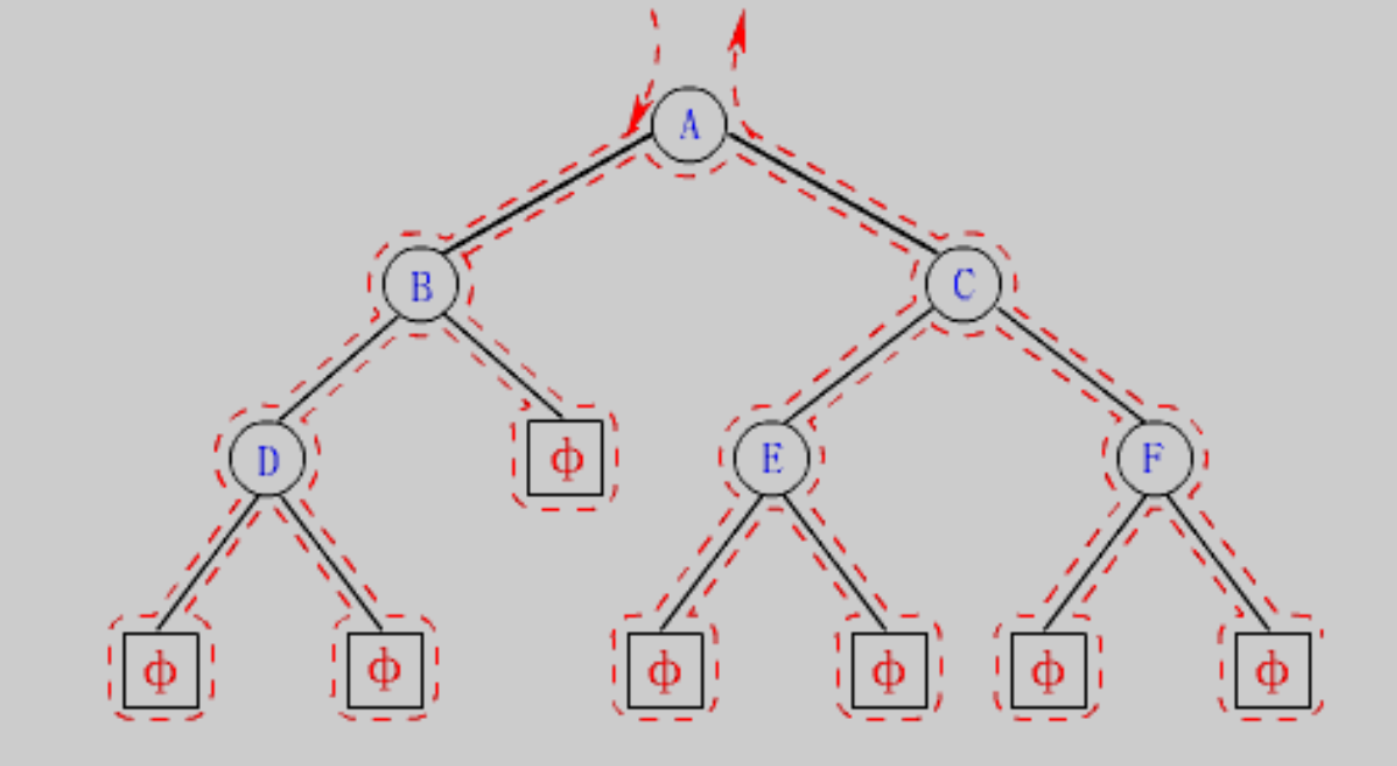
-
学习⼆叉树结构,最简单的⽅式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做⼀次且仅做⼀次访问。核心:通过递归实现
![在这里插入图片描述]()
-
前序遍历——根,左,右
// 前序遍历
public void preOrder(TreeNode root) {
if(root==null){
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
- 中序遍历——左,根,右
// 中序遍历
public void inOrder(TreeNode root) {
if(root==null){
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
- 后序遍历——左,右,根
// 后序遍历
public void postOrder(TreeNode root) {
if(root==null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}
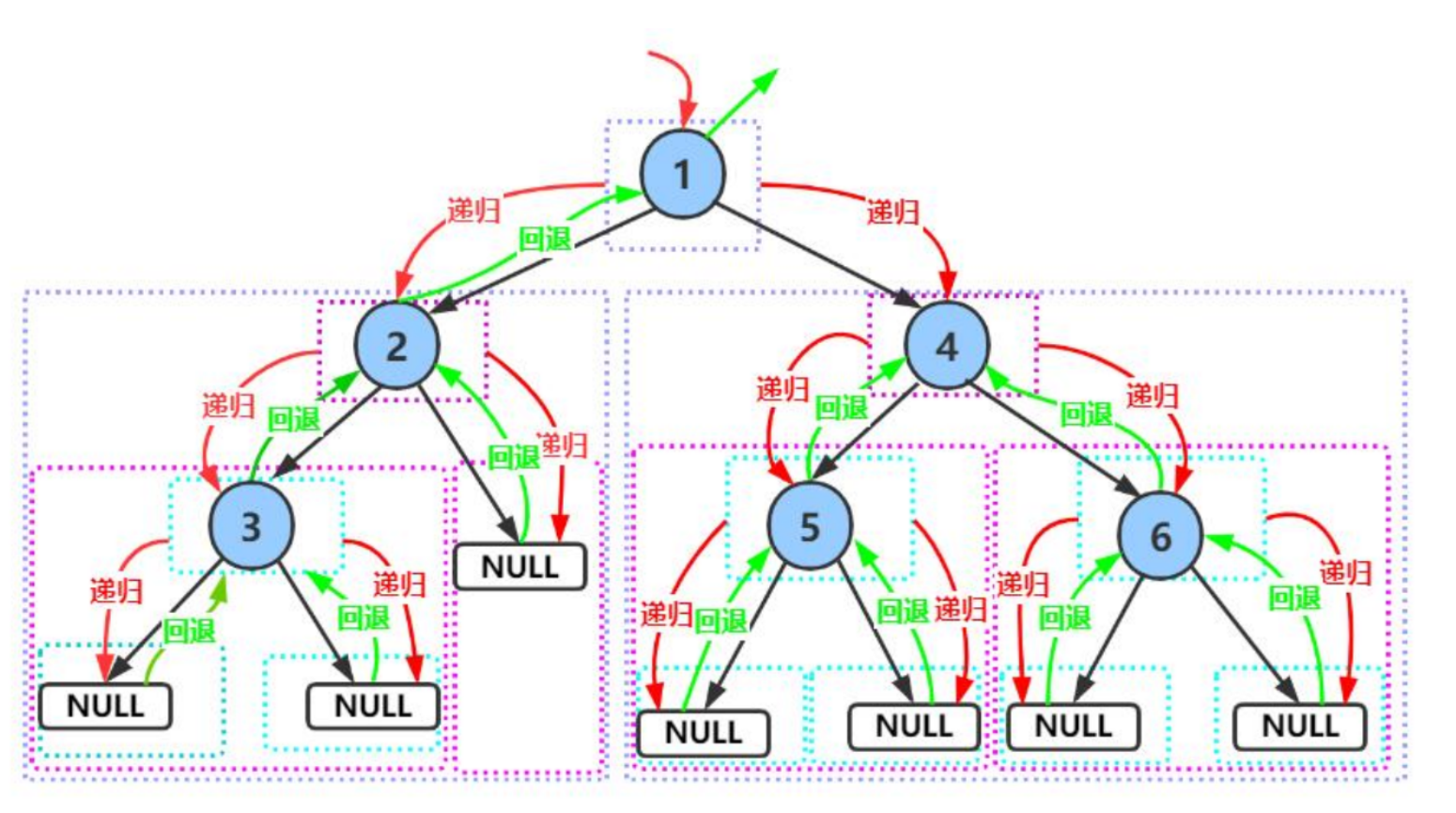
层序遍历
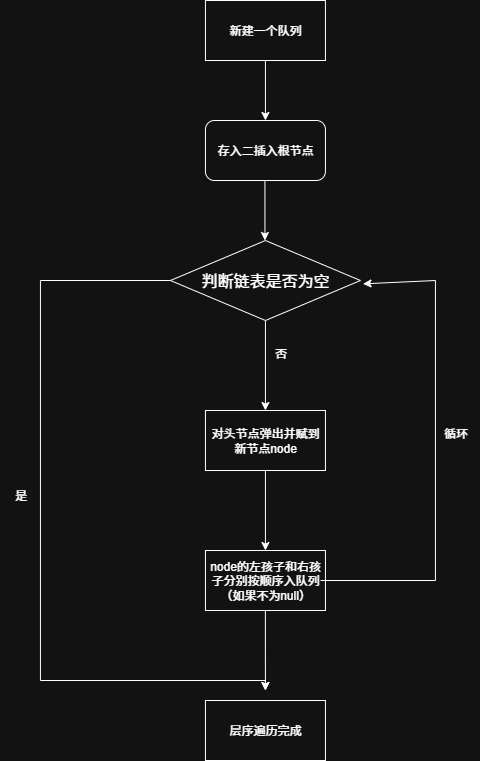
//层序遍历1
public void levelOrder(TreeNode root){
if(root==null){
return;
}
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.print(node.val+" ");
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
二维链表书写方式:
思路一致,只是把每一层单独存放最后统一汇总,需要有计数器来计每一层的节点个数
力扣—102. 二叉树的层序遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<List<Integer>>();
if (root == null) {
return ret;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<Integer>();
int currentLevelSize = queue.size();
for (int i = 1; i <= currentLevelSize; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
ret.add(level);
}
return ret;
}
}
基本操作
- 获取数中的节点个数
// 获取树中节点的个数
//计数器写法
public int nodeSize=0;
public void size(TreeNode root) {
if(root==null){
return;
}
nodeSize++;
size(root.left);
size(root.right);
}
//子问题思路
public int size2(TreeNode root) {
if(root==null){
return 0;
}
return size2(root.left)+size2(root.right)+1;
}
- 获取叶子结点的个数
// 获取叶子节点的个数
public int getLeafNodeCount(TreeNode root){
if(root == null) {
return 0;
}
if(root.left == null && root.right == null){
return 1;
}
return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}
- 获取第K层节点的个数
// 获取第K层节点的个数
public int getKLevelNodeCount(TreeNode root,int k){
if(root == null){
return 0;
}
if(k==1){
return 1;
}
return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);
}
- 获取⼆叉树的⾼度
// 获取⼆叉树的⾼度
public int getHeight(TreeNode root){
if(root == null){
return 0;
}
return Math.max(getHeight(root.left),getHeight(root.right))+1;
}
- 检测值为value的元素是否存在
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, int val){
if(root==null) {
return null;
}
if(root.val==val) {
return root;
}
TreeNode ret=find(root.left,val);
if(ret!=null) {
return ret;
}
ret=find(root.right,val);
if(ret!=null) {
return ret;
}
return null;
}




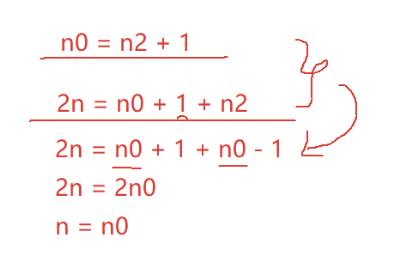

 浙公网安备 33010602011771号
浙公网安备 33010602011771号