动态规划总结（1）

动态规划（DP）总结（1）

*解决思路

1.dfs→2.记忆化搜索→3.递推（最终样式）

第一步和第二步推出状态转移方程后基本上题目可以解决

理解下面三条：

1. 最优化原理（最优子结构性质）

最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。

【子问题取最优，最终的大问题必然最优】

2. 无后效性

将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。

【顺序枚举每个物品（dfs次序），不会出现未来还会回头考虑之前的物品，保证了无后效性】

3. 子问题的重叠性

动态规划算法的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受，而搜索算法在时间上却无法承受，所以我们舍空间而取时间。

【记忆化搜索解决了子问题的重叠产生的时间浪费，即空间换时间】

*附题目代码/思路图

打家劫舍

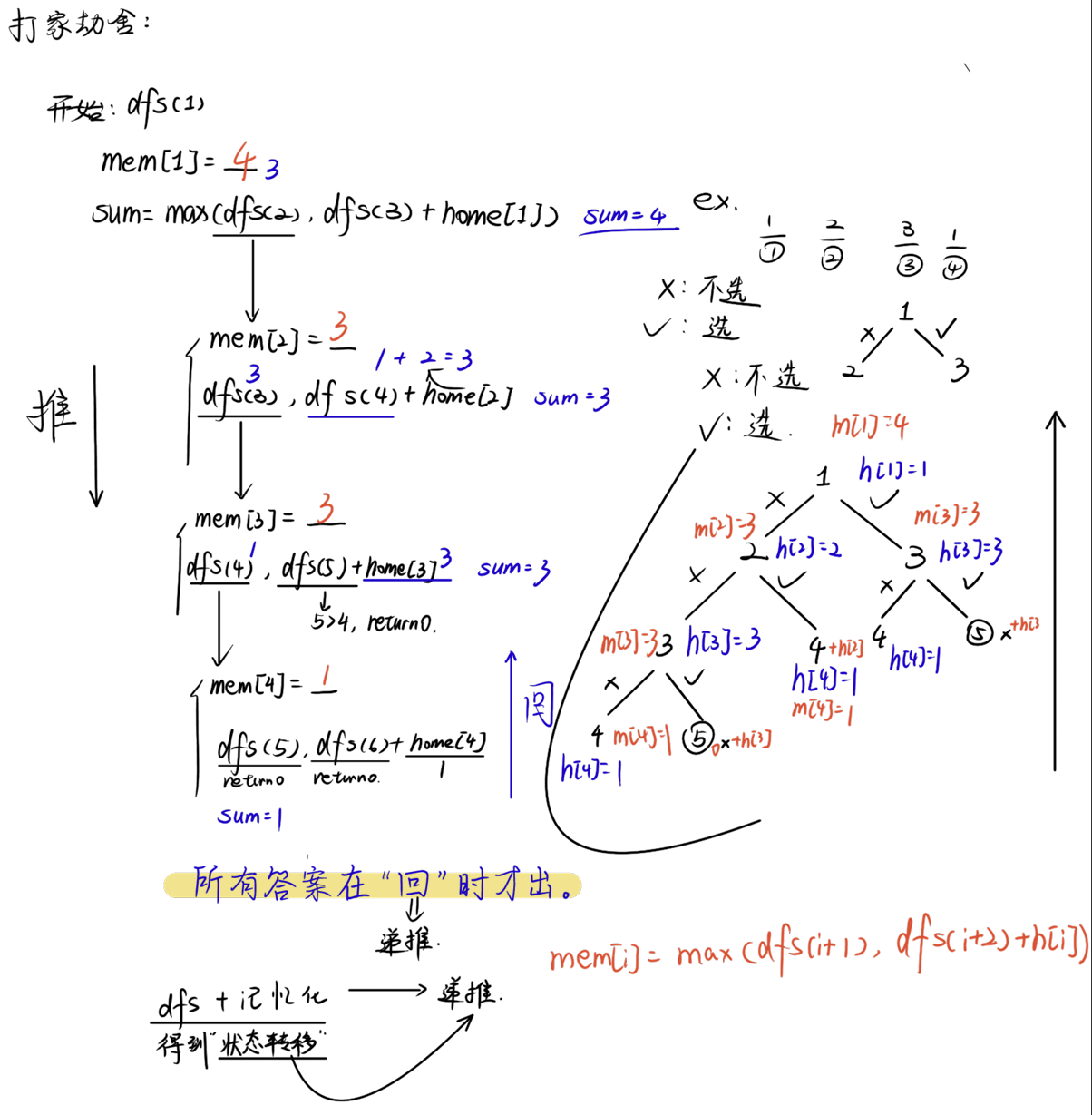
//https://leetcode.cn/problems/house-robber/description/?envId=2cktkvj&envId=2cktkvj
#include <bits/stdc++.h>
using namespace std;
const int N=10010;
int n,T;
int home[N];
int mem[N];
int f[N];
int dfs(int x)
{
    if(mem[x]) return mem[x];
    int sum=0;
    if(x>n) return sum=0;
    else
        sum=max(dfs(x+1),dfs(x+2)+home[x]);
    mem[x]=sum;
    return sum;
}
//mem[i]存的是：从第i个店铺开始（i~n）能获取的最大价值
int main()
{
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            cin>>home[i];
        }
//        memset(mem,0, sizeof(mem));
//        int res=dfs(1);
//        cout<<res<<endl;
        memset(f,0,sizeof(f));
        for(int i=n;i>=1;i--)
        {
            f[i]=max(f[i+1],f[i+2]+home[i]);//递推的公式就是递归向下的公式
        }
        cout<<f[1]<<endl;
    return 0;
}

//力扣核心代码模式版本

//dfs+记忆化搜索（会超时）
const int N=1010;
class Solution {

    int f[N];  
    int mem[N];
    int dfs(int x,vector<int>& nums)
    {
        if(mem[x]) return mem[x];
        int sum=0;
        if(x>nums.size()-1) return sum=0;
        else
            sum=max(dfs(x+1,nums),dfs(x+2,nums)+nums[x]);
        mem[x]=sum;
        return sum;
    }  
public:
    int rob(vector<int>& nums) {
        memset(mem,0, sizeof(mem));
        int res=dfs(0,nums);
        return res;
    }
};


//改递推
const int N=1010;
class Solution {
    int f[N];    
public:
    int rob(vector<int>& nums) {
        memset(f,0,sizeof(f));
        for(int i=nums.size()-1;i>=0;i--)
        {
            f[i]=max(f[i+1],f[i+2]+nums[i]);
        }
        return f[0];
    }
};

数字三角形

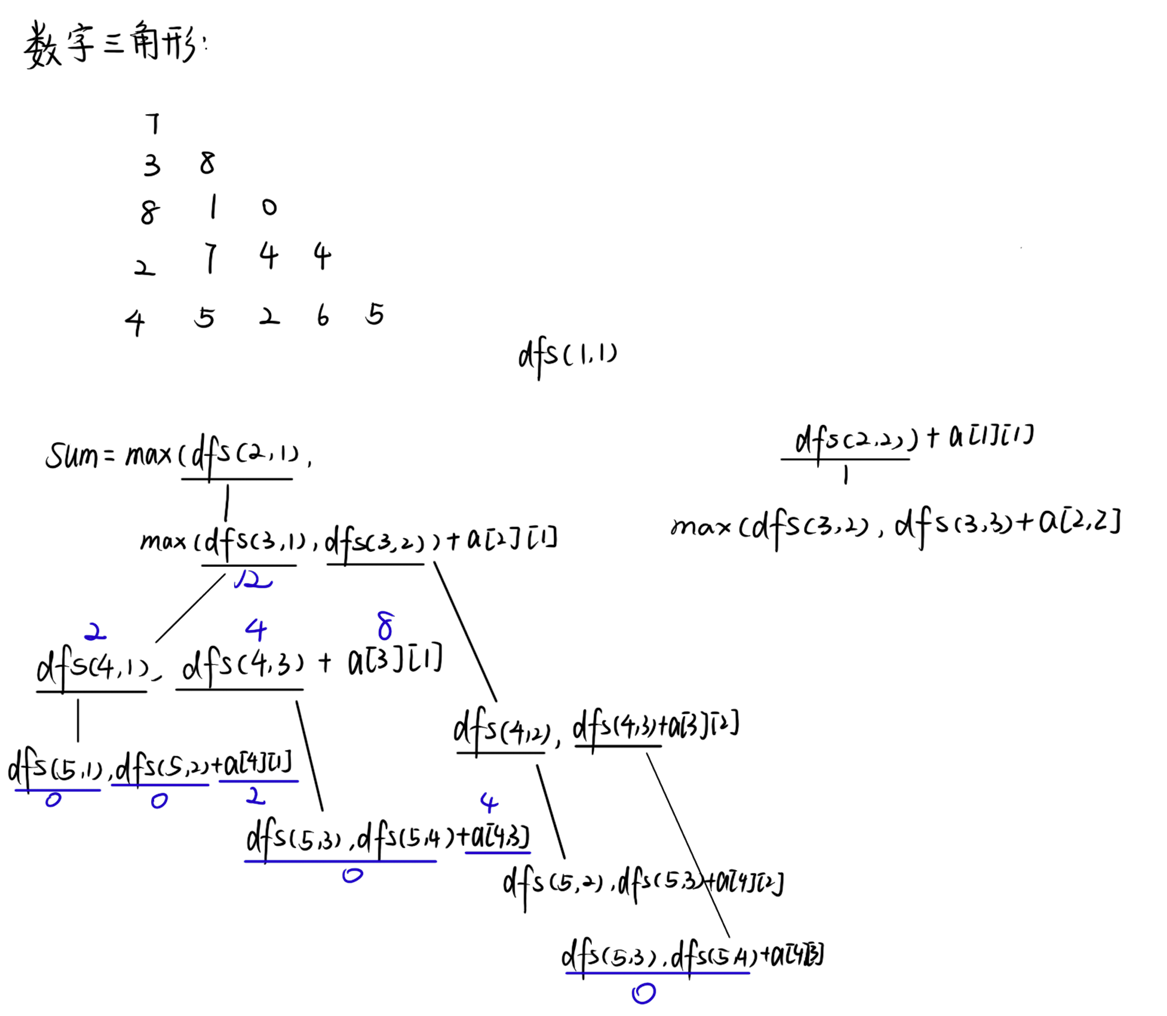
//https://www.luogu.com.cn/problem/P1216
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N][N];
int n;
int mem[N][N];
int f[N][N];
int dfs(int x1,int y1)
{
    if(mem[x1][y1])
        return mem[x1][y1];
    int sum=0;
    if(x1>n||y1>n)
        return 0;
    else
        //求子问题：dfs(x)=dfs(x+1)+dfs(x+2)
        //求最优子问题：dfs(x)=max(dfs(x+1),dfs(x+2))+a[x][y]
        sum= max(dfs(x1+1,y1),dfs(x1+1,y1+1))+a[x1][y1];
    mem[x1][y1]=sum;
    return sum;
}

int main() {
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for (int j = 1; j <=i ; j++) {
            cin>>a[i][j];
        }
    }

//    for (int i = n; i >=1 ; i--) {
//        for (int j = 1; j <=i ; j++) {
//            f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j];
//        }
//    }


    return 0;
}

最小费用爬楼梯

//https://leetcode.cn/problems/min-cost-climbing-stairs/
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
vector<int> a;
int mem[N];
int dfs(int x)
{
    if(x>a.size()) return 0;
    int sum=0;
    if(mem[x]!=-1) return mem[x];
    else
        sum=min(dfs(x+1),dfs(x+2))+a[x];
    mem[x]=sum;
    return sum;
}
int main()
{
    memset(mem,-1,sizeof(mem));
    int x;
    while(cin>>x)
    {
        a.push_back(x);
    }
    int res=min(dfs(0),dfs(1));
    cout<<res<<endl;
    return 0;
}

//力扣核心代码模式
const int N = 1010;
class Solution {
    int mem[N];
public:

    int dfs(int x, vector<int>& a) {
        if (x >= a.size()) return 0; // 如果超出数组范围，返回0
        if (mem[x] != -1) return mem[x];
        
        int sum = min(dfs(x + 1, a), dfs(x + 2, a)) + a[x]; // 当前台阶的花费加上下一步最小花费
        mem[x] = sum;
        return sum;
    }

    int minCostClimbingStairs(vector<int>& cost) {
        memset(mem, -1, sizeof(mem));
        return min(dfs(0, cost), dfs(1, cost)); // 从下标为0或1的台阶开始爬楼梯
    }
};

比较点

打家劫舍的状态转移方程

sum=max(dfs(x+1),dfs(x+2)+home[x]);

数字三角形、最小费用爬楼梯的状态转移方程

sum= max(dfs(x1+1,y1),dfs(x1+1,y1+1))+a[x1][y1]

sum=min(dfs(x+1),dfs(x+2))+a[x]