杂题选写

Last UPD on 2024/11/12

CF1667C Half Queen Cover

*2400

标签：构造；数学

题目大意

给定一个 \(n\times n\) 的棋盘，求出一个最小 \(k\) 使得可以通过在棋盘上放置 \(k\) 个皇后，且使得棋盘上所有位置都能被攻击。输出方案。

注意，皇后 \((x,y)\) 可以攻击到 \((X,Y)\) 当且仅当 \(x=X\) 或 \(y=Y\) 或 \(x-y=X-Y\)。

数据范围：\(1\le n\le10^5\)。

思路

让我们来考虑答案的下界。假设我们放置了 \(k\) 个棋子。

首先，这 \(k\) 个棋子可以覆盖 \(k\) 行 \(k\) 列，我们将剩下的行和列平移拼成一个 \((n-k)\times (m-k)\) 的矩阵。

此时，我们需要保证这个矩阵的 \(2(n-k)-1\) 条对角线都要有棋子覆盖，于是有 \(k\ge 2(n-k)-1\)，得到 \(k\ge\frac{2n-1}{3}\)。

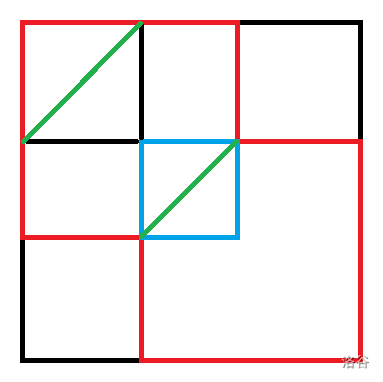
考虑当 \(n\bmod3=2\) 时，我们先将 \((n-k)\times(n-k)\) 的矩阵分别放在左上角和右下角然后再在左上角正方形的对角线和中间重叠正方形的对角线上放棋子即可。

若 \(n\bmod3\not=2\)，再在右下角补上一个棋子即可。

CF1906L Palindromic Parentheses

*2500

标签：构造

题目大意

构造一个长度为 \(n\) 的合法括号序列 \(s\)，满足其中最长的回文子序列的长度为 \(k\)。

数据范围：\(2\le n\le 2000\)，\(1\le k\le n\)。

思路

让我们来开一下 \(n=10\) 的情况：

先让我们考虑一个串 ((((()))))，我们可以构造出解的下界 \(\frac{n}{2}=5\)。

再考虑串 ()(((())))，此时答案变为 \(\frac{n}{2}+1=6\)。

若此时我们继续往左边添加 () 得到 ()()((()))，此时答案为 \(\frac{n}{2}+2=7\)。

但是当我们再添加一个 () 得到 ()()()(())，此时答案仍然为 \(7\)。

为什么？可以发现，当我们添加一个 () 后，会多一个 ) 来匹配，从而导致答案加 \(1\)。而当我们添加三个 () 时，匹配的 ) 数量就不够了，所以答案仍然为 \(7\)。

所以，让我们往右边添加 () 得到 ()()(())()，此时答案为 \(\frac{n}{2}+3=8\)。

在左边添加 () 会多一个 ) 来匹配，而往右边添加 () 会多一个 ( 来匹配，这两者可以互相匹配，来解决括号不足的情况。

所以，我们可以得到一种构造方式，往两边添加 \(k-\frac{n}{2}\) 个 ()，且使两边添加的数量尽量平均。

当 \(n=k\) 时无解。

CF1917E Construct Matrix

*2500

标签：构造

题目描述

给你一个偶数 \(n\) 和一个整数 \(k\) 。构造一个由数字 \(0\) 和 \(1\) 组成的大小为 \(n \times n\) 的矩阵，满足：

• 矩阵中所有数字之和正好为 \(k\) ；
• 每一行的异或和相同；
• 每一列的异或和相同。

思路

对于这一道题，当 \(k\) 为奇数时无解。因为每一行的 \(1\) 的个数的奇偶性是相同的，而 \(n\) 又是偶数，所以当 \(k\) 为偶数时无解。

其次，当 \(k=2\) 和 \(k=n^2-2\) 时，只有当 \(n=2\) 时有解。先让我们来看 \(k=2\) 的情况，我们有三种方式来排列它：在同一行/列，此时必回有两行/列的异或和为 \(1\)，而当 \(n>2\) 时其它行/列的异或和为 \(0\)；此外，我们可以把它们放在不同行和不同列，此时必有两行和两列的异或和为 \(1\)，而其它行和列的异或和为 \(0\)，故只有在 \(n=2\) 时有解。\(k=n^2-2\) 同理。

接下来，让我们考虑 \(k\bmod 4=0\) 的情况，我们只需要选择若干 \(2\times 2\) 的子矩阵将它们全部填上 \(1\) 即可。

然后是 \(k\bmod 4=2\) 的情况。此时若我们填 \(2\times 2\) 的矩阵会导致最后多出两个 \(1\)。所以先让我们构造一个花费 \(6\) 个 \(1\) 的方案。具体的，让我们填充以下图案。

\(1\)	\(1\)	\(0\)
\(1\)	\(0\)	\(1\)
\(0\)	\(1\)	\(1\)

其他位置填上 \(2\times 2\) 的子矩阵即可。

注意到当 \(k=n^2-6\) 时，我们需要多填 \(4\) 个位置：

\(1\)	\(1\)	\(0\)	\(0\)
\(1\)	\(0\)	\(1\)	\(0\)
\(\color{red}1\)	\(1\)	\(1\)	\(\color{red}1\)
\(\color{red}1\)	\(0\)	\(0\)	\(\color{red}1\)

CF1917E Construct Matrix 改

让我们去掉 \(n\) 为偶数的限制，以下讨论的 \(n\) 均为奇数。

思路

我们只需要解决 \(k\) 为偶数的情况，因为在其它情况下我们可以通过反转矩阵的每一个位置来实现构造。

让我们令 \(n=2x+1\)。

首先，因为 \(k\) 为偶数，所以每一行的异或值必须为 \(0\)，也就是说，每行有最多 \(2x\) 个 \(1\)，所以一共最多只有 \(4x^2+2x\) 个 \(1\)，那么当 \(k>4x^2+2x\) 时无解。

先来构造 \(k=4x^2+2x\) 的情况。我们只需要将除了 \(x=y\) 的格子放上 \(1\) 即可。

接着我们按照 \(n\) 为偶数的做法可以构造出 \(k=4m\) 或 \(k=4m+2\) 的方案，其中 \(m \le x^2\)，也就是说我们可以构造出 \(4x^2+2\) 的方案。

接下来我们只需要构造 \(4x^2+2<k<4x^2+2x\) 的方案。

我们可以在 \(4x^2+2x\) 方案的基础上对对角线进行如下变换：

\(1\)	\(0\)
\(1\)	\(1\)

变成

\(0\)	\(1\)
\(0\)	\(0\)

若我们依次选择第 \(2,4,\dots,2x\) 行的对角线，每次可以使答案减少 \(2\)，可以覆盖 \([4x^2,4x^2+2x]\) 这个区间内的所有偶数。

结束。

Matrix Remake

题目描述

给你三个整数 \(n,m,k\)，请你构造一个 \(n\times m\) 的矩阵 \(A\) 满足以下限制：

• 对于所有 \(i,j(1\le i\le n,1\le j\le m)\) 都有 \(1\le A_{i,j}\le 2k\)。

• 对于所有 \(i(1\le i\le m)\) 都有 \(\sum_{p=1}^{n}A_{p,i}\) 的值为奇数。

• 对于所有 \(i,i^\prime(1\le i<i\le n)\) 都存在一个整数 \(j(1\le j\le m)\) 满足 \(A_{i,j}\not=A_{i^\prime,j}\)。

数据范围：\(1\le n\times m\le 2\cdot 10^6\)，\(1\le k\le 10^9\)。

CF1896F Bracket Xoring

标签：构造

*2600

题目描述

给定一个长度为 \(2n\) 的 \(01\) 串 \(s\)，你可以进行至多 \(10\) 次操作，每次操作你需要给出一个长度为 \(2n\) 的合法括号序列，然后对与每一个匹配的括号对在 \(s\) 上所对应的位置进行取反。

构造出一种使得 \(s\) 全部为 \(0\) 的方案，或报告无解。

思路

然我们来分析每次操作对于 \(s\) 的可能的变化。

首先，\(s_1\) 和 \(s_{2n}\) 一定会被操作，所以当 \(s_1\not=s_{2n}\) 时无解。

其次，每次一定会有偶数个位置被操作，所以若 \(s\) 中有奇数个 \(1\) 无解。

不妨先假设 \(s_1=1\)，若不是可以通过操作 ()()...() 来将整个 \(s\) 取反。

每次操作，我们可以选择相邻的两个 \(1\) 将它们匹配，并在这两个 \(1\) 之间的 \(0\) 的位置填上 ()，这样每个为 \(0\) 的位置都会被操作两次，每个为 \(1\) 的位置只会被操作一次。

但这必须保证每两个 \(1\) 之间有偶数个 \(0\)。

考虑这个该如何构造。

不妨假设现在我们需要让 \(s_i\) 和 \(s_{i+1}\) 相同（注意，不是改为 \(0\)）：

• 若它们本来就相同，我们直接放 ()。
• 若他们不同，我们可以通过放 (( 或者 )) 来使得它们相同。具体的，我们可以看前面是否有没有被匹配的括号，如果有就放 ))，没有就放 ((。并且我们可以知道，没被匹配的括号个数一定是偶数。

其中，第 \(2\) 种操作一定会有偶数次，不然就不满足 \(1\) 的个数为偶数次的条件了。

所以，我们至多会使用 \(3\) 步来使得 \(s\) 变为 \(0\)。

CF1227G Not Same

*2600

标签：构造

题目描述

给定大小为 \(n\) 的序列 \(a\) , 满足 \(1 \leqslant a_i \leqslant n\)。

你需要执行至多 \(n+1\) 次操作使得所有数变为 \(0\) ,每次操作你可以把一个子集的元素都 \(-1\) , 要求每次操作的子集互不相同。

思路

有这样一个构造：先将 \(a_i\) 从大到小排序，然后对于每一个 \(i\) 从第 \(a_i\) 行开始填数，若到底了就从第 \(1\) 行开始填。

这为什么是对的？假设在这样的构造下存在第 \(i\) 行和第 \(j\) 行是完全相同的。令 \(g_{i,j}\) 表示第 \(i\) 行第 \(j\) 列填的数，因为 \(a_i\le n\) 所以 \(g_{i,i+1}\) 一定为 \(0\)，那么因为第 \(i\) 行和第 \(j\) 行相同，那么 \(g_{j,i+1}\) 也为 \(0\)。

对于第 \(i+2\) 列，有 \(a_{i+2}\le a_{i+1}\)，所以这一列最下面的 \(1\) 只能在第 \(j\) 行及以上，但会因为第 \(i\) 行和第 \(j\) 行相同而不能在第 \(j\) 行，同理可得第 \(i+1\) 列到第 \(j-1\) 列的第 \(j\) 行均为 \(0\)，所以有 \(a_{j-1}=1\) 从而 \(a_j=1\)。但是第 \(i\) 行和第 \(j\) 行相同，所以 \(g_{i,j}=1\) 所以 \(a_j>1\)，于是矛盾。

CF1491G Switch and Flip

*2800

标签：思维；图论

题目描述

有 \(n\) 枚硬币。初始时，第 \(i\) 枚硬币在位置 \(c_i\) 上（\(c\) 是排列），正面朝上。你可以进行至多 \(n+1\) 次以下操作：

• 选择两个整数 \(i,j\)，然后交换硬币 \(i,j\)，并将硬币 \(i,j\) 翻面。

你需要使得第 \(i\) 枚硬币在位置 \(i\) 上且都是正面朝上。

数据范围：\(3\le n\le 2\times 10^5\)。

思路

我们将 \(i\) 向 \(c_i\) 连边，可以得到若干置换环。

我们称一次操作为交换 \(c_i\) 和 \(c_{c_i}\)。

那么一次操作就会让一个 \(a\to b\to c\) 变成 \(b\to c\) 和 \(a\to a\) 的自环，且 \(a,b\) 的颜色发生改变。

接下来让我们对于一个大小为 \(s\) 的环来单独考虑：第一次操作，我们随便选定一个 \(i\)，之后每次操作我们就将被翻了面的硬币作为 \(i\) 来操作，这样子我们可以用至多 \(s\) 次操作来让环上的点都到自己为位置上去，之后我们还需要若干次操作来使得每个硬币都是正面朝上，所以，若单独考虑一个环，它的操作次数至少为 \(s+1\)。显然，将每个环单独考虑的操作次数是不对的。

让我们考虑两个环 \(s1,s2\)，先用一次操作将两个环拼接在一起，此时环上有两枚反面硬币，接下来我们至多还可以使用 \(s1+s2-1=s-1\) 次操作。

同样是选择一个反面硬币来进行操作，最后再将两个反面硬币形成的环来一次操作就可以使得这两个环均满足条件。

若环的个数为偶数，我们就可以两两处理。

若环的个数为奇数，那么我们就可以把这个环和前面的一个自环相结合，会多产生一次操作次数。

接下来让我们考虑只有 \(1\) 个环的情况。

先考虑当 \(n=3\) 时，我们可以：

• \(c,a,b\)
• \(-a,-c,b\)
• \(-b,-c,a\)
• \(-b,-a,c\)
• \(a,b,c\)

花费 \(4\) 次操作。

若是一个 \(n>3\) 的环，我们先随便操作一个点，然后得到两个均含有一个反面硬币的环，而我们每次就需要对这个反面硬币进行操作。当其中一个环只剩下两个点时，我们就可以按照类似于 \(n=3\) 的方式来处理。

最后会花费 \(n+1\) 次操作。

CF702F T-shirts

*2800

标签：数据结构；贪心

题目描述

有 \(n\) 个物品，每个物品有两个属性 \((c_i,q_i)\)，分别表示物品的价格和质量。然后有 \(k\) 个人要来买物品，第 \(i\) 个人有 \(b_i\) 元。

每个人会优先选择能够购买且质量最大的物品购买，若质量一样就选择价格最小的。你需要求出每个人能购买多少物品。询问相互独立。

\(1\le n,k\le 2\cdot10^5\)，\(1\le c_i,q_i,b_i\le 10^9\)。

思路

质量几乎是没用的，我们只需要按照 \(q_i\) 先从大到小排序，然后按照顺序来依次选择物品。

我们有一个暴力的做法：对于每一个人，顺次枚举每一个物品看能不能选。但这个做法不是很有前途。

让我们考虑另一个暴力：我们来顺次枚举每一个物品，然后看有哪些人能够购买这个物品。

这个问题就相当于：给定一个序列 \(b\)，然后有 \(n\) 次操作，每次操作将所有不小于 \(c_i\) 的数减去 \(c_i\)。

这看上去很可以用数据结构来维护。考虑平衡树。

对于每一个物品 \(i\)，我们可以将当前所有人手上的钱划分为三个区间：\([0,c_i),[c_i,2c_i],(2c_i,+\infty)\)。

其中，第一个区间的数不会受到影响，第三个区间的数减去 \(c_i\) 后相对顺序不会改变，可以直接打标记来维护。

现在的问题是第二个区间，这个区间内的数减去 \(c_i\) 后，会改变其与第一个区间内数的顺序。

实际上，我们可以对第二个区间内的数暴力修改。因为这个区间里的数每次修改至少会减小一半，所以每个数被修改的次数为 \(\log_2 b_i\) 次。

AGC016D XOR Replace

*2902

标签：思维；图论

题目描述

现有一个序列，一次操作可以将某个位置变成整个序列的异或和。问最少几步到达目标序列。

\(1\le n\le 10^5,0\le a_i,b_i\le 2^{30}\)。

思路

神仙建图。

先让我们来考虑每次操作相当于什么。假设当前 \(a\) 的异或和为 \(x\)，那么一次操作就相当于选择一个 \(i\) 并将 \(a_i\) 和 \(x\) 进行交换。

然后我们可以按照以下方式来建边：若 \(a_i\not=b_i\) 则从 \(b_i\) 向 \(a_i\) 连接一条边。

若我们走了一条边 \(x\to a_i\)，那么就相当于将 \(x\) 移动到 \(a_i\)，并删除这条边。

但是很可能不存在这样一条边，此时可能会存在一条 \(y\to a_i\) 的边，这时我们就可以操作 \(a_i\) 将这条边变为 \(y\to x\)，然后将 \(x\) 移动到 \(a_i\)。

可以发现，第一个操作会使边数减少一，而第二个操作后边数不变。

而我们最终的目标就是删除所有的边。所以，我们要最小化操作二的数量。

令第 \(i\) 个连通块的大小为 \(siz_i\)。可以发现，对于 \(x\) 存在的连通块，我们可以通过 \(siz_i\) 次操作将这里的所有边都删除。

而对于不存在 \(x\) 的连通块，我们则需要通过一次操作二来将 \(x\) 移动到当前连通块中。

所以，答案就是边数加上连通块数量减一，但是若 \(x\) 单独成块，就不需要减一。

CF1713F Lost Array

*2900

标签：构造；数学

题目描述

给出一个从 \(1\) 到 \(n\) 的数组 \(a\)。有一个从 \(0\) 开始标号的大小为 \((n+1)\times (n+1)\) 的矩阵 \(b\)，通过以下方式生成：

• 对于 \(0 \le i \le n\)，\(b_{i,0} = 0\)。
• 对于 \(1 \le i \le n\)，\(b_{0,i} = a_{i}\)。
• 对于 \(1 \le i, j \le n\)，\(b_{i,j} = b_{i,j-1} \oplus b_{i-1,j}\)。

现在，给出 $ b_{1,n}, b_{2,n}, \ldots, b_{n,n} $，试还原出一个满足条件的 \(a\) 数组，或者报告无解。

思路

让我们考虑如何用 \(a\) 去构造出 \(b_{i,n}\)。

我们先将 \(a\) 贡献到对角线上，为了方便，我们将 \(a\) 和对角线均从有往左编号 \(0\) 到 \(n-1\)。

我们发现，当 \(C_i^j\bmod 2=1\) 时 \(a_i\) 才会对 \((j,j)\) 造成贡献，而我们知道当 \(j\) 在二进制下是 \(i\) 的子集是才满足这个条件，证明可以用卢卡斯定理。

同理，我们也可以求出对角线对 \(b\) 的贡献。所以我们只需要对 \(b\) 做一次子集和的逆再做一次超集和的逆即可还原 \(a\)。

而因为这是异或运算，所以子集和的逆即为子集和，超集和的逆即为超集和。

CF2021E Digital Village

*2300/2500/2800

标签：动态规划；dp 优化；闵可夫斯基求和；Kruskal 重构树；贪心；长链剖分

题目描述

给定一张有 \(n\) 个点和 \(m\) 条边的图，边有边权。你需要选择 \(k\) 个点并将它们标记为特殊点，然后给定 \(q\) 个关键点，并给每个关键点分配一条到特殊点的路径。

定义一个关键点的权值为该路径上边权的最大值。最小化所有关键点的权值和。你需要对于每一个 \(k=1,2\dots,n\) 分别求出答案。

数据范围：

• E1：\(1\le n,m\le 500\)。
• E2：\(1\le n,m\le 5000\)。
• E3：\(1\le n,m\le 2\times10^5\)。

思路

让我们把该图的 Kruskal 重构树先建出来。此时所有原图中的点都变为叶子节点，边权转移到了点上。

令 \(dp_{i,j}\) 表示到了第 \(i\) 个点，选了 \(j\) 个特殊点的最小权值和，于是有转移：

\[dp_{i,x+y}=\min\begin{cases} dp_{ls,x}+dp_{rs,y}+tot_{ls}\times w_i & x=0,y>0\\ dp_{ls,x}+dp_{rs,y}+tot_{rs}\times w_i & x>0,y=0\\ dp_{ls,x}+dp_{rs,y} & otherwise \end{cases} \]

其中，\(tot_i\) 表示在 \(i\) 的子树中关键点的数量。也就是说，若在一个子树内我们没有给任何一个叶子设成关键点，那么用当前边来造成贡献，使得它们满足条件。

初值有 \(dp_{i,0}\) 和 \(dp_{i,1}\) 为 \(0\)，其它设为极大值。

然后我们就可以在 \(O(n^2)\) 的复杂度内解决 E2。

容易发现，对于一个 \(i\)，它所对应的 \(dp_i\) 是凸的，不难用归纳法证明。于是可以用闵可夫斯基求和来解决。

实现时，直接插入这次多出来的那一段即可。

时间复杂度 \(O(n\log^2n)\)，可以通过 E3。

PS：还有一种做法是转化问题后贪心，然后用左偏树维护，类似于 BZOJ3252 攻略。

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const ll inf = 1e16;
int n, m, p, id[200005];
bool flg[200005];
int fa[200005], siz[200005], sizp[200005];
ll sum[200005];
priority_queue<ll, vector<ll>, greater<ll> > q[200005];
void merge(int u, int v) {
    if(q[id[u]].size() < q[id[v]].size()) swap(u, v);
    while(!q[id[v]].empty()) q[id[u]].push(q[id[v]].top()), q[id[v]].pop();
    id[v] = id[u];
}
int FindSet(int x) {return fa[x] == x ? x : fa[x] = FindSet(fa[x]);}
struct edge {
	int u, v, w;
	bool operator <(const edge &t) const {return w < t.w;}
} arr[200005];
void solve() {
	scanf("%d %d %d", &n, &m, &p);
	for(int i = 1; i <= n; i++) {
		flg[i] = false;
		while(!q[i].empty()) q[i].pop();
	}
	for(int i = 1, x; i <= p; i++) scanf("%d", &x), flg[x] = true;
	for(int i = 1; i <= m; i++) scanf("%d %d %d", &arr[i].u, &arr[i].v, &arr[i].w);
	sort(arr + 1, arr + m + 1);
	for(int i = 1; i <= n; i++) fa[i] = i, siz[i] = 1, sizp[i] = flg[i], q[id[i] = i].push(0), sum[i] = 0;
	for(int i = 1; i <= m; i++) {
		int u = FindSet(arr[i].u), v = FindSet(arr[i].v);
		if(u == v) continue;
		fa[u] = v;
		ll tmpl = q[id[u]].top(), resl = 1ll * sizp[u] * arr[i].w - sum[u]; q[id[u]].pop(), q[id[u]].push(tmpl - resl); sum[u] += resl;
		ll tmpr = q[id[v]].top(), resr = 1ll * sizp[v] * arr[i].w - sum[v]; q[id[v]].pop(), q[id[v]].push(tmpr - resr); sum[v] += resr;
		merge(u, v);
		siz[v] += siz[u], sizp[v] += sizp[u], sum[v] += sum[u];
	}
	int rot = FindSet(1); 
	ll ans = 0;
	for(int i = 1; i <= n; i++) {
		ans += q[id[rot]].top();
		printf("%lld ", sum[rot] + ans); 
		q[id[rot]].pop();
	}
	puts("");
}
int main() {
	int t; cin>>t;
	while(t--) solve();
	return 0;
}

CF2003F Turtle and Three Sequences

*2800

标签：状态压缩；动态规划；随机化（color-coding）；dp 优化

题目描述

有三个序列 \(a_1, a_2, \ldots, a_n\)，\(b_1, b_2, \ldots, b_n\) 和 \(c_1, c_2, \ldots, c_n\) 。

需要选择长度为 \(m\) 的 \(1, 2, \ldots, n\) 的子序列，记为 \(p_1, p_2, \ldots, p_m\)。并且满足以下条件：

• \(a_{p_1} \le a_{p_2} \le \cdots \le a_{p_m}\);
• 所有索引 \(i\) 的所有 \(b_{p_i}\) 都是两两不同，即不存在两个不同的索引 \(i\)，\(j\) 使得 \(b_{p_i} = b_{p_j}\) 。

找出 \(\sum\limits_{i = 1}^m c_{p_i}\) 的最大值。

思路

https://www.cnblogs.com/ddxrS/p/18430320

CF208E Blood Cousins 改 / Cnoi2019 雪松果树

标签：dfs；差分

题目描述

有两种询问：

• 求出一个节点 \(u\) 的 \(k\) 级祖先。
• 求出一个节点 \(u\) 的 \(k\) 级子孙数量。

你需要在时空均为 \(O(n+q)\) 的复杂度内解决。

思路

我们可以离线来处理所有询问。

先考虑第一个问题：求 \(u\) 的 \(k\) 级祖先。我们只需要用 dfs 来遍历这棵树，并且用一个栈来实时维护祖先对应的信息。

求出一个节点的 \(k\) 级子孙数量。在树上差分，用类似于 (NOIP2016 提高组) 天天爱跑步 的方法。我们只需要记录下在进入 \(u\) 的子树前每个深度的数量，然后再用遍历完 \(u\) 子树后减去遍历子树前的值，即可得出答案。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, q, fa[N], cnt[N], ans[N];
vector<int> E[N];
vector<pair<int, int> > que[N], in[N];
void dfs1(int x, int dep) {
	fa[dep] = x; for(auto p : in[x]) if(dep >= p.first) que[fa[dep - p.first]].push_back(make_pair(dep, p.second)); else ans[p.second] = 1;
	for(auto y : E[x]) dfs1(y, dep + 1);
}
void dfs2(int x, int dep) {
	for(auto p : que[x]) ans[p.second] -= cnt[p.first];
	cnt[dep]++; for(auto y : E[x]) dfs2(y, dep + 1);
	for(auto p : que[x]) ans[p.second] += cnt[p.first];
}
int main() {
	scanf("%d %d", &n, &q);
	for(int i = 2, x; i <= n; i++) scanf("%d", &x), E[x].push_back(i);
	for(int i = 1, a, b; i <= q; i++) scanf("%d %d", &a, &b), in[a].push_back(make_pair(b, i));
	dfs1(1, 0), dfs2(1, 0);
	for(int i = 1; i <= q; i++) printf("%d ", ans[i] - 1);
	return 0;
}

CF2021D Boss, Thirsty

*2500

tag：动态规划

题目描述

给定一个 \(n\times m\) 的矩阵 \(A\)。

对于矩阵的第 \(i\) 行，你需要选出一个区间 \(l_i,r_i\) 并获得 \(\sum_{j=l_i}^{r_i} A_{i,j}\) 的利润，且你选出的区间需要满足：

• 对于 \(2\le i\le n\)，均有区间 \([l_{i-1},r_{i-1}]\) 和 \([l_i,r_i]\) 相交；
• 对于 \(2\le i\le n\)，均满足区间 \([l_{i-1},r_{i-1}]\) 不包含 \([l_i,r_i]\)。

最大化你选出的利润和。

思路

https://www.cnblogs.com/ddxrS/p/18457534

CF1707E Replace

*3500

tag：倍增，思维

题目描述

给定一个长为 \(n\) 的序列 \(a_1,\ldots,a_n\)，其中对于任意的 \(i\) 满足 \(1 \leq a_i \leq n\)。

定义一个二元组函数如下：

\[f((l,r))=(\min\{a_l,\ldots,a_r\},\max\{a_l,\ldots,a_r\})(l \leq r) \]

你需要回答 \(q\) 次询问，每次给定 \((l_i,r_i)\)，问其最少经过多少次 \(f\) 的调用（即 \((l,r) \rightarrow f((l,r))\)）使得 \((l_i,r_i)\) 变成 \((1,n)\)，若无解请输出 -1。

思路

模拟赛 T4，然后发现之前做过。

令将区间 \([l,r]\) 进行 \(k\) 次变换后的区间记为 \(f^k(l,r)\)。每次询问我们要求的就是一个最小的 \(k\) 使得 \(f^k(l,r)=[1,n]\)。

可以考虑倍增，即只求出 \(f^{2^k}(l,r)\)，每次询问从大到小来枚举 \(2^k\)。可以在 \(O(\log n)\) 的复杂度内得出答案。

但是这样做我们就需要提前预处理出 \(O(n^2)\) 个区间，复杂度还是不对。

但是这里有一个性质：若区间 \([l_1,r_1]\) 和区间 \([l_2,r_2]\) 满足 \([l_1,r_1]\cup [l_2,r_2]=[l,r]\) 且 \([l_1,r_1]\cap[l_2,r_2]\not=\emptyset\)，那么有 \(f^k(l_1,r_1)\cup f^k(l_2,r_2)=f^k(l,r)\)。

不难用归纳法证出。

由此性质，我们只需要预处理出 \(f^k(i,i+1)\) 就可以推出所有区间的答案。

具体可以使用 rmq + 倍增来维护。

CF1771F Hossam and Range Minimum Query

*2500

tag：主席树，随机化

题目描述

给定一个序列 \(a\)，\(q\) 次询问，求出区间 \([l,r]\) 中最小的出现次数为奇数的数。

思路

先考虑出现次数为奇数这个限制条件，发现我们可以使用异或来维护，若存在一个值域区间 \([L,R]\) 满足这个区间内所有出现的数的异或和不为 \(0\)，那么这个区间内必然存在一个出现次数为奇数的数。

所以，我们只需要先将所有数随机赋权，然后用主席树维护异或和，每次询问在主席树上二分即可。

CF1746F Kazaee

*2800

tag：数据结构，随机化

题目描述

支持两种操作：

• 将 \(a_i\) 设为 \(x\)。
• 询问 \([l,r]\) 中是否所有数的出现次数都为 \(k\) 的倍数。

思路

考虑随机赋权，然后求出区间和 \(s\)，若 \(k\mid s\) 则可能满足条件。

但这样正确率是不够的，当 \(k\) 较小时这个随机赋权很可能错误。

所以我们可以多随机几次，大概 \(30\) 次左右就可以了。

CF1136E Nastya Hasn't Written a Legend

*2200

tag：数据机构，线段树

题面描述

给定长为 \(n\) 的数组 \(a\)，长为 \(n-1\) 的数组 \(k\)。请支持 \(2\) 种操作：

1. + i x，表示 \(a_i \gets a_i + x\)，然后重复以下过程：若 \(a_{i+1} < a_i + k_i\)，则 \(a_{i + 1} \gets a_i + k_i,i \gets i + 1\)，否则结束本次操作。
2. s l r，输出 \(\sum\limits_{i = l}^r a_i\)。

思路

先让我们来考察 \(a_i\) 和 \(a_{i+1}\) 之间的关系：\(a_{i+1}<a_i+k_i\) 也就是 \(a_{i+1}-k_i<a_i\)，等价于 \(a_{i+1}-k_i-k_{i-1}-\dots-k_1<a_i-k_{i-1}-\dots-k_1\)。

令 \(f_i=\sum_{j=1}^i k_j\)，那么有 \(a_{i+1}-f_i<a_i-f_{i-1}\)。又可以发现对于每一个能被修改的 \(j=i+1,i+2,\dots\)，他们的 \(a_{j}-f_{j-1}\) 应该是单调的。

也就是说，我们只需要二分找到连续段的最后一个 \(a_{j}-f_{j-1}<a_i-f_{i-1}\) 的位置，那么区间 \([i,j]\) 都会被修改。

我们只需要用线段树维护 \(a_i-f_{i-1}\) 的值，每次修改就相当于将这个区间赋值为 \(a_i-f_{i-1}\)。

查询时直接查询区间和，再加上 \(\sum_{i=l}^{r}f_{i-1}\) 即可。

CF2025F Choose Your Queries

*2700

tag：思维

题目描述

初始有 \(n\) 个值为 \(0\) 的变量 \(a_1,a_2,\dots,a_n\)，然后有 \(q\) 次操作，每次操作给出两个 \(x,y\)，你需要选择 \(a_x\) 或 \(a_y\) 并将它 \(+1\) 或 \(-1\)。

你需要保证任意时刻每个变量的值都不小于 \(0\)。

最小化 \(q\) 次操作后所有变量的和。

思路

将每次操作看成一条无向边，每次操作我们相当于给边定向，每次将入的那个点进行操作，可以发现，若一个点的入度为奇数，那么这个点最后的值为 \(1\)，若为偶数，那么最后的值为 \(0\)。

所有我们的目标就是最小化入度为奇数的点的数量。

对于每一个连通块单独考虑。问题的下界是连通块中所有节点的度数和 \(\bmod 2\) 后的值，考虑构造到这个下界。

我们先把这个连通块的 dfs 树跑出来，对于非树边，我们先贪心的将所有指向父亲节点。

之后从叶子开始考虑每个点，若当前这个点的入度为奇数，就将这条树边指向自己，否则指向父亲。显然，最后只会有根节点的入度可能为奇数。

CF1929F Sasha and the Wedding Binary Search Tree

*2300

tag：组合数学，树形结构

题目描述

给定一棵二叉搜索树，其中一些节点已经点权，询问有多少种在剩余节点设置点权（值域 \([1,c]\)）的方案。

数据范围 \(1\le n\le 2\times n\)，\(1\le c\le 10^9\)。

思路

对于一棵二叉搜索树，我们将它中序遍历的序列跑出来，得到的点权序列一定是不递减的。

依次考虑每一个连续的 -1 的段 \([l,r]\)，只需要求出这一段有多少中填法，且值域在 \([a_{l-1},a_{r+1}]\) 之间，易知答案为 \(C_{a_{r+1}-a_{l-1}-(r-l+1)}^{r-l+1}\)。

由于 \(\sum (r-l+1)\) 只有 \(O(n)\)，所以时间复杂度 \(O(n\log n)\) 或 \(O(n)\)。

CF848C Goodbye Souvenir

*2600

tag：数据结构，树套树，分块，莫队，cdq 分治

题目描述

给定一个长度为 \(n\) 的序列 \(a\)，分别表示每个数的颜色。定义一种颜色在区间 \([l,r]\) 的贡献为：这种颜色最后出现的下标减去首次出现的下标。

支持两种操作，单点修改，区间查询所有颜色的权值和。

数据范围 \(n,m\le 10^5\)。

思路

直接计算每种颜色的贡献不太好算，让我们把贡献拆开：记 \(i\) 上一个与 \(i\) 颜色相同的数的下标为 \(lst_i\)，那么对于一次询问就相当于是求 \(\sum_{l\le pre_i,i\le r}(i-pre_i)\) 的值。

由于我们需要同时保证 \(pre_i\) 和 \(i\) 都在区间 \([l,r]\) 内，不妨将这看为一个二位数点问题，对于一个点 \((i,pre_i)\) 的贡献为 \(i-pre_i\)，每次询问就是求以 \((l,l)\) 为左下角，\((r,r)\) 为右上角这个矩形内所有点的贡献。

在线可以用分块/树套树来维护。

离线可以用莫队/ cdq 来维护。

CF364D Ghd

*2900

tag：随机化，暴力枚举

题目描述

给定一个大小为 \(n(1\le n\le 10^6)\) 的可重集 \({a_1,a_2,\dots,a_n}(1\le a_i\le 10^12)\)，求出这个集合所有大小大于 \(\frac{n}{2}\) 的子集的 gcd 的最大值。

思路

若我们确定了一个数 \(a_p\) 它一定存在于最后的答案当中，那么答案一定是 \(a_p\) 的某个因子。

通过枚举 \(a_p\) 的每一个因子可以暴力的求出存在 \(a_p\) 时的答案，时间复杂度为 \(O(d(a_p)^2)\)，一共需要做 \(n\) 次。

这肯定不能接受。但是题目满足至少有 \(\frac{n}{2}\) 个数一定存在于答案当中，也就是说，我们随机选取一个数在答案当中的概率为 \(\frac{1}{2}\)。

所以，我们只需要随机选取 \(k\) 次 \(p\) 即可求出答案，正确的概率为 \(1-\frac{1}{2}^k\)，时间复杂度 \(O(kd(a_p)^2)\)，实际上 \(d(x)\) 是 \(O(x^{\frac{1}{3}})\) 的量级的，随机 \(k=10\) 次即可通过。

CF1334F Strange Function

*2500

tag：动态规划 dp，数据结构

题目描述

定义函数 \(f\)：\(f(x)\) 为所有满足 \(x_i>x_{1,2,\cdots,i-1}\) 的 \(x_i\) 组成的序列。

给出两个序列 \(a,b\)，你可以删掉 \(a\) 中的一些元素。删掉 \(a_i\) 的代价为 \(p_i\)。你需要求出最小代价使得 \(f(a)=b\) 或给出无解。

数据范围：\(1\le n\le 5\times 10^5\)。

思路

将问题转化为保留一些元素，使得保留的元素代价和最大。

考虑 dp，定义 \(f_{i,j}\) 表示用 \(A\) 的前 \(i\) 个数匹配了 \(b_j\) 的最大代价和。

分以下三种情况来讨论：

• \(A_i>B_j\)，此时选择 \(A_i\)，必然会使 \(f(A)\) 中存在 \(A_i\)，而 \(A_i\) 和 \(B_j\) 有不匹配，所以 \(A_i\) 不能选。

• \(A_i=B_j\)，此时可以选择 \(A_i\)，并决定 \(A_i\) 是否匹配 \(B_j\)，所以有转移 \(f_{i,j}=\max\{f_{k,j}+\max(0,p_i),f_{k,j-1}+p_i\}(0\le k< i)\)。

• \(A_i=B_j\)，此时无论是否选择 \(A_i\)，\(f(A)\) 中都不可能存在 \(A_i\)，所以有 \(f_{i,j}=\max\{f_{k,j}+\max(0,p_i)\}(0\le k< i)\)。

直接转移是 \(O(n^2m)\) 的，可以过维护每个 \(j\) 的前缀最大值优化到 \(O(nm)\)。

之后可以用数据结构维护后缀加，单点最大值，来优化到 \(O(n\log m)\)。

CF1773I Interactive Factorial Guessing

*2500

tag： 暴力枚举，交互题

题目描述

你需要找到一个数 \(n(1\le n\le 5982)\)，你可以进行至多 \(10\) 次询问，每次询问可以询问 \(n!\) 的第 \(x\) 位上的值。

思路

通过一个位置的值，我们可以将这些数分成至多 \(10\) 个部分。

同时 \(n\) 有很小，于是我们考虑将每个 \(n\) 的阶乘预处理出来，每次询问可以选取出现数字最多的最小的那一位来询问，可以在 \(10\) 次以内得出答案。

注意一些实现上的细节：第一次询问的位置是固定的；只需要询问前 \(2000\) 位就可以得出答案。

CF351C Jeff and Brackets

*2500

tag：动态规划，矩阵快速幂优化 dp

题目描述

构造一个长度为 \(n\times m\) 的合法括号序列，在第 \(i\) 个位置上放左括号的代价为 \(a_{i\bmod n}\)，右括号代价为 \(b_{i\bmod n}\)，最小化构造的括号序列的代价。

数据范围：\(1\le n\le \color{red}{10^5}\color{black},1\le m\le 10^7\)。

思路

先考虑一个朴素的 dp：定义 \(f_{i,j}\) 表示当前在第 \(i\) 个位置，还剩余了 \(j\) 个左括号的最小代价。

有转移：

\[f_{i,j}=\begin{cases} \min\{f_{i-1,j-1}+a_{i\bmod n},f_{i-1,j+1}+b_{i\bmod n}\} & j>0\\ f_{i-1,j+1}+b_{i\bmod n} & j=0 \end{cases} \]

直接转移是 \(O(n^2m^2)\) 的。

相当于有 \(m\) 段，每一段的转移是相同的，只要知道上一段剩下来几个左括号就可以将一段整体的转移。

实际上，\(j\) 最大只有 \(n\)。

可以用矩阵快速幂来维护转移。

时间复杂度 \(O(n^3\log m)\)。

CF351C Jeff and Brackets 改

数据范围改为：\(1\le n\le \color{red}{10^5}\color{black},1\le m\le 10^9\)。

需要一种 \(O(n\log n)\) 的做法。

CF1380F Strange Addition

*2600

tag：矩阵，数据结构，动态 dp / ddp

题目描述

对于非负整数 \(a,b\)，定义它们的 "奇异加法 \(\oplus\)" 如下：

1. 将 \(a,b\) 一上一下写在两行，并按照低位对齐。
2. 将它们的每一位加起来，并将每一位的结果从高位到低位连接在一起，得到的就是 \(a\oplus b\)。

（你可以认为，两个数都有无穷多的前导 0）

你现在有一个仅包含 \(n\) 个 \(0\sim 9\) 的数码的字符串 \(c\)，并且还有 \(m\) 次操作。一次操作为：

• x d - 将 \(c\) 的第 \(x\) 个数码替换成数码 \(d\) 。

（注意，\(c\) 在任何时刻都可能存在前导 0）

每次操作过后，你需要输出，有多少个有序对 \((a,b)\)，满足 \(a,b\) 都是非负整数，且 \(a\oplus b=c\)。

思路

进位只会在前一位是 \(1\) 的情况下发生。

可以写出一个 dp，令 \(f_i\) 表示当前处理到 \(c\) 的前 \(i\) 个数的方案数。

有转移：\(f_{i}=(c_i+1)\times f_{i-1}+[c_{i-1}=1]\cdot(9-c_i)\times f_{i-2}\)。

然后有 \(m\) 次修改。

将转移写成矩阵形式：

\[(f_i,f_{i-1})=(f_{i-1},f_{i-2})\times \begin{pmatrix} c_i+1,&1\\ [c_{i-1}=1](9-c_i),&0 \end{pmatrix} \]

直接用线段树维护。

初值 \(f_{0}=f_{-1}=1\)。

注意修改时要修改 \(x\) 和 \(x+1\)。

时间复杂度 \(O(n\log n)\)。

CF1957F Frequency Mismatch

*2600/2700

tag：随机赋权，主席树，二分

题目描述

给定有 \(n(1\le n\le 10^5)\) 个节点的一棵树，树上的每个节点有一个颜色。

有 \(q\) 次询问，每次询问给出 \(u_1,v_1,u_2,v_2,k(1\le k\le 10)\)，求出 \(k\) 中颜色，满足该颜色在从 \(u_1\) 到 \(v_1\) 的路径上出现的次数与从 \(u_2\) 到 \(v_2\) 的次数不同。

思路

考虑随机赋权。

那么对于一个值域区间若此区间内所有颜色的和不同，那么就存在一种颜色满足条件。

可以用主席树储存信息，每次二分来找满足条件的颜色，找到 \(k\) 个后直接退出。

CF138D World of Darkraft

*2500

tag：博弈论，动态规划 dp

题目描述

有一个 \(n\times m(1\le n,m\le 20)\) 的棋盘，每个格子上有一个字母，初始时棋盘全部为白色。现在有两个人要轮流在棋盘上对决。每次会选择一个白色的格子，然后：

• 若该格子上的字母为 L，则将直到该格子左下或右上的第一个黑色格子（或边界）的格子全部涂黑。
• 为 R，方向为左上或右下。
• 为 X，相当于同时有 L 和 R。

最后无法选择格子的人输，判断先手是否有必胜策略。

思路

将棋盘转 45 度，将 \((i,j)\) 对应到 \((i+j,i-j+m)\) 上。

每次选择相当于横着或竖着将这个联通块切成两部分。

可以用四个字母 \(x,y,X,Y\) 来代表从 \((x,y)\) 到 \((X,Y)\) 这个联通块。

连通块内的切割不会影响到其它连通块。

所以我们每次切完后可以将两个连通块分开考虑。

用 sg 函数来计算答案。

枚举当前连通块内的每一个方格 \((dx,dy)\)，

• 若该方格为 L，那么有 \(sg(x,dx-1,y,Y)\oplus sg(dx+1,X,y,Y)\) 的贡献。
• 其它两种情况同理。

可以将原图黑白染色，然后单独考虑黑点和白点，他们是不影响的。