2024/9/26

今天上午是 spdarkle 的 Solution Set 分享，成功荒废一上午。

题还没做完，先写一些。

CF1909F1 Small Permutation Problem (easy verson)

先考虑 F1 即不存在 \(a_i=-1\) 的情况。

我们将这个问题看出在棋盘上的问题，对于第 \(i\) 个 \(a_i\) 的限制就相当于限制了左下角 \(i\times i\) 的矩形内必须恰好放置 \(a_i\) 个棋子。

那么 \(a_i\) 相较于 \(a_{i-1}\) 就相当于多出了一块 L 型的区域，而我们需要在这个区域内放上 \(a_i-a_{i-1}\) 个棋子。

首先，因为给定的 \(p_i\) 是一个排列，所以每个棋子的横坐标都是互不相同的，而我们放上的棋子也需要保证纵坐标互不相同。

那么，在这个 L 型的区域内，我们至多只能放 \(2\) 个棋子，所以当 \(a_i-a_{i-1}>2\) 时是无解的。

所以，让我们按照相邻两个 \(a_i\) 的差值 \(d\) 来进行分类讨论：

• 若 \(d=0\)，则我们不需要再放上棋子，直接 \(f_i=f_{i-1}\)。
• 若 \(d=1\)，则我们需要放上一个棋子，于是有 \(f_i=f_{i-1}+2(i-a_{i-1})-1\)，这是因为我们在 \(i-1\) 的 L 型区域内已经放入了 \(a_{i-1}\) 个棋子，并且每一个棋子均会使得一行和一列上无法放置棋子。
• 若 \(d=2\)，则我们需要放上两个棋子，于是有 \(f_{i}=f_{i-1}+(i-a_{i-1}-1)^2\)，这时右上角的一个格子是不能填的，所以只有 \(i-a_{i-1}-1\) 种方式。

可以在 \(O(n)\) 的复杂度内解决这个问题。

CF1909F2 Small Permutation Problem (hard verson)

然后让我们来考虑 F2。

F2 相较于 F1 的区别在于多了 \(-1\)，这会导致 L 型区域变大，F1 的分类讨论就无法继续使用了。

现在，这个 L 型区域的边长变为了 \(a_i\) 到上一个不是 \(-1\) 的 \(a_j\) 的距离，记为 \(d\)。

我们将这个 L 型分成两部分，如下图：

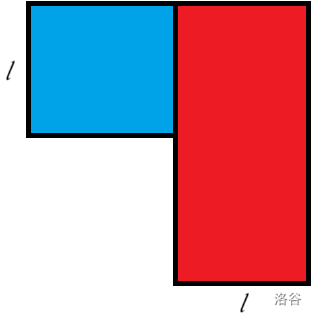
先让我们排除掉已经不能够选择的部分。

不妨让我们来枚举左边蓝色部分放置的棋子数 \(k\)。并且蓝色部分每放置一个棋子会导致红色部分少一个可用行。

蓝色矩形的长宽分别为 \(i-j\) 和 \(j-a_j\)，红色矩形的长宽分别为 \(i-j\) 和 \(i-a_j\)，若蓝色部分放置了 \(k\) 个棋子，可以得到：

\[(C_{i-j}^kC_{j-a_j}^kk!)\times(C_{i-j}^{d-k}C_{i-a_j-k}^{d-k}(d-k)!) \]

答案是每一段的答案的乘积。时间复杂度为每一段长度的和，也就是 \(\sum d=O(n)\)。

CF1863G Swaps

我们按照 \(i\) 向 \(a_i\) 连边，最后可以得到一个基环树森林，我们将每棵基环树单独考虑。

考虑一次 swap 操作对图结构的影响。可以发现，每次 swap 操作相当于将一个点 \(u\) 连向它父亲的父亲，并将 \(u\) 的父亲变成自环。

也就是说，若现在有 \(a\to b\to c\)，若我们 swap(a,b)，那么会变成 \(a\to c\) 和 \(b\to b\)。

让我们再考虑，若一个点 \(b\) 有自环，若有边 swap(a,b)，那么仍然是 \(a\to b\)，也就是说，每个点会被直接于它有边相连的点操作一次。

于是我们记第 \(i\) 个点的入度为 \(in_i\)，我们有 \(\prod(in_i+1)\)，这样子算是不会漏的，因为一棵树会对于一个唯一的排列 \(p\)。

但这在环上时不适用的，因为我们无法通过一些操作使得环上的每一条边都被操作，当最后还剩下一条边时环上所有点都已经全是自环了。

同时我们发现，对于所有只剩下一条边的方案，所得到的排列都是相同的，所以我们还需要减去 \(\sum in_{c_i}\)。

CF1750F Majority

不妨让我们来考虑什么序列是不合法的：若我们可以将原序列划分为 \(2k+1\) 个段，且每一个偶数段的长度大于左右两奇数段的长度。

于是我们设 \(f_{i,j}\) 表示当前序列长度为 \(i\)，最后一段的长度为 \(j\) 的方案数。