互信息

参考
互信息是信息论中用以评价两个随机变量之间的依赖程度的一个度量。
相关概念：

• 信息量：是对某个事件发生或者变量出现的概率的度量，一个事件发生的概率越低，这个事件包含的信息量越大，这跟我们直观上的认知也是吻合的，越稀奇新闻包含的信息量越大，因为这种新闻出现的概率低。香农提出了一个定量衡量信息量的公式：$log \frac{1}{p}=-log p$
• 熵(entropy)：是衡量一个系统的稳定程度。其实就是一个系统所有变量信息量的期望或者说均值。
  $$H(X)=\sum_{x\in X}P(x)log \frac{1}{P(x)}=-\sum_{x \in X}P(x)log P(x)=-E log \ P(x)$$

当一个系统越不稳定，或者事件发生的不确定性越高，它的熵就越高。
以投硬币为例，正面的概率为​, 反面的概率则为​,那么这个系统的熵就是​
显然易得，当​时，​的取值最大，也就印证了 事件发生的不确定性越高，它的熵就越高。

• 联合熵：多个联合变量的熵，也就是多个变量联合的熵
  $$H(X,Y)=\sum_{x\in X}\sum_{y\in Y}P(x,y\log\frac{1}{P(x,y)})=-E\log P(X,Y)$$

• 条件熵：一个随机变量在给定的情况下，系统的熵。

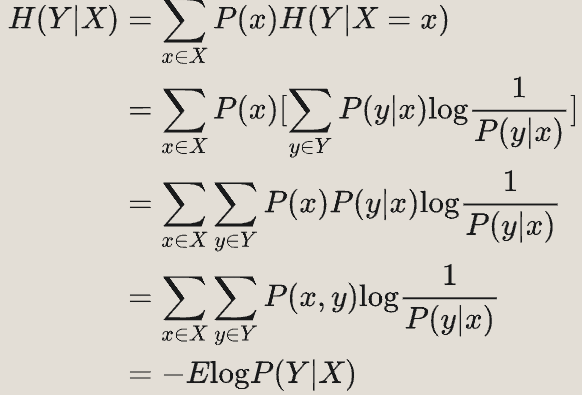
• 互信息：如下图，互信息就是​，即​与​交叉的部分。其等价于
  $I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)$

区别:
互信息描述的是同一个系统下两个子系统的对应部分的信息量；
信息增益描述的是同一个系统下，不同状态的信息量。

• 交叉熵描述的是两个概率分布之间的差异，用于评估模型的性能。
• KL散度是衡量一个概率分布P相对于另一个概率分布Q的差异，用于评估模型预测的不确定性。
• 互信息是衡量两个随机变量之间的信息共享量，用于特征选择和提取。