时间复杂度与空间复杂度-(小灰和大黄)
2020年12月5日
01 时间复杂度
怎样来衡量算法的好坏?
衡量算法的好坏有很多标准,其中最重要的两大标准是算法的时间复杂度和空间复杂度。
时间复杂度和空间复杂度究竟是什么呢?首先,让我们来想象一个场景。
某一天,小灰和大黄实现同一个需求。一天后,小灰和大黄交付了各自的代码,两人的代码实现的功能差不多。
大黄的代码运行一次要花100ms,占用内存5MB。
小灰的代码运行一次要花100s,占用内存500MB。
在上述场景中,小灰虽然也按照老板的要求实现了功能,但他的代码存在两个很严重的问题。
- 运行时间长
- 占用空间大
由此可见,运行时间的长短和占用内存空间的大小,是衡量程序好坏的重要因素。
可是,如果代码都还没有运行,我怎么能预知代码运行所花的时间呢?
由于受运行环境和输入规模的影响,代码的绝对执行时间是无法预估的。但我们却可以预估代码的基本操作执行次数。
1.1) 基本操作执行次数
关于代码的基本操作执行次数,下面用生活中的4个场景来进行说明。
eg-(1a)------------------
场景1:给小灰1个长度为10cm的面包,小灰每3分钟吃掉1cm,那么吃掉整个面包需要多久?
🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖🥖
答案自然是3×10即30分钟。
如果面包的长度是n厘米呢?
此时吃掉整个面包,需要3乘以n即3n分钟。
如果用一个函数来表达吃掉整个面包所需要的时间,可以记作\(T(n)=3n\),\(n\)为面包的长度。
eg-(2a)------------------
场景2:给小灰1个长度为16cm的面包,小灰每5分钟吃掉面包剩余长度的一半,即第5分钟吃掉8cm,第10分钟吃掉4cm,第15分钟吃掉2cm……那么小灰把面包吃得只剩1cm,需要多久呢?
这个问题用数学方式表达就是,数字16不断地除以2,那么除几次以后的结果等于1?这里涉及数学中的对数,即以2为底16的对数\(log16\)。
因此,把面包吃得只剩下1cm,需要\(5×log16\)即20分钟。
如果面包的长度是n厘米呢?
此时,需要5乘以\(logn\)即\(5logn\)分钟,记作\(T(n)=5logn\)。
eg-(3a)------------------
场景3:给小灰1个长度为10cm的面包和1个鸡腿,小灰每2分钟吃掉1个鸡腿。那么小灰吃掉整个鸡腿需要多久呢?
🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗🍗
答案自然是2分钟。因为这里只要求吃掉鸡腿,和10cm的面包没有关系。
如果面包的长度是n厘米呢?
无论面包多长,吃掉鸡腿的时间都是2分钟,记作\(T(n)=2\)。
eg-(4a)------------------
场景4:给小灰1个长度为10cm的面包,小灰吃掉第1个1cm需要1分钟时间,吃掉第2个1cm需要2分钟时间,吃掉第3个1cm需要3分钟时间……每吃1cm所花的时间就比吃上一个1cm多用1分钟。那么小灰吃掉整个面包需要多久呢?
答案是从1累加到10的总和,也就是55分钟。
如果面包的长度是n厘米呢?
根据高斯算法,此时吃掉整个面包需要\(1+2+3+…+(n-1)+n\),即\((1+n)×n/2\)分钟,也就是\(0.5n^2+0.5n\)分钟,记作\(T(n)=0.5n^2 + 0.5n\)。
上面所讲的是吃东西所花费的时间,这一思想同样适用于对程序基本操作执行次数的统计。设\(T(n)\)为程序基本操作执行次数的函数(也可以认为是程序的相对执行时间函数),n为输入规模,刚才的4个场景分别对应了程序中最常见的4种执行方式。
eg-(1b)------------------
场景1:\(T(n)=3n\),执行次数是线性的。
void eat1(int n) {
for(int i = 0; i < n; i++) {;
System.out.println("等待1分钟");
System.out.println("等待1分钟");
System.out.println("吃1cm面包");
}
}
eg-(2b)------------------
场景2:\(T(n) = 5logn\),执行次数是用对数计算的
void eat2(int n) {
for(int i = n; i > 1; i /= 2) {
System.out.println("等待1分钟");
System.out.println("等待1分钟");
System.out.println("等待1分钟");
System.out.println("等待1分钟");
System.out.println("吃一半面包");
}
}
eg-(3b)------------------
场景3:\(T(n) = 2\),执行次数是常量。
void eat3(int n) {
System.out.println("等待1分钟");
System.out.println("吃1个鸡腿");
}
eg-(4b)------------------
场景4:\(T(n) = 0.5n^2 + 0.5n\),执行次数是用多项式计算的。
void eat4(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < i; j++) {
System.out.println("等待1分钟");
}
System.out.println("吃1cm面包");
}
}
1.2) 渐进时间复杂度
有了基本操作执行次数的函数\(T(n)\),是否就可以分析和比较代码的运行时间了呢?还是有一定困难的。
例如算法A的执行次数是\(T(n)=100n\),算法B的执行次数是\(T(n)=5n^2\),这两个到底谁的运行时间更长一些呢?这就要看\(n\)的取值了。
因此,为了解决时间分析的难题,有了渐进时间复杂度(asymptotic time complexity)的概念,其官方定义如下。
def-若存在函数\(f(n)\),使得当\(n\)趋近于无穷大时,\(T(n)/f(n)\)的极限值为不等于零的常数,则称\(f(n)\)是\(T(n)\)的同数量级函数。记作\(T(n)=O(f(n))\),称为\(O(f(n))\),\(O\)为算法的渐进时间复杂度,简称为时间复杂度。
直白地讲,时间复杂度就是把程序的相对执行时间函数\(T(n)\)简化为一个数量级,这个数量级可以是\(n\)、\(n^2\)、\(n^3\)等。
如何推导出时间复杂度呢?有如下几个原则。
- 如果运行时间是常数量级,则用常数1表示
- 只保留时间函数中的最高阶项
- 如果最高阶项存在,则省去最高阶项前面的系数
让我们回头看看刚才的4个场景。
eg-(1c)------------------
场景1:\(T(n) = 3n\)
最高阶项为\(3n\),省去系数3,则转化的时间复杂度为:\(T(n) = O(n)\)。
eg-(2c)------------------
场景2:\(T(n) = 5logn\)
最高阶项为\(5logn\),省去系数5,则转化的时间复杂度为:\(T(n) = O(logn)\)。
eg-(3c)------------------
场景3:\(T(n) = 2\),只有常数量级,则转化的时间复杂度为:\(T(n) = O(1)\)。
eg-(4c)------------------
场景4:\(T(n) = 0.5n^2 + 0.5n\)
最高阶项为\(0.5n^2\),省去系数0.5,则转化的时间复杂度为:\(T(n)=O(n^2)\)。
这4种时间复杂度究竟谁的程度执行用时更长,谁更节省时间呢?
当n的取值足够大时,不难得出下面的结论:
\(O(1) < O(logn) < O(n) < O(n^2)\)
在编程的世界中有各种各样的算法,除了上述4个场景,还有许多不同形式的时间复杂度,例如:
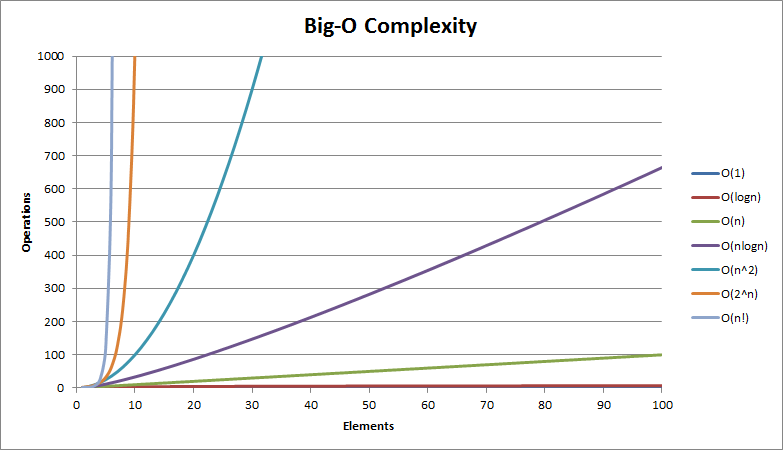
\(O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^k) < O(2^n) < O(a^n) < O(n!)\)
02 空间复杂度
在运行一段程序时,我们不仅要执行各种运算指令,同时也会根据需要,存储一些临时的中间数据,以便后续指令可以更方便地继续执行。
在什么情况下需要这些中间数据呢?让我们来看看下面的例子。
给出下图所示的n个整数,其中有两个整数是重复的,要求找出这两个重复的整数。

对于这个简单的需求,可以用很多种思路来解决,其中最朴素的方法就是双重循环,具体如下。
遍历整个数列,每遍历到一个新的整数就开始回顾之前遍历过的所有整数,看看这些整数里有没有与之数值相同的。
第1步,遍历整数3,前面没有数字,所以无须回顾比较。
第2步,遍历整数1,回顾前面的数字3,没有发现重复数字。
第3步,遍历整数2,回顾前面的数字3、1,没有发现重复数字。

后续步骤类似,一直遍历到最后的整数2,发现和前面的整数2重复。

双重循环虽然可以得到最终结果,但它显然并不是一个好的算法。它的时间复杂度是多少呢?
根据上一节所学的方法,我们不难得出结论,这个算法的时间复杂度是\(O(n^2)\)。
那么,怎样才能提高算法的效率呢?在这种情况下,我们就有必要利用一些中间数据了。
如何利用中间数据呢?
当遍历整个数列时,每遍历一个整数,就把该整数存储起来,就像放到字典中一样。当遍历下一个整数时,不必再慢慢向前回溯比较,而直接去“字典”中查找,看看有没有对应的整数即可。
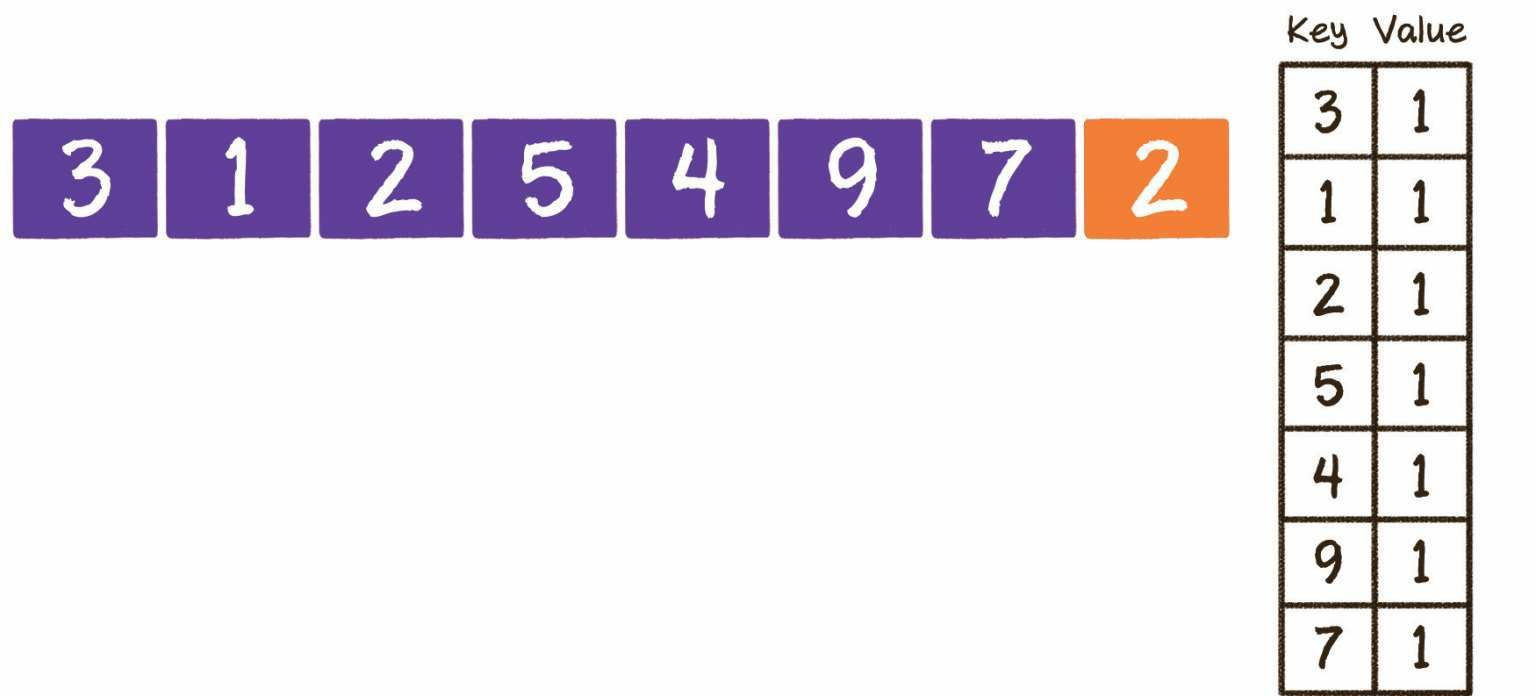
“字典”左侧的Key代表整数的值,“字典”右侧的Value代表该整数出现的次数(也可以只记录Key)。
接下来,当遍历到最后一个整数2时,从“字典”中可以轻松找到2曾经出现过,问题也就迎刃而解了。
由于读写“字典”本身的时间复杂度是\(O(1)\),所以整个算法的时间复杂度是\(O(n)\),和最初的双重循环相比,运行效率大大提高了。
而这个所谓的“字典”,是一种特殊的数据结构,叫作散列表。这个数据结构需要开辟一定的内存空间来存储有用的数据信息。
但是,内存空间是有限的,在时间复杂度相同的情况下,算法占用的内存空间自然是越小越好。如何描述一个算法占用的内存空间的大小呢?这就用到了算法的另一个重要指标——空间复杂度(space complexity)。
和时间复杂度类似,空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,它同样使用了大O表示法。
程序占用空间大小的计算公式记作\(S(n)=O(f(n))\),其中\(n\)为问题的规模,\(f(n)\)为算法所占存储空间的函数。
2.1) 空间复杂度的计算
常见的空间复杂度有下面几种情形。
- 常量空间
当算法的存储空间大小固定,和输入规模没有直接的关系时,空间复杂度记作\(O(1)\)。例如下面这段程序:
void fun1() {
int var = 3;
...
}
- 线性空间
当算法分配的空间是一个线性的集合(如数组),并且集合大小和输入规模\(n\)成正比时,空间复杂度记作\(O(n)\)。
例如下面这段程序:
void fun2(int n) {
int[] array = new int[n];
...
}
- 二维空间
当算法分配的空间是一个二维数组集合,并且集合的长度和宽度都与输入规模\(n\)成正比时,空间复杂度记作\(O(n^2)\)。
例如下面这段程序:
void fun3(int n) {
int[][] matrix = new int[n][n];
...
}
- 递归空间
递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或集合,但是计算机在执行程序时,会专门分配一块内存,用来存储“方法调用栈”。
“方法调用栈”包括进栈和出栈两个行为。
当进入一个新方法时,执行入栈操作,把调用的方法和参数信息压入栈中。
当方法返回时,执行出栈操作,把调用的方法和参数信息从栈中弹出。
下面这段程序是一个标准的递归程序:
void fun4(int n) {
if (n <= 1) {
return;
}
fun4(n-1);
...
}
假如初始传入参数值n=5,那么方法fun4(参数n=5)的调用信息先入栈。
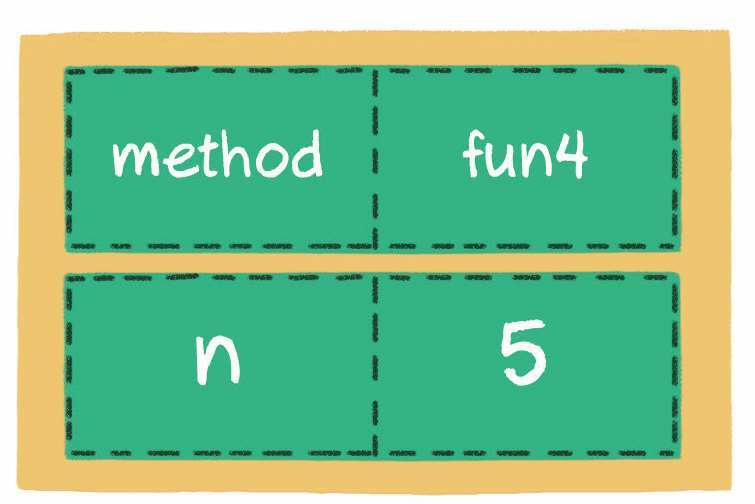
接下来递归调用相同的方法,方法fun4(参数n=4)的调用信息入栈。
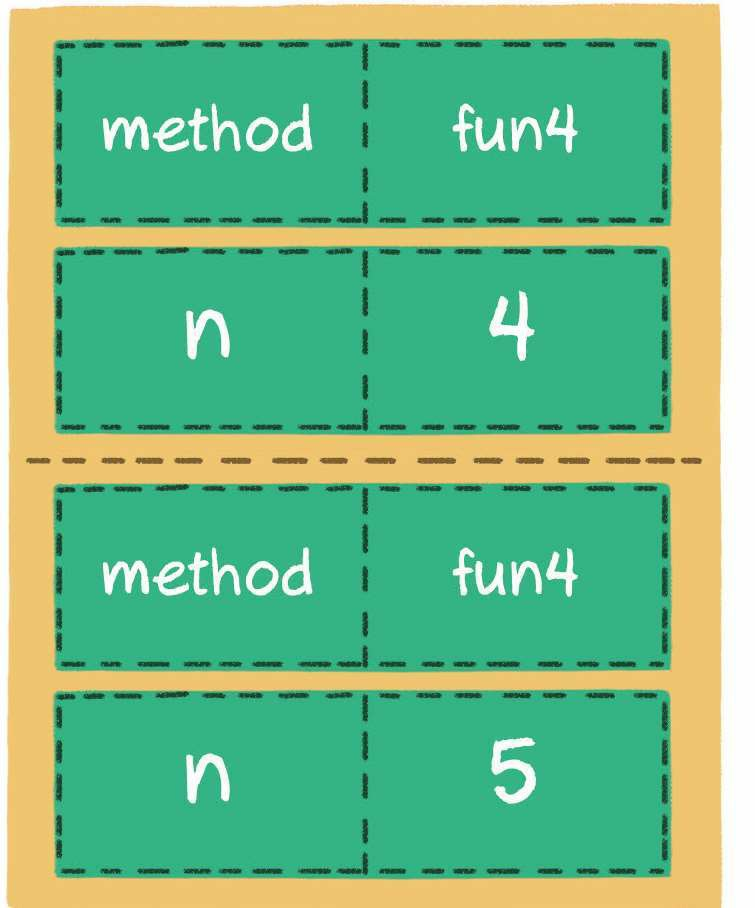
以此类推,递归越来越深,入栈的元素就越来越多。

当n=1时,达到递归结束条件,执行return指令,方法出栈。
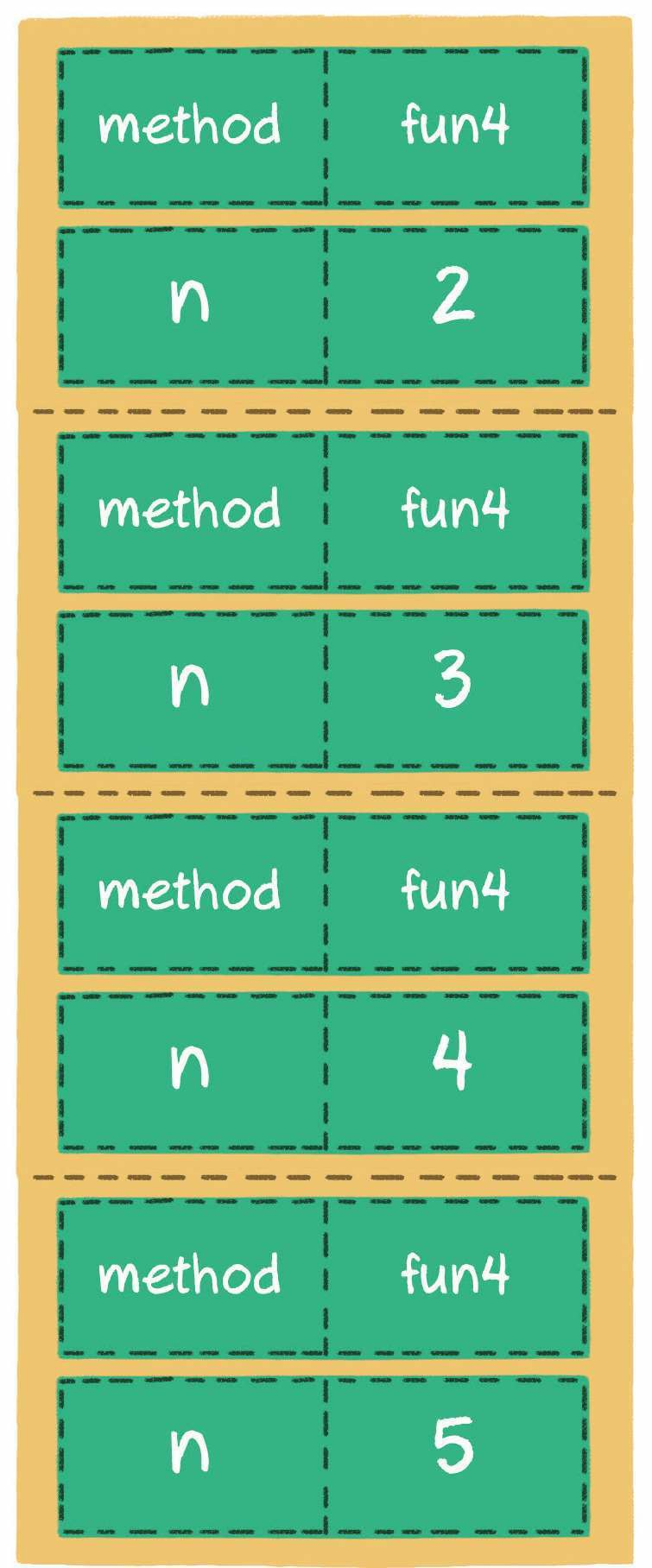
最终,“方法调用栈”的全部元素会一一出栈。
由上面“方法调用栈”的出入栈过程可以看出,执行递归操作所需要的内存空间和递归的深度成正比。纯粹的递归操作的空间复杂度也是线性的,如果递归的深度是n,那么空间复杂度就是O(n)。
03 时间与空间的取舍
人们之所以花大力气去评估算法的时间复杂度和空间复杂度,其根本原因是计算机的运算速度和空间资源是有限的。
就如一个大财主,基本不必为日常花销伤脑筋;而一个没多少积蓄的普通人,则不得不为日常花销精打细算。
对于计算机系统来说也是如此。虽然目前计算机的CPU处理速度不断飙升,内存和硬盘空间也越来越大,但是面对庞大而复杂的数据和业务,我们仍然要精打细算,选择最有效的利用方式。
但是,正所谓鱼和熊掌不可兼得。很多时候,我们不得不在时间复杂度和空间复杂度之间进行取舍。
在寻找重复整数的例子中,双重循环的时间复杂度是\(O(n^2)\),空间复杂度是\(O(1)\),这属于牺牲时间来换取空间的情况。
相反,字典法的空间复杂度是\(O(n)\),时间复杂度是\(O(n)\),这属于牺牲空间来换取时间的情况。
在绝大多数时候,时间复杂度更为重要一些,我们宁可多分配一些内存空间,也要提升程序的执行速度。
note:------------------------
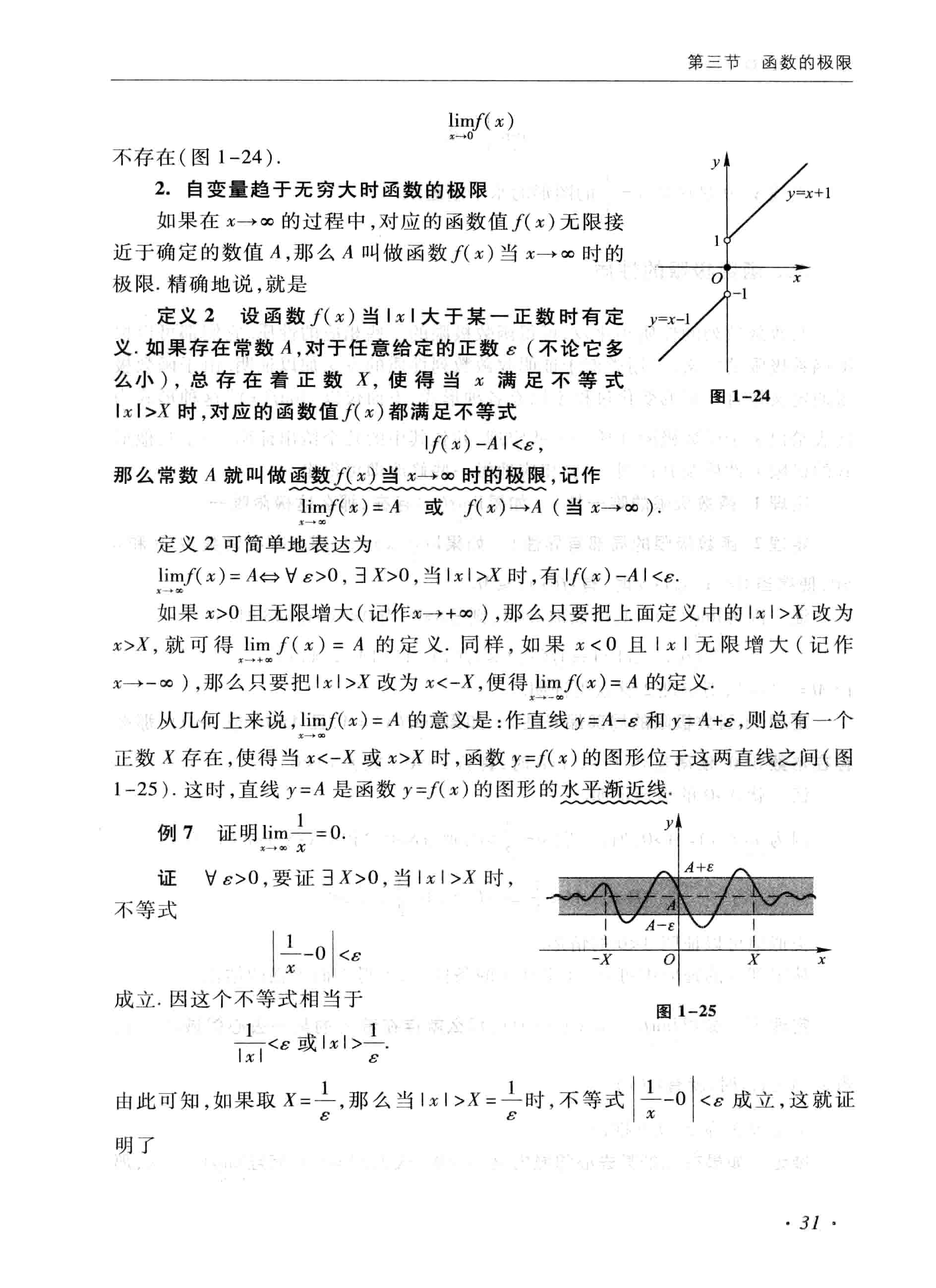
x趋于无穷大时函数的极限


 浙公网安备 33010602011771号
浙公网安备 33010602011771号