素数
一、定义
素数又称质数,是指一个大于1的正整数,除了1和它本身外,没有其他约数的自然数,否则称为合数(规定1既不是质数也不是合数)。
二、性质
质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,N+1是素数或者不是素数。






五、素数的判定
// 100 prime number // 筛选法 即:“埃拉托色尼筛选法” // 找出一个非素数就把它挖掉,最后剩下就是素数 /* * 找出1~n的素数表 * 1、挖去1 * 2、用下一个未挖去的数p去除p后面各数,把p的倍数挖掉 * 3、检查p是否小于n的整数部分(如果n=1000,则坚持p<31?), * 如果是,则返回(2)继续执行,否则结束。 * 4、剩下的就是素数了 */ #include<iostream> #include<iomanip> #include<cmath> using namespace std; int main() { int i, j, n, a[101]; for (i = 1; i <= 100; i++) { a[i] = i; } a[1] = 0; for (i = 2; i < sqrt(100); i++) { for (j = i + 1; j <= 100; j++) { if (a[i] != 0 && a[j] != 0) { if (a[j] % a[i] == 0) { a[j] = 0; } } } } cout<<endl; for (i = 1, n = 0; i <= 100; i++) { if (a[i] != 0){ cout<<setw(5)<<a[i]<<" "; n++; } if (n == 10) { cout<<endl; n = 0; } } cout<<endl; return 0;}线性是指O(n)内筛掉所有合数,还有一种方法叫埃氏筛法,我先证明埃氏筛法效率低,也就是会有重复。
证明如下:
埃氏筛法的原理是找到一个素数后,它的1~n倍就会被筛掉,任何一个合数都可以被拆成一个质数*另一个数的形式,我们对每一个质数对应的可能的(合)数都枚举了,这就保证了所有可能的合数都被筛掉了。为什么不是最优呢?问题出在那个质数上,对于一个合数m,m=h*P,P是质数且P>m的最小质因数,那么m也可以表示为m=H*p,(H是个比h大的合数,p是m的最小质因数),这样我们在枚举p的倍数时,m就被筛掉了,而在枚举P的倍数时,m又被筛掉了一次,造成效率浪费。
怎办呢?--------线性筛法
我们在枚举倍数时,保证当前质数不能整除这个倍数就好了,当然了,在之前要先筛一次,也就是p是m的p,这样我们在最优性的条件下,对每一个质数,它所有对应的倍数,都被枚举到,也就保证了可行性。
#include<bits/stdc++.h> using namespace std;
int n,cnt;
int prime[100000];
bool vis[100000];
void Euler(){
for(int i=2;i<=n;i++){
if(!vis[i]) prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
}
int main(){
cin>>n;
Euler();
for(int i=1;i<=cnt;i++)
cout<<prime[i]<<' ';
return 0;
}
(1)欧拉函数有以下五条性质:





由此,我们可以在素数线性筛的基础上筛出欧拉函数!
每次想要得到phi[n],详细过程如下:
若n为素数,根据①,有phi[n]==n-1
若a*b==n(a,b为任意互质数),根据②,有phi[n]==phi[a]*phi[b],这里的phi[a]和phi[b]都是已经得到的
若a*p==n(p为质数,且p是a的因数),根据⑤得phi[n]==phi[a]*p
代码如下:
C++:
1 #include<bits/stdc++.h>
2
3 using namespace std;
4
5 int const MAXN=100010;
6
7 int prime[MAXN],tot;
8 bool notprime[MAXN];
9 int euler[MAXN];
10
11 void pony_getPhi(int n){
12 notprime[0]=1;
13 notprime[1]=1;
14 euler[1]=1;
15 for(int i=2;i<=n;++i){
16 if(!notprime[i])
17 {
18 prime[tot++]=i;
19 euler[i]=i-1;//HERE 1
20 }
21 for(int j=0; j<tot && i*prime[j]<=n;++j){
22 notprime[i*prime[j]]=1;
23 if(i%prime[j]==0){euler[i*prime[j]]=euler[i]*prime[j];break;}//HERE 5
24 else euler[i*prime[j]]=euler[i]*euler[prime[j]];//HERE 2
25 }
26 }
27 }
28
29 int main(int argc,char *argv[],char *enc[]){
30 int m=100;
31 pony_getPhi(m);
32 for(int i=1;i<=m;++i){
33 printf("phi(%d):%d",i,euler[i]);
34 if(notprime[i]) printf("\n");
35 else printf(" [%d]Prime\n",i);
36 }
37 return 0;
38 }
5.莫比乌斯函数的线性筛法
莫比乌斯函数μ(d)的定义如下:
(1)若d=1,那么μ(d)=1
(2)若d=p1p2…pk(p1…pk均为互异质数),那么μ(d)=(−1)^k
(3)其他情况下,μ(d)=0
只要抓住定义就能轻松筛出莫比乌斯函数啦
代码如下:
#include<bits/stdc++.h>
using namespace std;
int const MAXN=100010;
int prime[MAXN],tot;
bool notprime[MAXN];
int miu[MAXN];
void pony_getMiu(int n){
notprime[0]=1;
notprime[1]=1;
miu[1]=1;//HERE 1
for(int i=2;i<=n;++i){
if(!notprime[i])
{
prime[tot++]=i;
miu[i]=-1;//HERE 2
}
for(int j=0; j<tot && i*prime[j]<=n;++j){
notprime[i*prime[j]]=1;
if(i%prime[j]==0){miu[i*prime[j]]=0;break;}//HERE 3
else miu[i*prime[j]]=-1*miu[i];//HERE 2
}
}
}
int main(int argc,char *argv[],char *enc[]){
int m=100;
pony_getMiu(m);
for(int i=1;i<=m;++i){
printf("miu(%d):%d",i,miu[i]);
if(notprime[i]) printf("\n");
else printf(" [%d]Prime\n",i);
}
return 0;
}
6.Miller-Rabin素数测试算法
(1)作用:
有时候我们想快速的知道一个数是不是素数,而这个数又特别的大导致 O( ) 的算法不能通过,这时候我们可以对其进行 Miller-Rabin 素数测试,可以大概率测出其是否为素数。
(2)两个基础理论
证明转载费马小定律&二次探测的证明
①费马小定理:当 为质数,有
,不过反过来不一定成立,也就是说,如果
,
互质,且
,不能推出
是质数,比如
数(这个就自行百度吧)
②二次探测:如果 是一个素数,
, 则方程
的解为
或
(3)算法流程

(4)备注
①我们可以多选择几个 a,如果全部通过,那么 x 大概率是质数。
②Miller-Rabin 素数测试中,“大概率”意味着概率非常大,基本上可以放心使用。
③当 a 取遍小等于 30 的所有素数时,可以证明 int 范围内的数不会出错。
④代码中我用的 int 类型,不过实际上 Miller-Rabin 素数测试可以承受更大的范围。
⑤另外,如果是求一个 long long 类型的平方,可能会爆掉,因此有时我们要用“快速积”,不能直接乘。


7.Pollard-Rho算法--大数分解

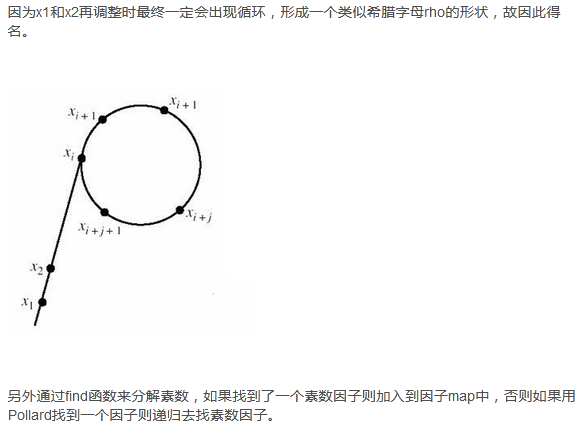



参考:(仅限内部使用)
1.百度百科;
2.https://blog.csdn.net/forever_dreams/article/details/82314237
3.https://blog.csdn.net/ECNU_LZJ/article/details/72675595/
4.转载于:https://www.cnblogs.com/fzl194/p/9047710.htm



 浙公网安备 33010602011771号
浙公网安备 33010602011771号