线性同余方程

一、定义

         1.不定方程：未知数的个数多于方程个数，且未知数受到某些限制（如要求是整数）的方程。

       2.同余方程：设函数 f(x)=a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀，则称：f(x)≡0(mod m)是关于模 m 的同余方程。

       3.线性：方程的未知数次数是一次。

        4.线性同余方程: 线性同余方程是最基本的同余方程，形如 ax≡b (mod m) 的未知数是 x 的同余式，其中a、b 是整数，且a≠0 (mod m)。

二、与线性同余方程有关的定理

       1.定理1：对于方程 a*x+b*y=c ，该方程等价于a*x≡c(mod b)，有整数解的充分必要条件：c%GCD（a,b）=0。

     根据定理1，对于a*x+b*y=c，我们可以先用扩展欧几里得算法求出一组x₀,y₀,也就是a*x₀+b*y₀=GCD(a,b),然后两边同时除以GCD（a,b),再乘c。这样就得到了方程a*x₀*c/GCD(a,b)+b*y₀*c/GCD(a,b）=c,我们也就找到了方程的一个解。

       2.定理2：若GCD(a,b)=1,且x₀,y₀为a*x+b*y=c 的一组解，则该方程的任一解可表示为：x=x₀+b*t,y=y₀-a*t,且对任一整数t,皆成立。

     根据定理2，可以求出方程的所有解。但实际问题中，我们往往被要求去求最小整数解，也就是求一个特解x，t=b/GCD(a,b),x=(x%t+t)%t。

       3.定理3：若 GCD(a,b)=d，则方程 a*x≡ c (mod b) 在 [0, b/d - 1] 上有唯一解。

三、线性同余方程的解的求法

         1.使用扩展欧几里德算法求方程的一组解

                根据定理1，对于方程a*x+b*y=c ，用扩展欧几里德算法求出一组x₀、y₀，即令a*x₀+b*y₀=GCD(a,b)，然后两边同除GCD(a,b) ，再乘以c ，即得方程 a*x₀*c/GCD(a,b)+b*y₀*c/GCD(a,b)=c ，因此可知方程的一组解。

         2.实际应用

                实际中，常常被要求去求最小的正整数的解，先通过扩展欧几里德算法求出方程的一组 x₀、y₀，再设 t=b/GCD(a,b) ，通过定理2来拓展方程的解，来调整x的范围，将 a*x₀+b*y₀=c 拓展为 a*(x₀+t*k)+b*(y₀-t*k)=c,k 为整数 ，从而使得所得到的x 尽可能的小，通过式子 x=(x mod t + t)mod t 来约束结果，一定是一个正数，最后所得到的x 即是一个最小的正整数解。

 

 

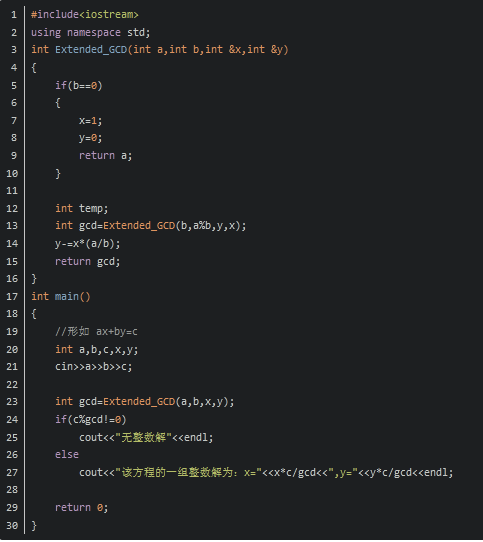
四、【例题】

• 青蛙的约会（POJ-1061）(扩展欧几里得)：点击这里
  同题：青蛙的约会（洛谷-P1516）：点击这里
• The Balance（POJ-2142）(线性同余方程)：点击这里
• C Looooops（POJ-2115）(线性同余方程)：点击这里
• 转载：https://blog.csdn.net/u011815404/article/details/81302830