Search Tree

大体内容整理自UCB-CS61B 教材的Lec16-18(因此采用java语言)
CS61B-Textbook

大致顺序是-BST-B树-红黑树-AVL

给大家推荐一个可视化数据结构的网站
Data Structure Visualizations

1. 二叉搜索树 BST(Binary Search Tree)

对于链表数据结构, 我们如果通过遍历数组来查找一个key所需要的时间都是 \(O(n)\), 很自然的我们会想到, 对有序数组使用二分查找的效率是 \(O(\log n)\).
为了实现高效的中间插入, 我们选择链表数据结构, 但是因为链表的索引访问.get(i)的效率是 \(O(n)\), 若对一有序链表采用二分访问, 其效率应为 \(O(n\cdot \log n)\), 甚至不如直接遍历搜索.
如何简化在链表中的高效二分查找呢? 我们考虑在有序的链表中储存其中间的值的索引, 即

Node mid = this.get(Math.floor(size / 2))

类似地, 我们通过与中间的值的比较, 又递归的获得了两个子链表, 我们继续储存其中间的值的索引

如此递归的操作, 我们事实上已经获得了一个二叉树结构储存的索引, 所以我们可以通过如上的过程, 通过二叉树储存一系列可比较的值, 从而得到二叉搜索树BST.

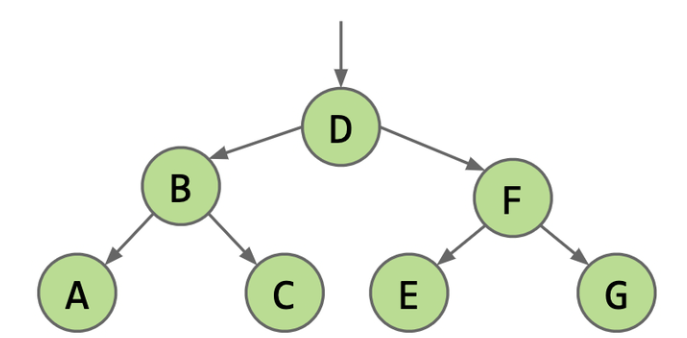
我们先给出几个严格的定义:

1.1 BST的相关定义

树是 \(n\) 个结点的有限集. 当 \(n=0\) 时, 称为空树. 在任意一棵树非空树中应满足:

有且仅有一个特定的称为根 (root) 的结点；
当 \(n>1\) 时, 其余结点可分为 \(m\) 个互不相交的有限集 \(T_1,T_2,...T_m\), 其中每一个集合本身又是一颗树, 并且称为根的子树(SubTree)

二叉树, 则是每个结点都只有两个子树的树, 被称为"左子树"和"右子树"(也即, 二叉树的左右子树是有次序的)特点包括：

每个结点最多有两个子结点, 分别称为左子结点和右子结点
左子树和右子树都是二叉树, 它们本身也可以是空树
二叉树的结点结构包含一个数据元素和指向左右子树的指针

以下是一些常见的术语:

结点: 包含一个数据元素及若干指向其子树的分支
结点的度: 一个结点拥有的子树的数目
叶子或终端结点: 度为 \(0\) 的结点
非终端结点或分支结点: 度不为 \(0\) 的结点
树的度: 树内各结点的度的最大值
孩子结点或子结点: 结点的子树的根称为该结点的孩子结点或子结点
双亲结点或父结点: 若一个结点含有子结点, 则这个结点称为其子结点的双亲结点或父结点
兄弟结点: 同一个双亲的孩子之间互称兄弟
祖先结点: 从根到该结点所经分支上的所有结点
子孙结点: 以某结点为根的子树中任一结点都称为该结点的子孙
结点的层次: 从根开始定义起, 根为第一层, 根的孩子为第二层. 若某结点在第 \(L\) 层, 则其子树的根就在第 \(L+1\) 层
堂兄弟结点: 其双亲在同一层的结点互为堂兄弟
树的深度或高度: 树中结点的最大层次
森林: 由 \(m(m\ge0)\) 棵互不相交的树的集合称为森林
有序树和无序树: 树中结点的各子树从左到右是有次序的, 不能互换, 称该树为有序树, 否则称为无序树
路径和路径长度: 路径是由树中的两个结点之间的结点序列构成的. 而路径长度是路径上所经过的边的个数

而二叉搜索树的定义如下:
对一颗二叉树, 如果其所有结点node满足:

其左子树的所有结点, 其值均小于node.value
其左子树的所有结点, 其值均大于node.value

那么这棵树被称作二叉搜索树

下面是一个简易的BST模块:

private class BST<Key> {
    private Key key;
    private BST left;
    private BST right;

    public BST(Key key, BST left, BST Right) {
        this.key = key;
        this.left = left;
        this.right = right;
    }

    public BST(Key key) {
        this.key = key;
    }
}

BST的深度(Depth):

root的深度为0, 向下递增
BST的平均深度是所有结点的深度之平均值

BST的高度(Height): root到深度最大结点的距离, 也即树的最大深度.

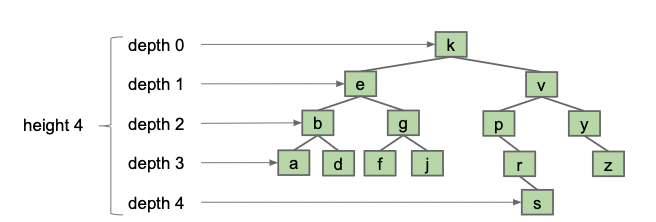
在BST的实际运行中, 其结点的深度决定了访问该结点所需的时间复杂度, 平均深度决定了BST的平均性能, 高度决定了BST的最坏运行时间. 在现实中, 我们可以证明:
对于一颗随机生成的BST, 记 \(N\) 为其结点数, \(h\), \(d\) 为表示其高度, 深度的随机变量, 我们有:

\[E[d]\approx 2\ln N\\ E[h]\approx 4.311\ln N \]

看似性能平均是对数级别的, 但在实际应用中, 我们无法做到真正意义上的“随机生成”(我们很多时候并不能一次性获得所有的数据, 而是不断的构建/优化BST), 所以, 采取必要的措施去保证BST的“bushiness“很重要.

1.2 BST的遍历方式

而对于一颗BST, 如果我们把“遍历根结点”“遍历左子树”“遍历右子树”分别称作“D”“L”“R”, 那么我们按照遍历的先后, 递归的分别有6种遍历方式: DLR, DRL, LDR, RDL, LRD, RLD.

而考虑到在L与R在树结构上的对称性, 先遍历L还是R塞算法设计上的差别不大, 我们只考虑三种遍历方式:

前序遍历(preorder traversal)-DLR
中序遍历(inorder traversal)-LDR
后序遍历(postorder traversal)-LRD

我们给出一个样例BST:

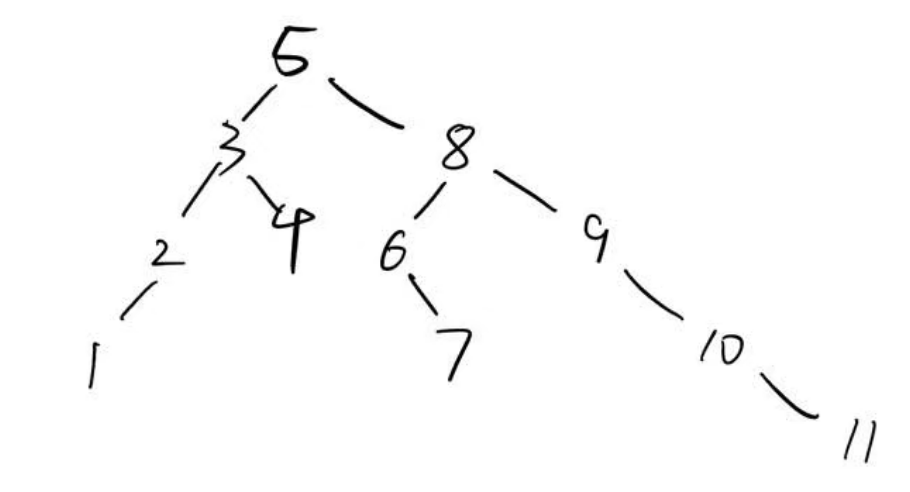
1.2.1 前序遍历

(我们仅解释一次, 后两种请自行类比)
对于每棵子树, 我们先遍历其根结点, 再依次遍历其左右子树.
对于样例BST, 我们的遍历顺序为:
5-3-2-1-4-8-6-7-9-10-11
example code:

def preorder_traversal(tree, oper):
   if tree == None: return
   oper(tree.node)
   preorderTraversal(tree.left, oper)
   preorderTraversal(tree.right, oper)

通常来说, 前序遍历因为其会先遍历到根结点, 所以常用于当子结点依赖于父结点的情况.

1.2.2 中序遍历

对于样例BST, 我们的遍历顺序为:
1-2-3-4-5-6-7-8-9-10-11
example code:

def inorder_traversal(tree, oper):
   if tree == None: return
   inorder_traversal(tree.left, oper)
   oper(tree.node)
   inorder_traversal(tree.right, oper)

采取LDR或者RDL, 可以实现对BST的有序遍历, 获得有序的结果.

1.2.3 后序遍历

对于样例BST, 我们的遍历顺序为:
1-2-4-3-7-6-11-10-9-8-5
example code

def postorder_traversal(tree, oper):
   if tree == None: return
   inorder_traversal(tree.left, oper)
   inorder_traversal(tree.right, oper)
   oper(tree.node)

2. B-Tree

我们考虑有一颗已经构建好的BST, 如图所示:

如果我们想向内插入新的元素8, 那么将会得到一颗高为4的新BST. 想象一个最糟糕的情况, 如果我们继续插入9,10,11..., 那么我们将会得到一个 \(h\approx N\) 的超高的BST, 此时它的性能将接近Linked List. 所以我们考虑一种“过度填充(Overstuffing)”的思路:
即将8与7放在同一个“格子”里(有点类似解决哈希碰撞的Chaining方法), 也就是得到如下右图的形式

但是面临上述情况时, 同样会遭遇退化成链表的问题, 为了解决这个问题, 我们考虑让格子中的元素“上浮”. 也即当叶子结点上元素过多时, 我们考虑向父结点上浮其中的元素.

另一个问题是, 当一个结点有多个元素时, 其BST的性质将会发生改变, 我们很麻烦才能判断围绕着个结点的大小关系. 故我们考虑采用这个策略:

对于每个有 \(n\) 个元素 \(\{a_1,a_2,...a_n\}\) 的父结点, 其应有 \(n+1\) 颗子B-Tree, 从左往右, 第 \(k\) 颗 \((0<k\le n)\) 子树中的任意元素 \(m\) 应满足 \(a_{k-1}(if\ exist)<m<a_k(if\ exist)\)
也即我们将该结点下所有元素划分成个区间, 以父结点所有元素作为这些区间的端点.
以下是严格定义

Definition:
m-n B-Tree是指每个节点至少有 \(m\) 个关键字, 最多有 \(n\) 个子结点(i.e. 最多 \(n-1\) 个关键字)的B-Tree

而B-Tree中有两个重要的不变量:

所有的叶子都离根的距离相同
具有 \(k\) 个项目的非叶子节点必须正好有 \(k+1\) 个子节点

我们接下来以依次插入1-9 9个元素为例, 分别演示2-4 B-Tree与3-6 B-Tree的构造过程:
(AI生成)
2-4 B-Tree:
✅ 插入 1

树为空，创建一个根节点，插入 1。

[1]

✅ 插入 2

根节点未满（最多 3 个键），插入 2。

[1, 2]

✅ 插入 3

根节点仍不满，插入 3。

[1, 2, 3]

❗插入 4

根节点已满（已有 3 个键），需要分裂（split）。
分裂规则：
将当前节点的中间键（即 2）上移。
左边键（1）作为一个新节点。
右边键（3, 4）作为另一个新节点。
新的根节点包含中间键 2。

     [2]
   /     \
[1]   [3, 4]

✅ 插入 5

找到应该插入的位置：右子节点 [3, 4]。
该节点未满，插入 5。

     [2]
   /     \
[1]   [3, 4, 5]

❗插入 6

插入到右子节点 [3, 4, 5]，该节点已满，需要分裂。
中间键是 4，上移到父节点。
左子节点：[3]
右子节点：[5, 6]
父节点 [2] 接收新键 4，变成 [2, 4]

       [2, 4]
     /   |   \
  [1]  [3]  [5, 6]

✅ 插入 7

找到应该插入的节点：最右边的叶子节点 [5, 6]。
该节点未满（最多 3 个键），插入 7。

       [2, 4]
     /   |   \
  [1]  [3]  [5, 6, 7]

❗ 插入 8

插入到 [5, 6, 7]，该节点已满（3 个键），需要分裂。
中间键：6，上移到父节点。
左子节点：[5]
右子节点：[7, 8]
父节点 [2, 4] 接收新键 6，变成 [2, 4, 6]

         [2, 4, 6]
       /   |   |   \
    [1]  [3] [5] [7, 8]

❗ 插入 9

插入到 [7, 8]，插入 9 后变成 [7, 8, 9]，未满 → 插入完成 ✅

         [2, 4, 6]
       /   |   |   \
    [1]  [3] [5] [7, 8, 9]

3-6 B-Tree
✅ 插入 1

树为空，创建根节点，插入 1。

[1]

✅ 插入 2

根节点未满（最多 5 个键），插入 2。

[1, 2]

✅ 插入 3

插入到根节点中。

[1, 2, 3]

✅ 插入 4

插入到根节点中。

[1, 2, 3, 4]

✅ 插入 5

插入后变成 [1, 2, 3, 4, 5]，未满。

[1, 2, 3, 4, 5]

❗ 插入 6

根节点已满（已有 5 个关键字），需要分裂（split）
找到中间键：3，作为新根
左子节点：[1, 2]
右子节点：[4, 5, 6]
新结构如下：

     [3]
   /     \
[1, 2]  [4, 5, 6]

✅ 插入 7

插入到右子节点 [4, 5, 6] 中 → 插入后变成 [4, 5, 6, 7]

     [3]
   /     \
[1, 2]  [4, 5, 6, 7]

✅ 插入 8

插入到右子节点中 → [4, 5, 6, 7, 8]

     [3]
   /     \
[1, 2]  [4, 5, 6, 7, 8]

❗ 插入 9

右子节点已满（5 个键），需要分裂
中间键：6
左子节点：[4, 5]
右子节点：[7, 8, 9]
父节点插入 6
父节点 [3] 接收新键，变为 [3, 6]


       [3, 6]
     /   |   \
[1,2] [4,5] [7,8,9]

最后, 我们简要的分析一下B-Tree的性能
对于一颗有 \(N\) 个元素 p-q B-tree,

高度
其高度应介于最好与最坏情况之间. 如果这颗B树是满的, 那么其高度应为 \(\log_q \frac{N}{q-1}\), 也即 \(\Omega(\log N)\) ; 对于其最坏情况, 即每个结点只有 \(p\) 个元素, 那么其高度应为 \(\log_{p+1}\frac{N}{p}=O(log N)\)
故B树的高度是 \(\Theta (\log N)\) 级别的
类似的分析, 其contain, add的的复杂度均为 \(O(\log N)\)

3. Red-Black Tree

PS. 本课(CS61B Lec18)中, 是基于对2-3 B-Tree的等价变形, 引出了LLRB(左倾红黑树), 并未介绍最原始的红黑树, 本笔记将基于本人对红黑树的学习, 将两种红黑树分别介绍

PS. 红黑树的发明晚于AVL, 其发明目的是基于简化AVL创建成本而诞生的, 但是由于其于B-Tree的等价关系, 故先收录红黑树.

本部分主要基于我对如下文章/网页/工具的学习:
【数据结构】史上最好理解的红黑树讲解，让你彻底搞懂红黑树 - 小七mod

红黑树, 是一种自平衡的二叉查找树, 是一种高效的查找树. 由Rudolf Bayer于1972年发明的, 当时被称作“平衡二叉 B 树(symmetric binary B-trees)“, 后来在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树.

我们前面已经说明了(并未证明), 如果一颗BST是随机生成的, 那么其高度在 \(O(\log n)\) 范围内, 但在实际应用中, 数据的输入是不断进行的, 且通常是部分有序的(这也是python采用Tim排序的原因), 最极端情况下, 如果数据的输入是完全有序的, 那么BST将退化成一个链表, 达到 \(O(n)\) 性能, 失去了其性能的优势 (我们也可以说BST的实际性能在 \(O(\log n)\) 与 \(O(n)\) 之间).

为了避免这一情况, 我们考虑通过特殊的约定(红黑节点)+旋转操作, 达成在构建时高效的保持搜索树平衡.

我们约定:

3.1 红黑树的约束:

每个节点不仅保存值, 还保存其颜色(Red or Black)
叶子结点 (这里指null节点) 与 root 是黑色的
红色节点的 父结点 与 子结点 都是黑色的
1. 也即不存在相连的的红色节点
从任一节点到所有(能到达)叶子结点的简单路径(也即只能向下)上都有相同数目的黑色节点.
1. 我们将黑色节点的数目称为 “黑高(Black-Height)“bh(x)

而结合这几条约定, 我们能得出关于红黑树的许多有益性质:

3.2 红黑树的性质

(1) 任何一条从根到叶结点的简单路径上, 最长路径不大于最短路径的2倍

proof:
考虑约定4, 每条如上所示的路径上均有相同数目的黑色节点
考虑约定3, 无相邻的红色节点
故我们考虑最极端情况, 两条黑色节点数目相同的路径, 一条无红色节点, 一条塞满红色节点, 则后者是前者的二倍, 因为只能做到红黑相间.

(2) 红黑树的高度满足: \(n\le 2^{\frac{H}{2}}+ \frac{H}{2} -1\)

我们考虑最坏情况, 也即这颗红黑树只有一条路径是红黑相间的, 剩下的路径均为全黑, 也即有:

\[n=(2^{\frac{H}{2}}-1)(前\frac{H}{2}层)+\frac{H}{2}(最长路径中比\frac{H}{2}更深的部分)\\ =2^{\frac{H}{2}}+ \frac{H}{2} -1 \]

考虑最好情况, 这棵树的所有由跟到叶子结点的路径均相同

\[n = 2^{\frac{H}{2}}-1 \]

故, 对于所有的红黑树, 我们有:

\[2^{\frac{H}{2}}-1 \le n \le 2^{\frac{H}{2}}+ \frac{H}{2} -1 \]

化简有:

\[H \le 2\log_2 (n+1)\Leftrightarrow H=O(\log(n+1)) \]

而在 \(H\) 充分大时, 与 \(2^{\frac{H}{2}}\) 相比, \(\frac{H}{2}\) 可以近似忽略, 我们就可以得出:

\[H=\Theta(\log(n+1)) \]

从理论上分析, 每个结点的黑高均相等, 每个结点都有0-4个子树, 这都完美符合的2-4B树的定义.
换句话说, 红黑树和2-4 B树是存在一一对应关系的, 其中对应的每个B树, 其节点都是黑色结点在中间, 红色结点在左右的结构.

3.3 等价变换

虽然B树和红黑树的基于不同的目的分别独立的发明出来的

红黑树为简化AVL的维护
B树为优化硬盘储存空间检索

但是我们发现红黑树和B树是存在某种等价关系的. 对于一颗红黑树, 当我们将其所有的红色节点移动至其父结点“Overstuffing”时, 我们发现事实上我们新得到的结构就是一颗 2-4 B树, 如下图所示

3.4 构建/维护红黑树

我们先详细讲解释一下几个基本操作:

3.4.1 旋转操作

我们的旋转是针对某个结点进行的, 对每个节点, 只要其左子树非空即可左旋(也即以其右子结点代替其本身位置), 右旋同理.
而旋转 不应破坏BST本身的性质 , 故我们在更换结点后,还有移植子树的操作.

picture

具体的过程是:

picture

! 这里的旋转操作不止局限于红黑树, 后面讲到的AVL同样基于旋转操作来维护BST的性质

3.4.2 查找操作

同普通BST的查找, 因为红黑树与AVL本身就是 有更多优化约束的BST

3.4.3 插入操作(重点)

我们知道红黑树与2-4B树是具有一一对应的关系的. 如果我们以2-4B树的视角来看, 我们会很轻易的通过我们对B树的了解, 先转换成B树, 再进行插入删除操作, 最后再转回红黑树, 但这本身就与我们 简化AVL插入删除繁琐过程 的初衷相悖. 所以我们仅以红黑树本身变形的视角进行解释, 中间以2-4B树的视角进行等价的辅助说明.

step1. 我们规定, 每个新插入的结点都是红色结点

这一条看起来似乎与红黑树的几条性质相左, 我们在后续的步骤中, 会涉及染色操作, 从而保持红黑树的性质不变

step2. 将新插入的结点放置在相应的叶子结点位置上

step3. 调整直至新BST满足红黑树性质

我们先统一一下BST的辈份www

(左右顺序可换, 但称谓不分左右, 看以哪个子结点为主视角)

此后, 我们会遇到很多种情况需要分别讨论.

插入结点时为root, 则变为黑色, 结束.
1. 2-4B树视角: 根结点一定是结点中最中间的结点
若父结点是黑色, 则不违背红黑树性质, 结束.
1. 2-4B树视角: 也即此叶子结点只有一个值, 我们只需overstuff插入进该结点即可
若叔叔节点(父结点的同父兄弟结点)为黑色:
1. LL类型, 即新结点为父结点的左子结点, 父结点为祖父结点的左子结点(之后将不再解释)
  1. 首先对祖父进行右旋
  2. 原来的父, 爷结点变色
  3. 得到红黑树
  1. 2-4B树视角:
2. LR类型
  1. 先对父结点进行左旋
  2. 然后得到同3.1的LL类型, 相似处理方式
1. RR类型
  1. 首先对祖父进行左旋
  2. 原来的父, 爷结点变色
  3. 得到红黑树
1. RL类型
  1. 先对父结点进行右旋
  2. 然后得到同3.3的RR类型, 相似处理方式
若叔叔节点为红色
这种情况只需要变色即可
1. 将父结点, 叔叔节点, 租父结点变色
2. 若租父结点为root, 则染上黑色.
  下图例为假设租父结点不是root的情况

3.4.4 删除操作

红黑树的删除情况较为复杂, 不过类似插入, 我们先类似BST的删除找到结点, 然后删除结点, 并通过染色+旋转操作从而恢复红黑树的性质
参考链接:

彻底理解红黑树（三）之删除

以及附上一张, 大部分情况(对于实现完BST的插入/删除后不符合红黑树约定的情况), 变形直至恢复红黑树性质的图片

3.5 红黑树效率

每次旋转只需要常数时间 \(O(1)\)
每次查找需要 \(O(\log n)\)时间
由性质3.2.(2)可知, 树的高度是 \(\Theta(\log(n+1))\), 由此可知, 查找的最坏情况也是 \(\Theta(\log(n+1))\) 级别的时间.
每次插入/删除最多耗费 \(O(\log n)+O(1)=O(\log n)\) 时间.
因为只需要查找到相应叶子位置+常数级别的旋转/染色时间(因为没有循环, 递归之类的操作)

3.6 左倾红黑树 LLRB Tree (Left Leaning Red-Black tree)

PS. 这也是CS61B主讲的红黑树, 本人猜测是因为其原理与标准红黑树类似, 但是实现更简单, 更具有教学意义而非工程实践意义.

左倾红黑树与 2-3 B树 有一一对应的关系, 每个多元素结点(最多两个元素), 左元素被划分为红结点连至左子树, 右元素被划分为黑结点保留. 从而得到了相应的BST.

与传统“standard RBTree”相比, LLRB Tree实现起来更加的简便(重点在插入/删除上), 它简化了一部分的约束

“它满足了许多原始设计目标，并且导致插入/删除的代码简单的多，仅需要常用实现代码的四分之一“
具体来说，在由一个N个键构成的左倾红黑2-3树种，一个搜索操作需要检查lgN - 0.5个节点，树的平均高度约为 \(2\ln n\)
在LLRB中由许多吸引人的特性：
1：实验研究未能将这些算法与最优算法区分开
2：它可以通过向标准BST算法添加几行代码来实现。
3：与哈希表不同，他们支持有序操作，如：SELECT，RANK，RANGE搜索
因此LLRB树对于各种符号表应用程序都很有用，并且是未来软件库中作为符号表基础的主要候选对象
--(LLRB 发明者 Robert Sedgwick)

左倾红黑树有如下几条简化的不变量约束:

root与叶子结点(Null)是黑色的
不存在两个相邻的红色结点
每条路径上的黑色结点的数量是相同的

其操作的思想也与标准红黑树类似, 我们这里就不再展开赘述了.

4. AVL

AVL是 平衡二叉树 全称叫做 平衡二叉搜索(排序)树, 简称 AVL树(Balanced Binary Tree)
AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写, 他们提出的平衡二叉树的概念, 为了纪念他们, 将平衡二叉树称为 AVL树

4.1 definition

我们定义:
一个结点的 “倾斜(skew)” , 为其左子树的高度减其右子树的高度.
我们继续定义:
我们称一个结点是 高度平衡的(height-balanced) , 当且仅当其 \(skew \in \{-1, 0, 1\}\)

一颗AVL树, 其左右子树都是AVL树

4.2 AVL的性质

基于先前所述的性质, 我们可以推出一个重要的结论: AVL树是平衡的.
i.e. AVL树的平均高度为 \(O(\log n)\) 级别
proof:
该树的高度 \(h=O(\log n)\)等价于对于结点数 \(n\) 有 \(n=2^{\Omega(h)}\);
我们假设 \(F(h)\) 表示, 一颗高度为 \(h\) 的AVL的最少结点数字.
那么有:

\[\begin{aligned} &F(0) &&=0\\ &F(1) &&=1\\ &F(h) &&=1+F(h-1)+F(h-2)(由于AVL的性质)\\ &\ &&\ge 2F(h-2) \end{aligned} \]

故我们有:

\[\begin{aligned} F(h)\ge2^(\frac{h}{2})\\ 也即: F(h)=2^{\Omega(h)} \end{aligned} \]

这样我们证明了, 这个重要性质. 而我们接下来关注, 如何构建一颗AVL树, 以及如何在insert/delete中保持其性质

4.3 维护AVL

在每次的插入过程中, 其只有可能影响其直系长辈结点的height-balance. 所以我们只需要关注其长辈结点.
并且, 对于一颗skew为 \(\pm2\) 的不平衡AVL, 当我们通过旋转的方式消除不“高度平衡”性时, 其本身的高度也就减少了1(if L=D+2, then L'->L-1 = D+1; D'->D+1=L', height:D+2->D+1).所以我们只需找到这个叶子结点最近的不平衡祖先结点, 通过旋转将其平衡, 则不会对其祖先的祖先的平衡性造成影响.

确定了这一点, 我们发现, 只要能找到该祖先结点, 就能以 \(O(1)\) 的时间成本解决, 也即插入时的时间成本主要花费在寻找该祖先结点上.

更具体的, 不妨设找到高度为 \(h\) 的结点的skew成本为 \(T(h)\), 那么我们有:

\[time = O(\sum^h_{i=0}T(i)+1)=O(\sum^h_{i=0}T(i)) \]

我们找到每个结点左右子树的时间复杂度是 \(\Omega(\log n)\).
example code:

def height(tree):
   if tree == None: return 0
   return height(tree.left) + height(tree.right) + 1

则有:

\[time = O(\log n!)\approx O(n\log n) \]

花销很大, 那么我们考虑令每个结点都储存自身的高度, 达到需要时 \(O(1)\) 的访问, 并在插入/删除是自动维护数值, 从而减小开销

以下是具体的实现(provide by mit6.006)

Binary Node Implementation with AVL Balancing

def height(A):
    if A:
        return A.height
    else:
        return -1


class Binary_Node:
    def __init__(A, x):  # O(1)
        A.item = x
        A.left = None
        A.right = None
        A.parent = None
        A.subtree_update()

    def subtree_update(A):  # O(1)
        A.height = 1 + max(height(A.left), height(A.right))

    def skew(A):  # O(1)
        return height(A.right) - height(A.left)

    def subtree_iter(A):  # O(n)
        if A.left:
            yield from A.left.subtree_iter()
        yield A
        if A.right:
            yield from A.right.subtree_iter()

    def subtree_first(A):  # O(log n)
        if A.left:
            return A.left.subtree_first()
        else:
            return A

    def subtree_last(A):  # O(log n)
        if A.right:
            return A.right.subtree_last()
        else:
            return A

    def successor(A):  # O(log n)
        if A.right:
            return A.right.subtree_first()
        while A.parent and (A is A.parent.right):
            A = A.parent
        return A.parent

    def predecessor(A):  # O(log n)
        if A.left:
            return A.left.subtree_last()
        while A.parent and (A is A.parent.left):
            A = A.parent
        return A.parent

    def subtree_insert_before(A, B):  # O(log n)
        if A.left:
            A = A.left.subtree_last()
            A.right, B.parent = B, A
        else:
            A.left, B.parent = B, A
        A.maintain()

    def subtree_insert_after(A, B):  # O(log n)
        if A.right:
            A = A.right.subtree_first()
            A.left, B.parent = B, A
        else:
            A.right, B.parent = B, A
        A.maintain()

    def subtree_delete(A):  # O(log n)
        if A.left or A.right:
            if A.left:
                B = A.predecessor()
            else:
                B = A.successor()
            A.item, B.item = B.item, A.item
            return B.subtree_delete()
        if A.parent:
            if A.parent.left is A:
                A.parent.left = None
            else:
                A.parent.right = None
            A.parent.maintain()
        return A

    def subtree_rotate_right(D):  # O(1)
        assert D.left
        B, E = D.left, D.right
        A, C = B.left, B.right
        D, B = B, D
        D.item, B.item = B.item, D.item
        B.left, B.right = A, D
        D.left, D.right = C, E
        if A:
            A.parent = B
        if E:
            E.parent = D
        B.subtree_update()
        D.subtree_update()

    def subtree_rotate_left(B):  # O(1)
        assert B.right
        A, D = B.left, B.right
        C, E = D.left, D.right
        B, D = D, B
        B.item, D.item = D.item, B.item
        D.left, D.right = B, E
        B.left, B.right = A, C
        if A:
            A.parent = B
        if E:
            E.parent = D
        B.subtree_update()
        D.subtree_update()

    def rebalance(A):  # O(1)
        if A.skew() == 2:
            if A.right.skew() < 0:
                A.right.subtree_rotate_right()
            A.subtree_rotate_left()
        elif A.skew() == -2:
            if A.left.skew() > 0:
                A.left.subtree_rotate_left()
            A.subtree_rotate_right()

    def maintain(A):  # O(log n)
        A.rebalance()
        A.subtree_update()
        if A.parent:
            A.parent.maintain()

posted on 2025-08-05 18:45 dddsx259 阅读(18) 评论(0) 收藏举报

刷新页面返回顶部

dddsx259

导航

公告

Search Tree

Search Tree

1. 二叉搜索树 BST(Binary Search Tree)

1.1 BST的相关定义

1.2 BST的遍历方式

1.2.1 前序遍历

1.2.2 中序遍历

1.2.3 后序遍历

2. B-Tree

3. Red-Black Tree

3.1 红黑树的约束:

3.2 红黑树的性质

(1) 任何一条从根到叶结点的简单路径上, 最长路径不大于最短路径的2倍

(2) 红黑树的高度满足: \(n\le 2^{\frac{H}{2}}+ \frac{H}{2} -1\)

3.3 等价变换

3.4 构建/维护红黑树

3.4.1 旋转操作

picture

picture

! 这里的旋转操作不止局限于红黑树, 后面讲到的AVL同样基于旋转操作来维护BST的性质

3.4.2 查找操作

3.4.3 插入操作(重点)

step1. 我们规定, 每个新插入的结点都是红色结点

step2. 将新插入的结点放置在相应的叶子结点位置上

step3. 调整直至新BST满足红黑树性质

3.4.4 删除操作

3.5 红黑树效率

3.6 左倾红黑树 LLRB Tree (Left Leaning Red-Black tree)

4. AVL

4.1 definition

一颗AVL树, 其左右子树都是AVL树

4.2 AVL的性质

4.3 维护AVL

Binary Node Implementation with AVL Balancing