动态规划
线性DP
线性模型

例题:
poj3486 Computers
你要保证 n 年中你都有一台电脑,一开始你有一台。 如果在第 y (1 <=y<=n) 年购买了一台,则需要花费 c 的代价。 如果这台电脑用到了第 z 年,在第 z 年又买了一台,你需要支付 m(y,z) 的维 修费用。 给定 n, c, 数组 m。求最小花费。
in: 3 3 5 7 50 6 8 1 0 out: 1 9
hint:第一年买一台:花费3
之前维修费用 m(1 ,1 )=5
第三年买一台,花费3
之前维修费用 m(2,3)=8
总费用: 3+5+3+8=1 9
解题思路:
每一年相当于一个阶段。 设 f[i] 表示到第 i 年累计的最小花费。 考虑 f[i] 是怎么转移过来的。 只需要枚举上一次买电脑是第几年即可。 假设上一次是第 j 年,那到第 i 年维修费用是 m(j, i), 花费为 c。 因此可以用 f[j-1 ]+m(j,i)+c 更新 f[i]。 转移方程: f[i] = min{ f[j-1 ]+m(j,i)+c | 1 <=j<=i }
时间复杂度 O(n^2).
代码:
#include <cstdio> #include <algorithm> #include <cstring> using namespace std; const int maxn = 1005; int c, y; int m[maxn][maxn]; int dp[maxn]; int main(void) { while(~scanf("%d", &c)) { scanf("%d", &y); for(int i = 1; i <= y; ++i) { for(int j = i; j <= y; ++j) { scanf("%d", &m[i][j]); } } memset(dp, 0x3f, sizeof(dp)); dp[0] = 0; for(int i = 1; i <= y; ++i) { for(int j = 1; j <= i; ++j) { dp[i] = min(dp[i], dp[j-1]+c+m[j][i]); } } printf("%d\n", dp[y]); } return 0; }
区间DP区间模型

例题:
bzoj1 786 配对
有一个长度为 n 的序列,每个数都是 1 ~K 中的整数。 现在有一些位置的数被遮住了,用 -1 表示。 你可以往这些位置填 1 ~K 中的数,使得整个序列的逆序对数最小,求最小的 逆序对数。
N<=1 0000, K<=1 00
解题思路:
考虑会形成逆序对的情况:
1、原有数形成逆序对。
2、填进去的数与原有数形成逆序对。
3、填进去的数之间形成逆序对。 很显然,为使逆序对数量尽可能少,填进去的数一定是单调不降的。 设 f[i][j] 表示填到第 i 个数且这位填数字 j 产生的逆序对数。 要计算 f[i][j], 只需考虑对原序列产生的贡献,
即 [1 ,i-1 ] 大于 j 的个数和 [i+1 ,n] 中小于 j 的个数。
设 g[i][j] 表示前者, l[i][j] 表示后者。 因此转移方程 f[i][j] = min{ f[i-1 ][k]+g[i][j]+l[i][j] }.
最后再加上数列本身的逆序对数就行。
核心代码:

背包DP
完全背包 例:
【题目描述】
n个重量和价值分别为Wi,Vi的物品,现从这些物品中挑选出总量刚好为 W 的 物品,求所有方案中价值总和的最大值。
【输入格式】 包含多组测试用例,每一例的开头为两位整数 n、 W. 接下来有 n 行,每一行有两位整数 Wi、 Vi。
【输出格式】 对每组数据,输出一行,即所有方案中价值总和的最大值。若不存在刚好填 满的情况,输出“-1”。
【数据范围】 1 < = n < = 1 0000,1 < =W< = 1 000,1 < =Wi < = 1 0000,1 < =Vi < = 1 00
【输入样例】
3 4 1 2 2 5 2 1 3 4 1 2 2 5 5 1
【输出样例】
6-1
解题思路:
这类问题在于dp数组的初始化。
恰好装满背包:则初始化时, DP[0]=0, 其他的DP[1… ..V]均设为负无穷大。
无须恰好装满背包:则初始化时, DP[1… ..V]全部设为0;
然后照常跑背包即可。
多重背包问题的单调队列优化
考虑 f[i][j], 令 b[i] = min(a[i], j/c[i]) f[i][j] = max(f[i-1 ][j-k*c[i]]+k*w[i]) (0<=k<=b[i])
发现对于 j-k*c[i] (0<=k<=b[i]) ,这些数 mod c[i] 都是同余的。 于是令 mod = j%c[i], div= j/c[i], 则 j = div*c[i] + mod
则
f[i][j] = max(f[i-1 ][mod+(div-k)*c[i]] + k*w[i]) (0<=k<=b[i])
令 t = div-k
则
f[i][j] = max(f[i-1 ][mod+t*c[i]] + (div-t)*w[i]) (div-b[i]<=t<=div)
对于第 i 个物品, div的值固定,跟选择 k 个的策略无关。 故最终有:
f[i][j] = max(f[i-1 ][mod+t*c[i]]-t*w[i]) + div*w[i] (div-b[i]<=t<=div)
考虑mod+t*c[i] 取值 (div-b[i] <= t <= b[i]) {mod, mod+c[i], mod+2c[i], mod+3c[i], ... j}
则 f[i][j] 就是求 j 前面共 b[i]+1 个数对应的 f[i-1 ][mod+t*c[i]]-t*w[i] 的最大值。
因为 b[i] = min(a[i], j/c[i]),则对于固定的 i , b[i]+1 是固定的。 因此,问题转化为求一个固定长度的滑动窗口的最大值问题。 维护一个单调下降的队列,枚举 mod, 再枚举 div, 则求 f[i][j] 是用单调队列, 复杂度O(m), 不同mod 和 div 对应一个 j, 总复杂度即是O(nm).
分组背包
• 分组背包,就是将物品分组,每组的物品相互冲突,最多只能选一个物品放 进去。
• 这类题就是从「在所有物品中选择一件」变成了「从当前组中选择一件」, 于是就对每一组进行一次 0-1 背包就可以了。
• 核心代码:
• for (int k = 1 ; k <= ts; k++) // 循环每一组
• for (int i = m; i >= 0; i--) // 循环背包容量
• for (int j = 1 ; j <= cnt[k]; j++) // 循环该组的每一个物品, t[k][j]表示第k组 第j号物品
• if (i >= w[t[k][j]]) • dp[i] = max(dp[i], dp[i - w[t[k][j]]] + c[t[k][j]]); // 像0-1背包一样状态转移
有依赖的背包
• 这种背包问题其实就是如果选第 i件物品,就必须选第 j件物品,保证不会循 环引用,一部分题目甚至会出现多叉树的引用形式。为了方便,就称不依赖 于别的物品的物品称为「主件」,依赖于某主件的物品称为「附件」。
• 对于包含一个主件和若干个附件的集合有以下可能性:仅选择主件,选择主 件后再选择一个附件,选择主件后再选择两个附件……需要将以上可能性的 容量和价值转换成一件件物品。因为这几种可能性只能选一种,所以可以将 这看成分组背包。
• 如果是多叉树的集合,则要先算子节点的集合,最后算父节点的集合。
树形dp
• 树形dp指状态图是一棵树,状态转移也发生在树上。
• 父节点的值通过所有子节点得到,一般在dfs的过程中完成dp。
void dfs(u){
for v in u.child: dfs(v) use dp[v] to update dp[u]
}
树上最长链
给定一棵树,每条边有边权,计算一条最长链。 要求时间复杂度为O(n)。
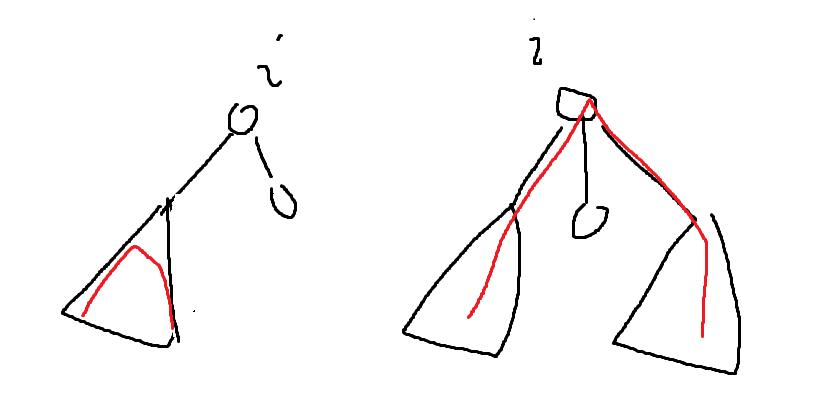
定义 f[i] 是以 i 为根的子树中的最长链。 显然 f[i] = max(f[i], f[j]) (j 是 i 的子节点) 但这样只考虑了不经过 i 的路径,如右图。 如果要考虑经过 i 的路径,就需要选择两个子节点。 把两个子节点往下走的最长路相加,再加上它们到 i 的路径和,去更新 f[i]。 定义 g[i] 表示从 i 往下走最远能走多少。
g[i] = max(g[i], g[j] + w(i, j)) (j 是 i 的子节点) 对于叶节点 f = g = 0

数位dp
• 问题的形式一般是:
• 定义一个条件 A,比如:被 7 整除,数位中含有 3 等等。
• 然后询问区间 [L, R] 中有几个数满足 A。
• L 和 R 的范围一般非常大,比如1 0^1 8。
• 数位 dp 就是考虑数字的每一位,问题规模变为 lgn. • 每一位作为不同的阶段,设计状态。
• 我们从高位往低位依次枚举。 (为什么不选择从低位到高位枚举?)
• 比如 N = 1 230. • 假设前两位枚举的是 1 和 2,也就是计算了1 2开头的贡献。
• 此时枚举第三位,可选范围只要 0 ~ 3。
• 如果前两位枚举的是 1 和 0 ,则第三位范围为 0 ~ 9. • 因此我们用一个变量 eq 或 less表示在枚举当前位之前每一位是不是都和N
选的一样。
• 当前设为第 dep 位, N 的第dep位为 A[dep], 假设填上 k,
• 如果采用 eq 变量:
eq = (eq && A[dep]==k)
可选最大值是 eq ? A[dep] : 9
如果采用 less 变量:
less = (less || k < A[dep])
可选最大值是 less ? 9 : A[dep]
• 为了直观理解数位dp,我们采用记忆化搜索形式,高位答案由低位答案转移 而来。
状压dp
• 顾名思义,就是把状态压缩起来。
• 比如对于 8*8 的棋盘,每个位置可以放一个棋子,对于在第 i 行第 2 个位置 和第 6 个位置放了棋子,我们可能需要8维或9维的数组去表示。
• 因此我们就有了把一行状态压缩成一个数字的做法。
• 一般我们会转化为二进制,如果每个位置可以有 3 种状态,那我们可以采用 三进制。
• 这样只需要一个大小为2^8的一维数组我们就可以存下所有状态。
• 这就是状态压缩。
DP基础优化
LIS的O(nlgn)算法
• 设 d[i] 为以i结尾最长上升子序列长度。
• 注意到如果 a[i] < a[j] 且 d[i] = d[j],那么对于后续的状态 k(k > i && k > j)来说 , i 不会比 j 差(即如果j满足 a[j] < a[k],那i一定满足,反之却不一定),因 此,我们只需保留 i 这个状态,一定不会损失最优解。
• 因此对于相同的 d 值,只需保留最小的 a[i] 即可。
• 设 g[i] 为长度为 i 的子序列末尾的最小值,显然 g 是单调的,
g[1 ]<=g[2]<=g[3]… • 随着 i 值增大, g 也会动态改变。
• 给定状态 i,我们可以二分查找 g 中第一个大于等于 a[i] 的下标k,则有:
• d[i] = k,此时需要更新 g[k] = a[i].
核心代码如下:

• 如果求不下降子序列呢?
• 将lower_bound换成upper_bound即可。
• 缺点:
• 只能求结果长度,很难去输出该序列。
dp的滚动数组优化
比如有一个二维的 dp 数组 f[i][j].
在转移过程中发现 f[i][j] 都是从 f[i-1 ][j] 转移过来的,并且在算 f[i][*] 时之前的 所有的 f[i-1 ][*] 已经全部算好。 那么这个时候就可以把第一维的空间”滚动“掉。 因为 f[i-1 ][*] 更新完 f[i][*] 后就没有用了。 具体实现可以用两个数组 f 和 g 轮换着更新:


dp的矩阵乘法优化
首先先要会矩阵乘法和矩阵快速幂和构造转移矩阵。 对于二维以上的 dp,如 f[i][j][k], 如果它全部由 f[i-1 ] 转移过来,则我们可以构 造转移矩阵来加速。 即把 f[i] 压缩成一维数组, f[i-1 ] 也压缩成一维数组。 转移方程就相当于 f[i] = f[i-1 ]*转移矩阵。 比如 f[i][t] += f[i-1 ][s], 那么转移矩阵第 s 行第 t 列元素就要加1 .
这样对于转移 n 次的 dp, 我们只需要计算转移矩阵的 n 次幂即可。 时间复杂度可以从 O(n) 优化为 O(logn)。
dp单调性优化
斜率优化dp
首先决策是单调的,然后可以用单调性来快速跳过冗余的决策。
dp的单调队列优化
所谓的单调队列优化dp等也不过是列完转移方程后然后可以转化为一个左右 端点递增的区间询问最值的问题罢了。
区间dp的O(n^2)算法(四边形不等式优化)
考虑区间 dp 方程
f[i][j] = min(f[i][k] + f[k+1 ][j] + w[i][j))
对于每个区间都要枚举 k,因此时间复杂度O(n^3)。 我们发现状态数已经定好了是O(n^2),所以只能从枚举的 k 次数入手,将其优 化到O(1 )。 这里就要用到四边形不等式优化。
首先四边形不等式的式子: 对于任意的 a < b < c < d, 如果有 f(a, c) + f(b, d) <= f(b, c) + f(a, d), 那么我们即称 f 满足四边形不等式。 简易记忆即交叉之和小于包含之和。
如果代价函数 w(i, j) 满足单调性和四边形不等式,则 dp 函数 f(i, j)也满足四 边形不等式。 定义 s(i, j) 为 f(i, j) 取得最优值对应的转移(即最优的 k) 如果 f(i, j) 满足四边形不等式,那么 s(i, j) 单调,即
s(i, j) <= s(i, j+1 ) <= s(i+1 , j+1 ).





 浙公网安备 33010602011771号
浙公网安备 33010602011771号