树形结构2

可持久化线段树

概念：可持久化线段树又被称为主席树。可持久化是指更新的同时保留了历史版本，可以获得所有的历史版本。本质上是多棵线段树，不过这些线段树共同使用了一部分枝干。

实现：可持久化线段树和线段树的实现有很大差别。线段树的

left和right表示区间的左右边界，而可持久化线段树的left和right

表示该节点的左右儿子。每更新一次，新建log(n)条边。

 

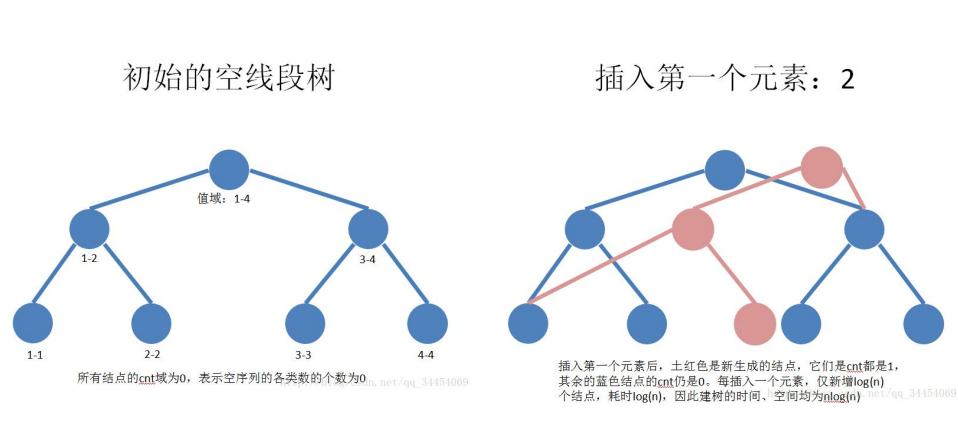
 模板题：P3919 可持久化线段树 1

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;

const int N=1e6+1;
#define L t[i].l
#define R t[i].r

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
    int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

struct tree {
    int l,r,num;
};
tree t[N<<4]; int a[N];
int n,m,root[N<<4],f=0;

inline int ins(int i) {
    t[++f]=t[i]; return f;
}

inline int build_tree(int i,int l,int r) {
//    printf("%d %d %d\n",i,l,r);
    i=++f; if(l==r) {
        t[i].num=a[l]; return f;
    } int mid=(l+r)>>1;
    L=build_tree(L,l,mid);
    R=build_tree(R,mid+1,r);
    return i;
} //建树

inline int update(int i,int l,int r,int x,int y) {
//    printf("%d %d %d\n",i,x,y);
    i=ins(i); if(l==r) {t[i].num=y; return i;}
    int mid=(l+r)>>1;
    if(x<=mid) L=update(L,l,mid,x,y);
    else R=update(R,mid+1,r,x,y);
    return i;
} //修改

inline int query(int i,int l,int r,int x) {
//    printf("%d %d\n",i,x);
    if(l==r) return t[i].num;
    int mid=(l+r)>>1;
    if(x<=mid) return query(L,l,mid,x);
    else return query(R,mid+1,r,x);
} //查询

int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    root[0]=build_tree(0,1,n); //先建一棵树
    for(int i=1;i<=m;i++) {
        int op=read(),x=read(),y=read(),k;
        if(x==1) {
            k=read();
            root[i]=update(root[op],1,n,y,k); //每次多建一棵
        } else {
            printf("%d\n",query(root[op],1,n,y));
            root[i]=root[op]; //多建一棵
        }
    }
    return 0;
}

 

树状数组

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

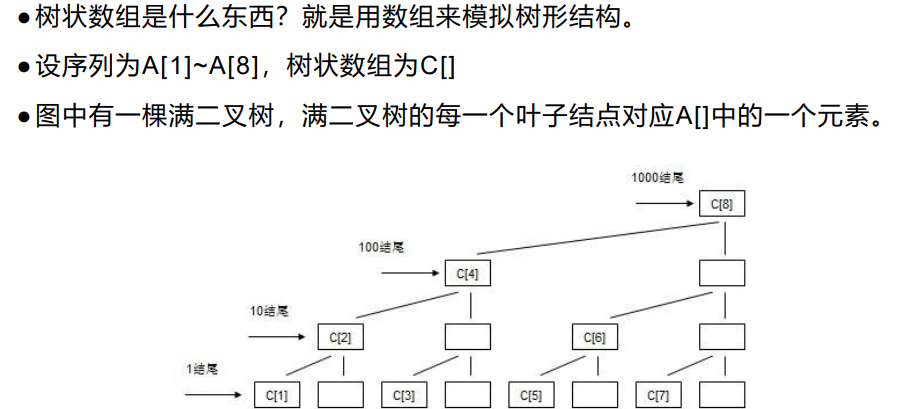
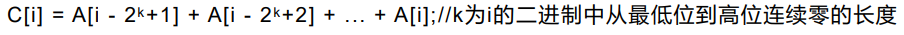
二.

 

 

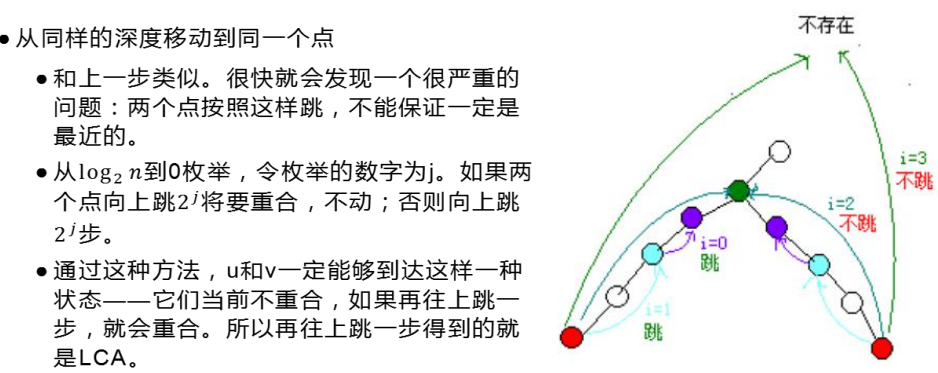
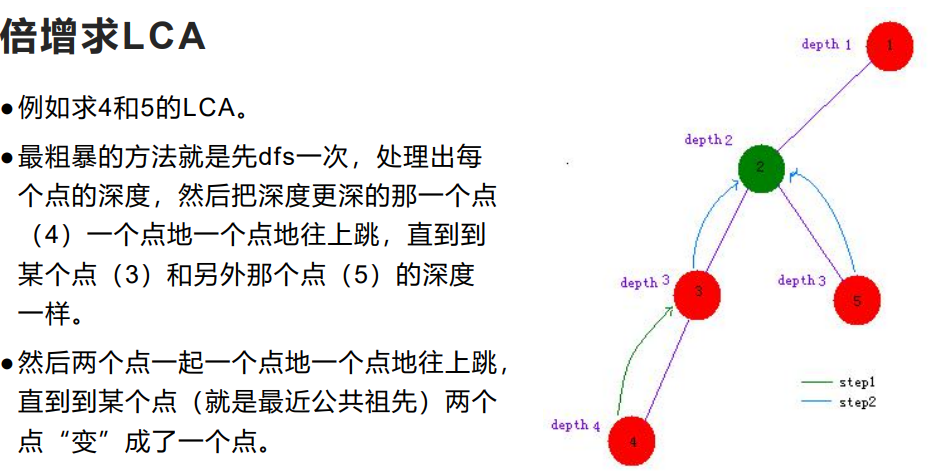
 LCA模板题：洛谷P3379

#include <iostream>
#include <cstdio>
#include <cstring>
 
using namespace std;
const int maxN = 500005;
 
inline int read()
{
    int x = 0, f = 1; char c = getchar();
    while(c < '0' || c > '9') { if(c == '-') f = -f; c = getchar(); }
    while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}
 
struct EDGE{
    int adj, to;
    EDGE(int a = -1, int b = 0): adj(a), to(b) {}
}edge[maxN << 1];
int head[maxN], cnt;
 
void init()
{
    memset(head, -1, sizeof(head));
    cnt = 0;
}
 
void add_edge(int u, int v)
{
    edge[cnt] = EDGE(head[u], v);
    head[u] = cnt ++ ;
}
 
int deep[maxN], f[maxN][21], n, m, root;
 
void dfs(int u, int fa)
{
    deep[u] = deep[fa] + 1;
    f[u][0] = fa;
    for(int i = head[u]; ~i; i = edge[i].adj)
    {
        if(edge[i].to == fa)
            continue;
        dfs(edge[i].to, u);
    }
}
 
void LCA_pre()
{
    deep[0] = 0;
    dfs(root, 0);
    for(int i = 1; i <= 20; ++ i )
        for(int u = 1; u <= n; ++ u ) //放在内层循环，保证每一层的结点都更新完才更新下一层
            f[u][i] = f[f[u][i - 1]][i - 1];
}
 
int LCA(int u, int v)
{
    if(deep[u] < deep[v]) swap(u, v); //保证deep[u] > deep[v]
    for(int i = 20; i >= 0; -- i )
    {
        if(deep[f[u][i]] >= deep[v])
            u = f[u][i];
    }
    if(u == v) return u;
    for(int i = 20; i >= 0; -- i )
    {
        if(f[u][i] != f[v][i])
        {
            u = f[u][i];
            v = f[v][i];
        }
    }
    return f[u][0];
}
 
int main()
{
    init();
    n = read(); m = read(); root = read();
    for(int i = 0; i < n - 1; ++ i )
    {
        int u, v; u = read(); v = read();
        add_edge(u, v);
        add_edge(v, u);
    }
    LCA_pre();
    for(int i = 0; i < m; ++ i )
    {
        int u, v; u = read(); v = read();
        printf("%d\n", LCA(u, v));
    }
    return 0;
}

 

 

 

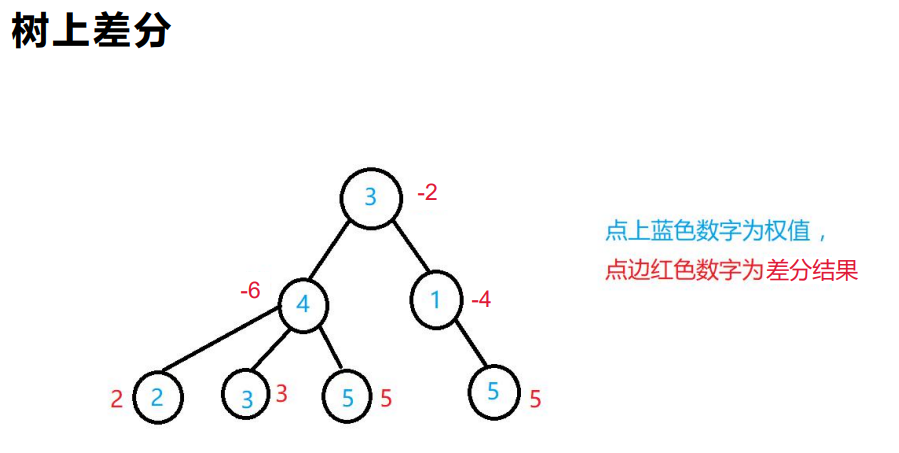
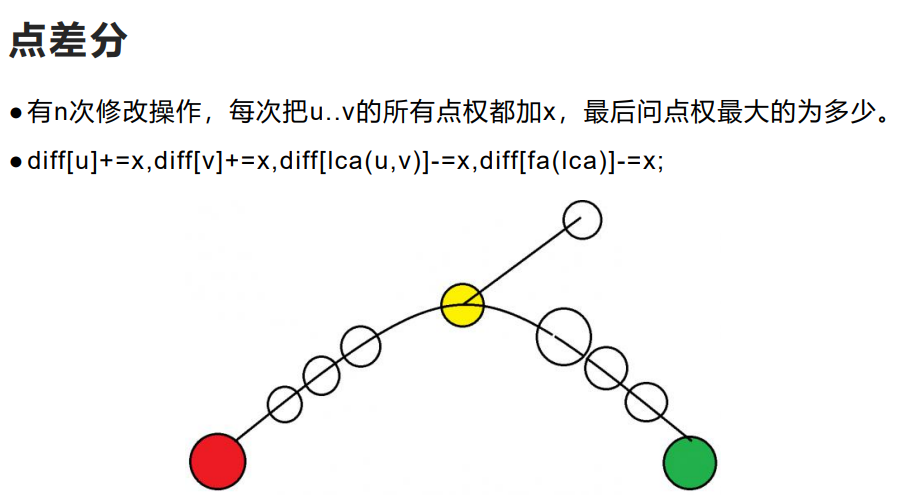
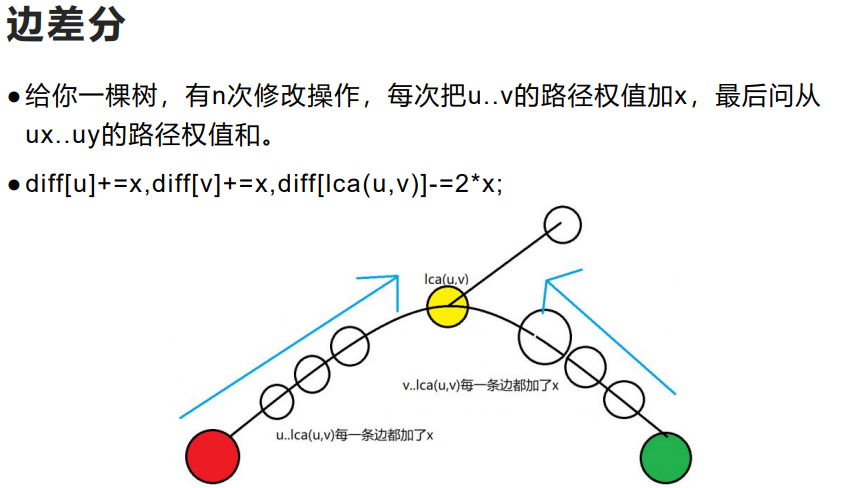
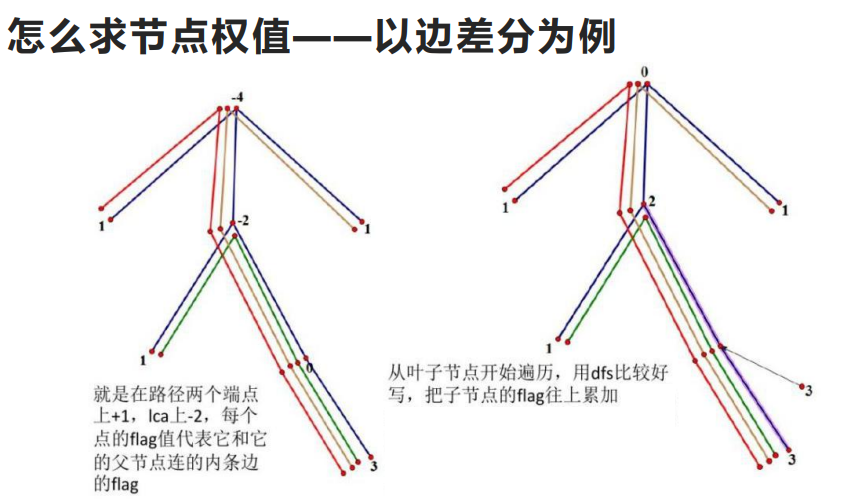
 树上差分

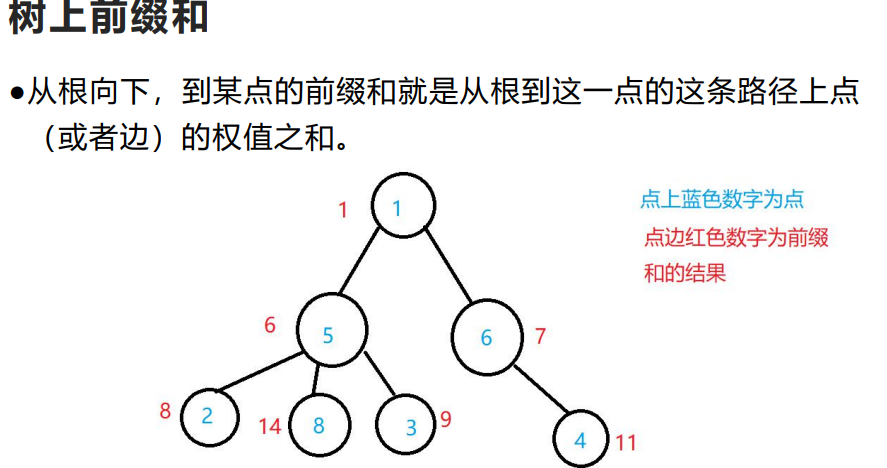
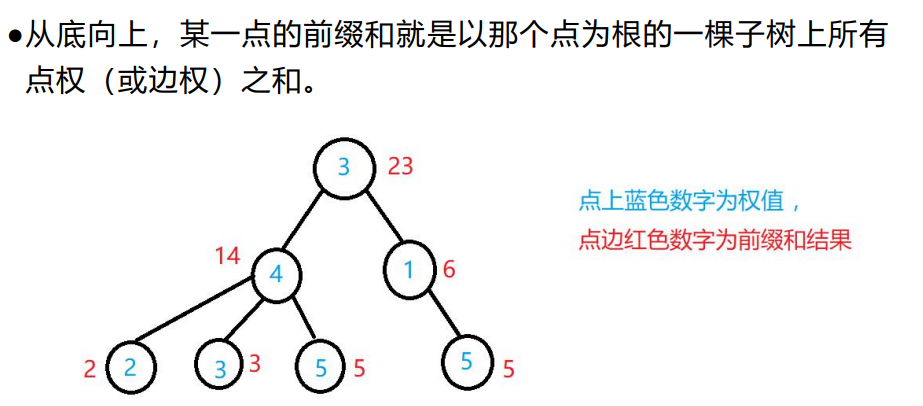
要学树上差分就要先学树上前缀和

 

 

 

 

 

 

 

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> pii;
typedef pair<LL, LL> pll;

const int maxn  = 50000 + 5;
const int maxm  = 100 + 5;
const int inf   = 0x3f3f3f3f;
const LL  mod   = 1e9 + 7;//19260817
const double pi = acos(-1.0);

int n, m, x, y, cnt, ans, LCA, c[maxn], deep[maxn], pre[maxn][21], head[maxn];

struct node{
    int to, next;
}edge[maxn << 1];

void addedge(int u, int v){
    edge[++cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt;
}

void dfs(int x, int f){
    pre[x][0] = f;
    for(int i = head[x]; i; i = edge[i].next){
        if(edge[i].to != f){
            deep[edge[i].to] = deep[x] + 1;
            dfs(edge[i].to, x);
        }
    }
}

void solve(){ 
    for(int j = 1; j <= 18; j++)
        for(int i = 1; i <= n; i++)
            pre[i][j] = pre[pre[i][j - 1]][j - 1];
}

int lca(int u, int v){
    if(deep[u] < deep[v]) swap(u, v);
    int dc = deep[u] - deep[v];
    for(int i = 0; i <= 18; i++){
        if((1 << i) & dc) u = pre[u][i];
    }
    if(u == v) return u;
    for(int i = 18; ~i; i--){
        if(pre[u][i] != pre[v][i]){
            u = pre[u][i];
            v = pre[v][i];
        }
    }
    return pre[u][0]; 
}

void dfs1(int x, int f){
    for(int i = head[x]; i; i = edge[i].next) if(edge[i].to != f){
        dfs1(edge[i].to, x);
        c[x] += c[edge[i].to];
        ans = max(ans, c[x]);
    }
}

int main(){
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n - 1; i++){
        scanf("%d %d", &x, &y);
        addedge(x, y), addedge(y, x);
    }
    dfs(1, -1);
    solve();
    for(int i = 1; i <= m; i++){
        scanf("%d %d", &x, &y);
        LCA = lca(x, y);
        c[x]++, c[y]++, c[LCA]--, c[pre[LCA][0]]--;
    }
    dfs1(1, -1);
    printf("%d\n", ans);
    return 0;
}

 

 

 

树链剖分

 

 

 

 

 

 

 

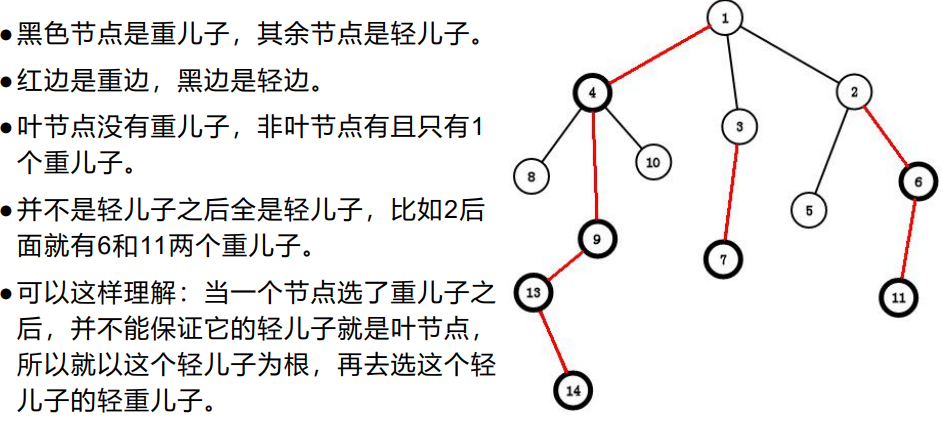
 作用

 

 

 

 

 

 例26. P3384 【模板】轻重链剖分/树链剖分

#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;i<b;i++)
#define mid int m = l+r>>1
#define lson rt<<1,l,m
#define rson rt<<1|1,m+1,r
#define tl tree[rt<<1]
#define tr tree[rt<<1|1]
 
const int N = 1e5+5;
 
int top[N],fa[N],id[N],son[N],dep[N],size[N];
ll w[N],a[N];
 
int n,m,root;
ll mod;
 
struct node {
    int to,last;
}edge[N<<1];
int head[N],idx;
 
ll tree[N<<2],lazy[N<<2];
 
void add(int u,int v){edge[idx].to = v;edge[idx].last = head[u]; head[u] = idx++;}
 
void dfs1(int now,int f,int nowdep){///处理轻重儿子
    dep[now] = nowdep;
    fa[now] = f;
    size[now] = 1;
    for (int i=head[now];i!=0;i=edge[i].last){
        int v = edge[i].to;
        if (v==f) continue;
        dfs1(v,now,nowdep+1);
        size[now] += size[v];
        if (size[v] > size[son[now]]) son[now] = v;
    }
}
 
int tot;
void dfs2(int now,int topf){///处理轻重边
    id[now] = tot++;
    a[id[now]] = w[now]%mod;
    top[now] = topf;
    if (!son[now]) return ;//因为没有重儿子意味着没有儿子
    dfs2(son[now],topf);
    for (int i=head[now];i!=0;i=edge[i].last){
        int v = edge[i].to;
        if (v==fa[now] || v==son[now]) continue;
        dfs2(v,v);
    }
}
 
void push_up(int rt){
    tree[rt] = (tl + tr)%mod;
}
 
void push_down(int rt,int len){
    if (rt<0) return ;
    tl = (tl + lazy[rt]*(len-len/2)%mod)%mod;
    tr = (tr + lazy[rt]*(len/2)%mod)%mod;
    lazy[rt<<1] = (lazy[rt<<1] + lazy[rt])%mod;
    lazy[rt<<1|1] = (lazy[rt<<1|1] + lazy[rt])%mod;
    lazy[rt] = 0;
}
 
void update(int L,int R,ll x,int rt,int l,int r){
    if (L<=l && r<=R){
        lazy[rt] = (lazy[rt] + x)%mod;
        tree[rt] = (tree[rt] + x*(r-l+1)%mod)%mod;
        return ;
    }
    if (lazy[rt]) push_down(rt,r-l+1);
    mid;
    if (L<=m) update(L,R,x,lson);
    if (R>m)  update(L,R,x,rson);
    push_up(rt);
}
 
ll query(int L,int R,int rt,int l,int r){
    if (L<=l && r<=R){
        return tree[rt];
    }
    if (lazy[rt]) push_down(rt,r-l+1);
    mid;
    ll ans = 0;
    if (L<=m) ans = (ans + query(L,R,lson))%mod;
    if (R>m)  ans = (ans + query(L,R,rson))%mod;
    return ans;
}
 
void build(int rt,int l,int r){
    if (l==r){
        tree[rt] = a[l];
        return ;
    }
    mid;
    build(lson);
    build(rson);
    push_up(rt);
}
 
ll interval(int x,int y,ll v,int op){
    ll ans = 0;
    while (top[x] != top[y]){
        if (dep[top[x]]<dep[top[y]]) swap(x,y);
        //printf("we deal[%d,%d]\n",id[top[x]],id[x]);
        if (op==1) update(id[top[x]],id[x],v,1,1,n);
        if (op==2) ans = (ans + query(id[top[x]],id[x],1,1,n))%mod;
        x = fa[top[x]];
    }
    if (dep[x]<dep[y]) swap(x,y);
    //printf("we deal[%d,%d]\n",id[y],id[x]);
    if (op==1) update(id[y],id[x],v,1,1,n);
    if (op==2) ans = (ans + query(id[y],id[x],1,1,n))%mod;
    return ans;
}
 
int main()
{
    scanf("%d %d %d %lld",&n,&m,&root,&mod);
    for1(i,1,n) scanf("%lld",w+i);
    int u,v;
    idx = 1;
    for1(i,1,n-1) scanf("%d %d",&u,&v),add(u,v),add(v,u);
    dfs1(root,0,1);
    tot = 1;
    dfs2(root,root);
/*
    for (int i=1;i<=n;i++){
        printf("NO %d：top=%d fa=%d id=%d son=%d dep=%d size=%d\n",i,top[i],fa[i],id[i],son[i],dep[i],size[i]);
    }
*/
    build(1,1,n);
    ll val;
    int op,x,y;
    while (m--){
        scanf("%d",&op);
        if (op==1){
            scanf("%d %d %lld",&x,&y,&val);
            interval(x,y,val,op);
        }
        if (op==2){
            scanf("%d %d",&x,&y);
            printf("%lld\n",interval(x,y,0,op));
        }
        if (op==3){
            scanf("%d %lld",&x,&val);
            //printf("we update[%d,%d]\n",id[x],id[x]+size[x]-1);
            update(id[x],id[x]+size[x]-1,val,1,1,n);
        }
        if (op==4){
            scanf("%d",&x);
            //printf("we query[%d,%d]\n",id[x],id[x]+size[x]-1);
            printf("%lld\n",query(id[x],id[x]+size[x]-1,1,1,n));
        }
    }
    return 0;
}

 

 

 

 

 

// 注意， 以一个点 x 为顶端的链的长度为 treedep[x]-dep[x]+1;
// 由于这个 sb 错误我调了很久qwq
// 希望看这篇博文的人引以为戒 qwq
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5+15;

#define ui unsigned int
ui s;
inline ui get(ui x) {
    x ^= x << 13;
    x ^= x >> 17;
    x ^= x << 5;
    return s = x; 
}

int n,q,rt;
vector<int>e[maxn],ks[maxn],kf[maxn];
int treedep[maxn],dep[maxn],son[maxn],top[maxn];
int f[21][maxn];

void po1(int x,int fa,int Dep) {
    treedep[x]=dep[x]=Dep;
    f[0][x]=fa;
    for(int i=0;i<(int)e[x].size();++i) {
        int y=e[x][i]; if(y==fa) continue;
        po1(y,x,Dep+1);
        if(treedep[y]>treedep[son[x]]) treedep[x]=treedep[son[x]=y];
    }
}
void po2(int x,int tp) {
    top[x]=tp;
    if(son[x]) po2(son[x],tp);
    for(int i=0;i<(int)e[x].size();++i) {
        int y=e[x][i]; if(y==f[0][x]||y==son[x]) continue;
        po2(y,y);
    }
}

int highbit[maxn];
int kfa(int x,int k) {
    if(!k) return x;
    int r=highbit[k];
    x=f[r][x];
    k-=(1<<r);
    if(dep[x]-k<dep[top[x]])
        return kf[top[x]][dep[top[x]]-(dep[x]-k)];
    else
        return ks[top[x]][(dep[x]-k)-dep[top[x]]];
}

int ans[5000005];
int main()
{
    cin>>n>>q>>s;
    for(int i=1;i<=n;++i) {
        int ff;scanf("%d",&ff);
        if(ff) e[ff].push_back(i);
        else rt=i;
    }
    po1(rt,0,1);
    po2(rt,rt);
    for(int k=1;k<=20;++k)
        for(int i=1;i<=n;++i)
            f[k][i] = f[k-1][f[k-1][i]];
    for(int x=1;x<=n;++x) if(x==top[x]) {
        int ns=x, nf=x;
        for(int i=0;i<=treedep[x]-dep[x]+1;++i) {
            ks[x].push_back(ns), kf[x].push_back(nf);
            ns=son[ns], nf=f[0][nf];
        }
    }
    for(int i=1;i<=n;++i) highbit[i] = log2(i);
    for(int i=1;i<=q;++i) {
        int x=((get(s) xor ans[i-1]) % n)+1;
        int k=(get(s) xor ans[i-1])%dep[x];
        ans[i] = kfa(x,k);
    }
    long long ANS = 0ll;
    for(int i=1;i<=q;++i) ANS ^= 1ll*i*ans[i];
    cout << ANS;
    return 0;
}