【ICPC 2020上海区域赛】Traveling in the Grid World（平面几何）

题面

如果此时 $n,m\le 10^{18}$ 怎么办呢？

题解

题意都明白吧，从 $A(0,0)$ 到 $B(n,m)$ 连一条由线段组成的折线路径，要求如题。

如果 $n,m$ 互质的话，直接欧几里得距离就行了，

那要是不互质呢？就不能一条线段连过去了

我们可以证明，最多两条线段，是可以连过去的，最优的答案一定中间只有一个折点。

---

我们用调整法证明两个推论：

1. 任意一个两条线段组成的折线路径，如果非端点的部分经过了整点，则一定可以调整为一条更优的路径。
2. 如果存在一条超过两条线段的折线路径，一定能调整为一个更优的两条线段组成的路径。

首先证明第一条，如图，这是一条不合法的折线，上面有个整点为 C：

很直观地，我们把 B 和 C 相连，那么 $A\to C\to B$ 比 $A\to M\to B$ 更优，

因为 $△BCM$ 内两边之和大于第三边。
如果此时AC或者BC上还有一个整点D，那么就重复上述过程，一定最终会得到一条合法路径，且一次比一次更优。

我们再证明第二个推论，如图是一条挺曲折的路径（由折线组成）：

由于它是折线，所以一定存在一个中间的端点 C，满足 $A,B,C$ 三点不共线（这个应该不用证了吧，稍微反推一下就好），然后把 C 分别连向 A 和 B，由于两点之间线段最短，所以 $A\to C\to B$ 一定更优。此时若不合法，再通过上文的第一条推论调整即可。

---

好，那么我们明确了答案一定为两条线段了，接下来我们通过这一点来做：

最优答案一定在离 AB 最近的、有格点的、与 AB 平行的直线上

（自我感觉这挺显然的，并且国集爷讲到这儿时觉得过于显然跳过了，虽然这很正常，但是放开想一下会感觉有反例，如果不严谨证明一下是不行的。看官们可以在这里找一下证明，笔者真不会证🙉，谅解一下谢谢）

怎么找这样一个点呢？ 因为直线与AB平行，所以它一定在这样一条线上：

$y=\frac{m}{n}x+c$ ，其中在有整点的前提下，c 要最小，

我们把它先约分一下，
令 $N=\frac{n}{gca(n,m)},M=\frac{m}{gcd(n,m)}$,
则可以变成 $y=\frac{M}{N}x+c,(N,M互质)$

再变一下式：
$$\begin{gathered} Ny=Mx+Nc \\ Ny-Mx=Nc \\ N(y)+M(-x)=Nc \end{gathered}$$
我们知道，这样一个不定方程有整数解当且仅当 $Nc$ 是 $gcd(N,M)=1$ 的倍数，由于 c 可以是任意实数（我们并没说过 c 一定是整数吧），所以 c 最小可以是 $\frac{1}{N}$ ，这时 $Nc=1$，方程的特解可以由扩展欧几里得算法得出，假设特解为$(x^{\prime },y^{\prime })$，那么通解为
$(x,y)=(x^{\prime },y^{\prime })+k\cdot (N,M)$

然后，就是一个简单的初中几何题了

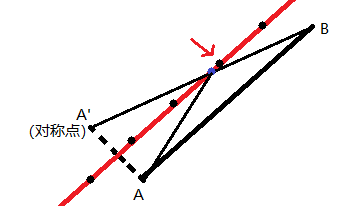
（经典老对称）只用找距离 A’B 和 $y=\frac{M}{N}x+c$ 的交点最近的那个格点，这个可以三分，也可以暴力数学推导O(1)做。

所以这道题， $n,m\le 10^{18}$ 也不怕，一样可以 $O(Tlogn)$ 解决。

CODE

（笔者为了节省时间就只打了个exgcd暴力应付这道题，供对拍用，大家有兴趣可以尝试 $O(Tlogn)$ 的解法）

#include<map>
#include<ctime>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1005
#define LL long long
#define ULL unsigned long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) ((-(x)) & (x))
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return x * f;
}
const int MOD = 1000000007;
int n,m,i,j,s,o,k;
int exgcd(int a,int b,int &x,int &y) {
	if(b == 0) {x=1;y=0;return a;}
	int r = exgcd(b,a % b,y,x);
	y -= x*(a/b); return r;
}
DB dis(int x,int y,int a,int b) {
	return sqrt((DB)(x-a)*1.0*(x-a) + (y-b)*1.0*(y-b));
}
int main() {
	int T = read();
	while(T --) {
		n = read();m = read();
		int x,y,N,M;
		int gc = exgcd(n,m,y,x); x = -x;
		if(gc == 1) {
			printf("%.10f\n",dis(0,0,n,m));
			continue;
		}
		N = n/gc;M = m/gc;
		while(x > 0 && y > 0) x -= N,y -= M;
		while(x < 0 || y < 0) x += N,y += M;
		DB ans = 1e18;
		while(x < n && y < m) {
			ans = min(ans,dis(0,0,x,y) + dis(x,y,n,m));
			x += N;y += M;
		}
		printf("%.10f\n",ans);
	}
	return 0;
}