差点被转卖的乘法表

源自_{数 据 删 除}出的套题，挺有意思的。题目与 ??? 来源相同。

题目

柯伊伯带，落难的外星飞船，

除了那些胶皮一样的外星人日记，工作人员还发现了一张画着奇怪符号矩阵的画，经过充分的观察，认定这是一张乘法表，

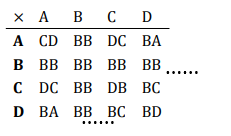
虽然这个长着倒三角头和人类身形的外星人双手共有 10 根手指，应该用的也是十进制数，但是这张乘法表却是 $p$ 进制的，因为它共有 $p$ 种不同的符号。这并不奇怪，人类也是用的十进制，但计算机要发展还是得有二进制、八进制和十六进制。

乘法表上第 $i$ 行第 $j$ 列是一个两位数 $A_{i,j}p+B_{i,j}$（$A$ 可以是 0），表示符号 $i$ 与符号 $j$ 相乘的结果，其中 $A,B$ 也是两个符号。由于符号过多，这里用 $0,1,2,3...$ 等数字编号代替符号，每个符号唯一对应一个 $0\sim p-1$ 之间的数。

现在给出这个乘法表，要求破译出每个符号代表的数。朴素乘法是不会受虫洞干扰的，所以这个乘法表一定有唯一解。把乘法表破译后，古河打算把它高价卖给数学收藏家。

$p\le 2000$ .

Solution

想法很妙啊，

首先，我们会发现，如果 $x$ 代表的是 0 的话，那么第 $x$ 行和第 $x$ 列肯定全是“$xx$”（$xp+x$），这样的符号只能有一个，所以我们找到了 0 。

然后，通过对十进制乘法表的观察，我们不难发现一个惊人的结论：数字 $x$（$x>0$） 所在的行/列出现的所有数的第二位，一定只会出现 $0\sim x-1$ ，而且这里面每个数都一定出现，也就是说，它所在的行本质不同的第二位符号数一定刚好是 $x$ 。

所以，我们统计每一行第二位数字（符号）本质不同的有多少个，就可以求出该行符号代表的数了。

时间复杂度 $O(p^2)$ ，万万没想到只是遍历的复杂度。

CODE

出题人的 std ，猜猜这是谁

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#include <map>

#define N 4005
#define M 15
#define mod 1000000007
#define mod2 100000000
#define ll long long
#define maxi(a,b) (a)>(b)? (a) : (b)
#define mini(a,b) (a)<(b)? (a) : (b)

using namespace std;

int cnt;
int p;
int i, j;
int a[N][N];
int c[N][N];
int cc[N];
int ans[N], pp[N];

int main() {
//	freopen("--------------.in", "r", stdin);
//	freopen("--------------.out", "w", stdout);
	cnt = 1;
	scanf("%d", &p);
	for (i = 0; i < p; i++) {
		for (j = 1; j <= p; j++) {
			scanf("%d", &a[i][2 * j - 1]);
			cc[ a[i][2 * j - 1] ]++;
			scanf("%d", &a[i][2 * j]);
			cc[ a[i][2 * j] ]++;
		}
	}

	int ma = cc[0];
	int index = 0;
	for (i = 0; i < p; i++) {
		if (cc[i] > ma) {
			ma = cc[i];
			index = i;
		}
	}
	ans[0] = index;

	memset(cc, 0, sizeof(cc));

	for (i = 0; i < p; i++) {
		for (j = 1; j <= p; j++) {
			if (c[i][ a[i][2 * j - 1] ] == 0) {
				c[i][ a[i][2 * j - 1] ] = 1;
				cc[i]++;
			}
		}
		if (cc[i] == 1) {
			if (ans[0] != i)
				ans[1] = i;
		} else {
			ans[ cc[i] ] = i;
		}
	}
	for (int i = 0; i < p; i++)
		pp[ans[i]] = i;
	for (i = 0; i < p; i++)
		printf("%d%c", pp[i], " \n"[i == p - 1]);
}