CF1442D Sum （动态规划，线段树分治）

${}_{{}_{（宋体字看起来真舒服）}}$

$题{面}_{{}_{(洛谷翻译)}}$

给定$n$个不降的数组。
有一个值$ans$，初始为$0$
你需要进行如下操作$k$次：

1.选择一个数组
2.把$ans$加上数组的第一个元素。
3.把数组的第一个元素删除。

请求出$ans$最大是多少。

所有数组的元素总个数$\le 10^6,n,k\le 3000$

$输{入}_{{}_{(笔者亲自翻译)}}$

第一行包含两个整数 $n$ and $k$ ( $1\le n,k\le 3000$ ): 分别是数组和操作的数量。

接下来的 $n$ 行每一行包含一个数组。 每一行的第一个整数是 $t_i$ ( $1\le t_i\le 10^6$ ): 第 $i$ 个数组的大小。 后面 $t_i$ 个整数 $a_{i,j}$ ( $0\le a_{i,1}\le \dots \le a_{i,t_i}\le 10^8$ ) 给出了第 $i$ 个数组。

保证 $k\le \sum _{i=1}^n{t}_i\le 10^6$。

$样例$

$input$

3 3
2 5 10
3 1 2 3
2 1 20

$output$

26

$题解$

转换一下模型，相当于一个背包问题，这个不用我多说了吧。

我们会发现一个结论：最后的最优操作一定是把一些数组全选完，最多一个数组只选部分。

$Step1证明结论$

我们要证这个结论，实际上要证最优操作不存在两个只选了部分的数组：

为了方便证明，我们定义两个数组总和相等的时候，两数组选的数量相差更大的更优

其实很简单，如果存在这么两个数组选了部分：

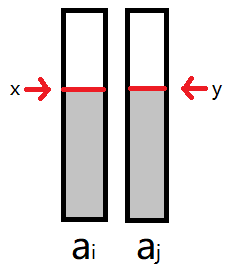
那么以下两种情况肯定更优：

1. $a_{i,x}\ge a_{j,y}\Rightarrow a_{i,x+1}\ge a_{j,y}:$
   
2. $a_{i,x}\le a_{j,y}\Rightarrow a_{j,y+1}\ge a_{i,x}:$
   

而这两种情况已经包含全集了（$a_{i,x}\ge a_{j,y}$ 和 $a_{i,x}\le a_{j,y}$），所以充分证明了 两个数组都没选完，在中间稳定 的情况是不存在的，因此最多就只有其中一个选完了，另一个没选完的情况。

$Step2利用结论$

这个结论怎么利用呢？

相当于我们如果确定某一个数组是只选部分的那一个，那么其他的数组就降维了、变成一个数了、一个物品了！

于是我们可以先把其他数组假设成只有一个数，然后把背包跑出来，最后暴力枚举只选部分的那个数组具体选几个。

那么，每一个数组一开始都有一个空的背包dp数组，表示该数组只选部分的情况下其他数组放进来处理的背包。但是这样还是 $O(n^{2}k)$ 的过不了。

我们可以想想怎么优化。我们发现每个数组 $i$ 整个考虑会对 $[1,i-1]\cup [i+1,n]$ 内的其他数组的背包有贡献，这是两个区间，因此我们可以用线段树分治优化它，

这样一来每个数组就要对 $logn$ 个区间有贡献，而每次贡献是一次 $O(m)$ 的背包更新，时间复杂度 $O(nmlogn)$。

最后，由于每个数组挂的区间有特殊性，可以不用真的建一棵线段树，直接判断挂在当前区间的数组有哪些就行了。

$CODE$

#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 3005
#define LL long long
#define DB double
#define ENDL putchar('\n')//#define lowbit(x) ((-x)&(x))
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return f * x;
}
const int MOD = 998244353;
int n,m,i,j,s,o,k,sq;
LL dp[100][MAXN];
bool f[100][MAXN];
vector<LL> a[MAXN];
int b[MAXN];
LL ans = 0;
void solve(int l,int r,int de) {
	memcpy(dp[de],dp[de-1],sizeof(dp[de]));
	memcpy(f[de],f[de-1],sizeof(f[de]));
	for(int i = 1;i <= n;i ++) {
		if(i == l) {
			i = r;continue;
		}
		if(!f[de][i]) {
			f[de][i] = 1;
			int tp = a[i][0];
			for(int j = m;j >= tp;j --) {
				dp[de][j] = max(dp[de][j],dp[de][j-tp] + a[i][tp]);
			}
		}
	}
	if(l < r) {
		int mid = (l + r) >> 1;
		solve(l,mid,de+1);solve(mid+1,r,de+1);
		return ;
	}
	else {
		int tp = a[l][0];
		ans = max(ans,dp[de][m]);
		for(int i = 1;i <= tp && i <= m;i ++) {
			ans = max(ans,dp[de][m-i] + a[l][i]);
		}
	}
	return ;
}
int main() {
	n = read();m = read();
	for(int i = 1;i <= n;i ++) {
		s = read();
		LL sm = 0;
		a[i].push_back(s);
		while(s --) {
			sm += read();
			a[i].push_back(sm);
		}
	}
	solve(1,n,1);
	printf("%lld\n",ans);
	return 0;
}