JOIOI王国 - 二分+贪心

题面

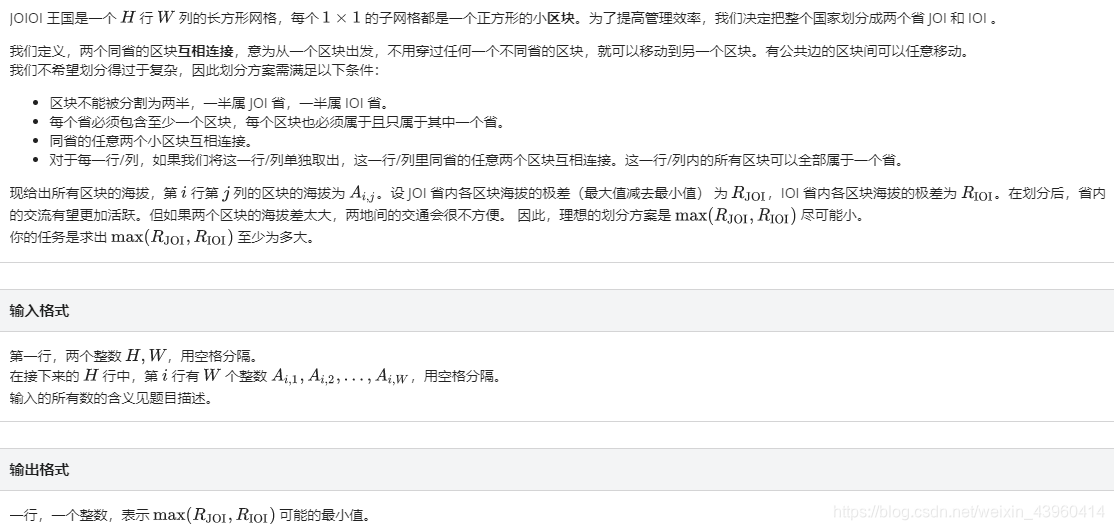
题解

通过一句经典的话“最大值的最小值” 我判断它是二分题，

不难发现，整个图形中两个省的分界线是一条单调不递减或单调不递增的折线。

而且，越到后来它的最大值只会越来越大，最小值只会越来越小，极差只会越来越大。

所以如果我们把ans上界定下来了，我们就可以贪心的让它其中一个区域的值在 [maxa - ans , maxa] 的灰色地带发展，然后判断另一个区域是否合法。由于另一个区域的点数越少越好，所以在灰色地带要尽量发展得广。

我们只能先定义一个 p 表示当前行两省的分界, 然后在第一行尽量扩展得远，下一行在 [0 , p]之间扩展得远，这样不仅可以让另一个区域的点更少，而且可以让下一行有更大的发展空间。

其它的贪心方法就不行了，所以分别行数从小到大和从大到小各枚举一次，然后做个左右对称再来。

CODE

#include<cstdio> 
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#define LL long long
using namespace std;
inline LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
	while(s >= '0' && s <= '9'){x = x * 10 + s - '0';s = getchar();}
	return x * f;
}
LL n,m,i,j,s,o,k,flag = 0;
LL a[2005][2005];
int b[2005],c[2005];
int x1 = 1,x2 = 1,y1 = 1,y2 = 1;
LL maxl[2005][2005];
LL maxr[2005][2005];
LL minl[2005][2005];
LL minr[2005][2005];
LL ans = 1e18;
bool check(LL mid) {
	LL minn = a[x1][y1] - mid;
//	cout<<minn<<endl;
	LL p = m,mi1 = 0x7f7f7f7f,mi2 = 0x7f7f7f7f,ma1=0,ma2=0;
	for(int i = 1;i <= n;i ++) {
		int pp = p;
		for(int j = 0;j <= pp;j ++) {
			if(minl[i][j] >= minn) {
				p = j;
			}
		}
		mi1 = min(mi1,minl[i][p]);
		ma1 = max(ma1,maxl[i][p]);
		mi2 = min(mi2,minr[i][p + 1]);
		ma2 = max(ma2,maxr[i][p + 1]);
	}
//	cout<<"ok1"<<endl;
	if(max(ma1 - mi1,ma2 - mi2) <= mid) return 1;
	p = m,mi1 = 0x7f7f7f7f,mi2 = 0x7f7f7f7f,ma1=0,ma2=0;
	for(int i = n;i > 0;i --) {
		int pp = p;
		for(int j = 0;j <= pp;j ++) {
			if(minl[i][j] >= minn) {
				p = j;
			}
		}
		mi1 = min(mi1,minl[i][p]);
		ma1 = max(ma1,maxl[i][p]);
		mi2 = min(mi2,minr[i][p + 1]);
		ma2 = max(ma2,maxr[i][p + 1]);
	}
//	cout<<"ok2"<<endl;
	if(max(ma1 - mi1,ma2 - mi2) <= mid) return 1;
	p = 0,mi1 = 0x7f7f7f7f,mi2 = 0x7f7f7f7f,ma1=0,ma2=0;
	for(int i = 1;i <= n;i ++) {
		int pp = p;
		for(int j = m;j >= pp;j --) {
			if(minr[i][j + 1] >= minn) {
				p = j;
			}
		}
		mi1 = min(mi1,minl[i][p]);
		ma1 = max(ma1,maxl[i][p]);
		mi2 = min(mi2,minr[i][p + 1]);
		ma2 = max(ma2,maxr[i][p + 1]);
	}
//	cout<<"ok3"<<endl;
	if(max(ma1 - mi1,ma2 - mi2) <= mid) return 1;
	p = 0,mi1 = 0x7f7f7f7f,mi2 = 0x7f7f7f7f,ma1=0,ma2=0;
	for(int i = n;i > 0;i --) {
		int pp = p;
		for(int j = m;j >= pp;j --) {
			if(minr[i][j + 1] >= minn) {
				p = j;
			}
		}
//		printf("p---%d\n",p);
		mi1 = min(mi1,minl[i][p]);
		ma1 = max(ma1,maxl[i][p]);
		mi2 = min(mi2,minr[i][p + 1]);
		ma2 = max(ma2,maxr[i][p + 1]);
	}
//	cout<<"ok4"<<endl;
	if(max(ma1 - mi1,ma2 - mi2) <= mid) return 1;
	return 0;
}
LL solve(LL l,LL r) {
//	printf("%lld %lld\n",l,r);
	if(l >= r - 1) {
		if(check(l)) return l;
		return r;
	}
	LL mid = (l + r) / 2;
	if(check(mid)) return solve(l,mid);
	return solve(mid,r);
}
int main() {
	n = read();m = read();
	for(int i = 1;i <= n;i ++) {
		minl[i][0] = 1e18;
		for(int j = 1;j <= m;j ++) {
			a[i][j] = read();
			if(a[i][j] > a[x1][y1]) x1 = i,y1 = j;
			if(a[i][j] < a[x2][y2]) x2 = i,y2 = j;
			minl[i][j] = min(minl[i][j - 1],a[i][j]);
			maxl[i][j] = max(maxl[i][j - 1],a[i][j]);
		}
		minr[i][m + 1] = 1e18;
		for(int j = m;j > 0;j --) {
			minr[i][j] = min(minr[i][j + 1],a[i][j]);
			maxr[i][j] = max(maxr[i][j + 1],a[i][j]);
		}
//		for(int j = 1;j <= m;j ++) {
//			printf("%lld ",minr[i][j]);
//		}putchar('\n');
	}
	printf("%lld\n",solve(0,a[x1][y1] - a[x2][y2]));
	return 0;
}