七月数据结构题瞎做

P8987 [北大集训 2021] 简单数据结构

如果 \(a\) 初值是 0，那么由于 \(a\) 单调，所有操作都是平凡的，只需要线段树二分+区间推平即可维护。

现在 \(a\) 有初值，然而我们发现全局取 min 会让所有 \(\ge v\) 的数变成 \(v\)，从而使这些数可以用初值为 0 的方式去处理。需要多维护一些东西，比如区间总点数、编号和、最大编号、最大值等。

问题转化为求出每个 \(i\) 被成功取 min 的时刻。考虑二分，检查是否存在 \(j\in[1,mid]\) 使得 \(a_i+i\cdot b_j\ge v_j\)，其中 \(b_j\) 表示第 \(j\) 次操作前全局加的次数。对 \(n\) 个数进行整体二分，将式子转化一下：\(v_j-i\cdot b_j\le a_i\)，将 \((b_j,v_j)\) 视为点，\(i\) 视为斜率 \(k\)，则 \(v_j-i\cdot b_j\) 就是截距，现在就相当于在给定所有点和斜率的情况下求出截距的最小值是否 \(\le a_i\)，直接建出凸包（下凸壳）即可。由于 \(b_j,i\) 都单调，所以这一部分复杂度是 \(O(n)\) 的，注意相同的 \(b_j\) 取 \(v_j\) 最小的那个。

复杂度单 log。

P8990 [北大集训 2021] 小明的树

为了方便将点 \(i\) 重标号为被第 \(i\) 个删掉的点，即重标号后的点满足第 \(i\) 个点第 \(i\) 个被删。这里为了方便，删点轮次从 \(2\) 开始标号。

发现“对于所有白点，它的子树内点都是白点”这个限制非常不好刻画，于是得到了本题的关键性质：“对于所有白点，它的子树内点都是白点”和“所有黑点连通”，两个命题等价。而连通块个数就是点数减边数，线段树维护每次操作过后的黑点数-黑边数 \(B\) 和白点数-白边数 \(W\)，黑白点数平凡的，初始所有边都是黑的，对于一条边 \((x,y),x<y\)，若 \(x=1\)，则 \(y\) 时刻黑边变成杂边，\([y,n],B\leftarrow B+1\)；若 \(x\neq 1\)，则 \(x\) 时刻黑边变杂边，\([x,n],B\leftarrow B+1\)，\(y\) 时刻杂边变白边，\([y,n],W\leftarrow W-1\)。线段树维护 \(B\) 的最小值即该条件下 \(W\) 的和，为了维护这两个信息需额外维护满足在 \(B\) 最小的条件的时刻数量。修改是平凡的。复杂度单 log。

QOJ8240 Card Game

考虑序列的第一个元素，如果序列里存在第二个该元素，那么根据题意，该元素第二次出现位置之前的所有数都该被扔掉，然后转化为规模更小的子问题；否则，该元素一定会被保留下来，然后仍然转化为规模更小的子问题。形式化的来说：

• 设 \(a_i\) 在 \(i\) 之后的下一次出现在 \(nxt_i\)
• \(ans(l,r)=ans(l+1,r)+1\)，若 \(nxt_i>r\)
• \(ans(l,r)=ans(nxt_i+1,r)\)，若 \(nxt_i\le r\)

考虑从右往左扫描线 \(l\)，则对于 \(r\in[l,nxt_l)\)，区间加 1；对于 \(r\in [nxt_l,n]\)，继承 \(l=nxt_l+1\) 的答案。现在要强制在线，可持久化一下就行。复杂度一个 log。

P11343 [KTSC 2023 R1] 出租车旅行

显然，每次到达的点要满足 \(b\) 单调递减，否则不如不换乘。需要特殊处理一下终点的情况，终点没有限制。设 \(f_u\) 表示满足限制到达 \(u\) 的最小代价，转移就是 \(f_v=\min_{b_u>b_v}\{f_u+\text{dist}(u,v)\cdot b_u+a_u\}\)。树上路径问题考虑点分治，假设分治中心为 \(r\)，那么拆一下可以得到 \(f_v=f_u+(\text{dist}(u,r)+\text{dist}(v,r))\cdot b_u+a_u\)，移一下项可得 \(f_u+a_u+\text{dist}(r,u)\cdot b_u=-b_u\cdot \text{dist}(r,v)+f_v\)，将 \((-b_u,f_u+a_u+\text{dist}(r,u)\cdot b_u)\) 视为一个点，\(\text{dist}(r,v)\) 视为斜率，\(f_v\) 视为截距，那么问题转化为给定若干个点和斜率求最小截距，对每个点维护当以该点为分治中心时的下凸壳，注意如果两个点在点分树上的 lca 不为该分治中心，答案必然不优，所以不需要钦定两个点不在同一子树。由于横坐标有单调性所以构造可以线性，但由于斜率没有单调性所以必须凸包上二分。这样做法就明了了：按照 \(b_i\) 倒序枚举 \(i\)，在凸包上二分，并在它的每个点分父亲上插入该点，总共插入 \(O(n\log n)\) 次。而终点的情况直接在所有点插入完毕后再做一遍凸壳上二分即可。复杂度两个 log。

P4220 [WC2018] 通道

弱化：P4565

边分治： 和点分治类似，每次选取一条边，满足该边两边的子树大小差值尽可能小，然后递归下去。直接做复杂度会被卡到平方，但是注意到二叉树的复杂度是正确的，考虑将原树转化为二叉树，并保留原树上的路径信息。有两种做法：一种是类似线段树建树的方式，在两个点之间建一个虚点连接它的两个儿子；一种是直接从前往后或从后往前暴力两两合并，新建节点连接要合并的两个点。注意为了让路径信息正确，新建的点和父亲的边权值为 0，原来的点和父亲的边权值为 1。两种做法的新建点数都不超过 \(n\)，总点数还是 \(O(n)\)，故边分治的复杂度仍然是 \(O(n\log n)\)。

将 \(T_1\) 边分治，分治中心两边的点集为 \(L,R\)，在 \(T_2\) 上对分治点集建立虚树，虚树总点数为 \(O(n\log n)\)，考虑枚举虚树上 LCA，现在要求 \(i\in L,j\in R,dep_1(i)+dep_1(j)+dep_2(i)+dep_2(j)-2dep_2(lca)+dis_3(i,j)\) 的最大值，\(2dep_2(lca)\) 扔出去，剩下的项除了 \(dis_3(i,j)\) 只跟点本身有关。

比较厉害的想法是，在 \(T_3\) 上对每个点建一个虚点，虚点向对应实点连长度为 \(dep_1(i)+dep_2(i)\) 的边，问题转化为求 \(T_3\) 的带限制直径，带限制指的是限制的直径的两个端点的取值。由于边权非负，所以两个点集合并后，新点集的直径端点一定在原点集的直径端点中取到，现在加上了两端颜色不同的限制，一个经典错误做法是指新直径端点一定在原直径端点，如果两个端点颜色相同那么直径大小减掉正无穷。反例：

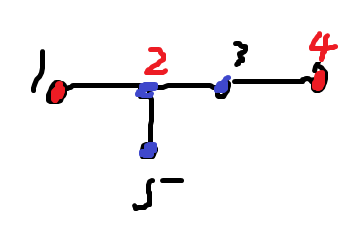
\((2,3)\) 边长为 \(2\)，编号颜色代表的是颜色，节点颜色代表所属集合，现在要把红点和蓝点合并，红点的直径是 \((1,4)\)，蓝点的直径是 \((2,3)\)，而合并后的直径 \((4,5)\) 中的 \(5\) 不属于任何直径的端点。

正确的做法是，维护出子树内不同颜色内部的直径，结论是合并后的直径两端分别来自两个集合的两种颜色内部的直径端点。

总复杂度两个 log，但是我们可以先将点按照 dfn 序排好序然后将边分树拿出来，然后按照 dfn 序依次向边分祖先插入该点，这样就省掉 log 次排序，最终复杂度单 log。