Ybt 金牌导航 6.1.G. 八纵八横 / P3733 [HAOI2017] 八纵八横（线段树分治+线性基）

题意简述

有一个 \(n\) 点 \(m\) 边的无向图以及 \(Q\) 次操作，每次操作会加边、删边、改变边的权值。

在所有操作前和每次操作后，求出以 \(1\) 为起点、以 \(1\) 为终点的路径上边权异或和的最大值。边可以走多次，相应的边权也应当被异或相应多次。

\(n,m\le 500,Q,\log w_i\le 1000\)，所有权值以二进制形式给出。

分析

看到加删操作，如果不能很好的用某个东西支持加入和删除的话，考虑线段树分治，将删除改为撤销，此时修改操作也相当于先删边后加边。

看到异或权值最大，考虑线性基。难点在于如何把路径用线性基中的元素表示出来。

由于异或两次一条边的权值就抵消了，考虑什么样的边会走两次（或者偶数次）。显然，由于最终要回到 \(1\)，所以我们应当以一个包含 \(1\) 的环（这个环可能只包含 \(1\)）为依托，不断向外扩展边。那么，如果一条边不在环上，经这条边出环会走一次，经这条边再回到原来的环再走一次（显然不能从别的边入环，否则这条边就在环上）。而两个环相交的部分也会因为走过两次而被抵消贡献。由此简单证明了只有环上的边才可能有贡献。

那么我们只需要随便拎出一个 dfs 树，对于每个非树边，肯定存在一个由该边和若干条树边构成的环，把这个环的权值扔到线性基里就行。

如何处理包含两个或多个非树边的环呢？我们发现其实这种环一定可以由两个或多个线性基中的环通过异或表示出来，所以不用考虑这种情况。

下图是一个例子。（粗边代表树边，细边代表非树边）

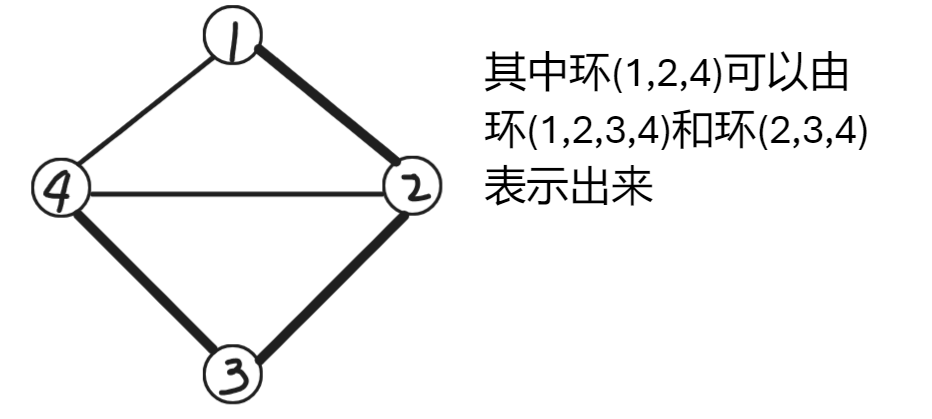
线性基的撤销也很简单，把所有版本的线性基都压到一个栈里（线性基大小为 \(\log w_i\)），撤销时取出栈顶直接覆盖掉原来的即可。

原题中的二进制表示实际上也可以用 bitset 去维护，而众所周知 bitset 有流运算符，故可以使用 cin/cout 读入和输出。当然这题有些写法不能直接输出，需要一些小处理。

时间复杂度为 \(O(\frac{q\log m\log^2 w_i}{w})=O(\text{能过})\)。

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<map>
#include<unordered_map>
#include<vector>
#include<queue>
#include<bitset>
#include<set>
#include<ctime>
#include<random>
#define x1 xx1
#define y1 yy1
#define IOS ios::sync_with_stdio(false)
#define ITIE cin.tie(0);
#define OTIE cout.tie(0);
#define PY puts("Yes")
#define PN puts("No")
#define PW puts("-1")
#define P__ puts("")
#define PU puts("--------------------")
#define popc __builtin_popcount
#define pii pair<int,longint>
#define mp make_pair
#define fi first
#define se second
#define gc getchar
#define pc putchar
#define pb emplace_back
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
#define reprange(a,b,c,d) for(int a=b;a<=c;a+=d)
#define perrange(a,b,c,d) for(int a=b;a>=c;a-=d)
#define graph(i,j,k,l) for(int i=k[j];i;i=l[i].nxt)
#define lowbit(x) (x&-x)
#define lson(x) (x<<1)
#define rson(x) (x<<1|1)
#define mem(x,y) memset(x,y,sizeof x)
#define longint bitset<1005>
//#define double long double
//#define int long long
//#define int __int128
using namespace std;
bool greating(int x,int y){return x>y;}
bool greatingll(long long x,long long y){return x>y;}
bool smallingll(long long x,long long y){return x<y;}
namespace Fread {
	const int SIZE=1<<21;
	char buf[SIZE],*S,*T;
	inline char getc(){if(S==T){T=(S=buf)+fread(buf,1,SIZE,stdin);if(S==T)return '\n';}return *S++;}
}
namespace Fwrite{
	const int SIZE=1<<21;
	char buf[SIZE],*S=buf,*T=buf+SIZE;
	inline void flush(){fwrite(buf,1,S-buf,stdout);S=buf;}
	inline void putc(char c){*S++=c;if(S==T)flush();}
	struct NTR{~NTR(){flush();}}ztr;
}
/*#ifdef ONLINE_JUDGE
#define getchar Fread::getc
#define putchar Fwrite::putc
#endif*/
inline int rd(){
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}
inline void write(int x,char ch='\0'){
	if(x<0){x=-x;putchar('-');}
	int y=0;char z[40];
	while(x||!y){z[y++]=x%10+48;x/=10;}
	while(y--)putchar(z[y]);if(ch!='\0')putchar(ch);
}
inline void write_long(longint x,char ch='\0'){
	bool flag=1;
	per(i,1000,0){if(x[i]==1)flag=0;if(!flag)cout<<x[i];}
	if(flag)cout<<0;if(ch!='\0')cout<<'\n';
}
bool Mbg;
const int maxn=2e3+5,maxm=25,inf=0x3f3f3f3f,L=1000;
const long long llinf=0x3f3f3f3f3f3f3f3f;
int n,m,Q;
vector<pii>G[maxn];
vector<longint>v;
longint dep[maxn],val[maxn];
bool vis[maxn];
bool operator>(longint x,longint y){
	per(i,L,0)if(x[i]!=y[i])return x[i]>y[i];
	return 0;
}
struct linear_basis{
	longint b[maxn];
	void ins(longint x){
		per(i,L,0)if(x[i]){
			if(b[i].none()){b[i]=x;return;}
			x^=b[i];
		}
	}
	longint qry(){
		longint ans(0);
		per(i,L,0){
			longint res=ans^b[i];
			if(res>ans)ans=res;
		}
		return ans;
	}
}sta[maxm];
int tp;
void dfs(int x,int y){
	vis[x]=1;
	for(pii i:G[x]){
		int u=i.fi;longint w=i.se;
		if(!vis[u])dep[u]=dep[x]^w,dfs(u,x);
		else v.pb(dep[u]^dep[x]^w);
	}
}
vector<longint>d[maxn<<2];
longint ans[maxn];
void upd(int ll,int rr,longint x,int l=1,int r=Q,int p=1){
	if(ll>rr)return;
	if(ll<=l&&r<=rr)return (void)d[p].pb(x);
	int mid=l+r>>1;
	if(ll<=mid)upd(ll,rr,x,l,mid,lson(p));
	if(rr>mid)upd(ll,rr,x,mid+1,r,rson(p));
}
void qry(int l,int r,int p){
	++tp,sta[tp]=sta[tp-1];
	for(longint i:d[p])sta[tp].ins(i);
	if(l==r){ans[l]=sta[tp].qry(),tp--;return;}
	int mid=l+r>>1;qry(l,mid,lson(p)),qry(mid+1,r,rson(p));
	--tp;
}
int lst[maxn],cnt;
int U[maxn],V[maxn];
void solve_the_problem(){
	cin>>n>>m>>Q;
	rep(i,1,m){
		int x,y;longint z;cin>>x>>y>>z;
		G[x].pb(mp(y,z)),G[y].pb(mp(x,z));
	}
	dfs(1,0);
	for(longint i:v)sta[0].ins(i);
	write_long(sta[0].qry(),10);
	if(!Q)return;
	rep(i,1,Q){
		string op;int x,y;longint z;
		cin>>op>>x;
		if(op=="Add"){
			cin>>y>>z;U[++cnt]=x,V[cnt]=y;
			lst[cnt]=i,val[cnt]=dep[x]^dep[y]^z;
		}else if(op=="Cancel"){
			upd(lst[x],i-1,val[x]);
			lst[x]=-1;
		}else{
			cin>>z;
			upd(lst[x],i-1,val[x]);
			lst[x]=i,val[x]=dep[U[x]]^dep[V[x]]^z;
		}
	}
	rep(i,1,cnt)if(lst[i]!=-1)upd(lst[i],Q,val[i]);
	qry(1,Q,1);
	rep(i,1,Q)write_long(ans[i],10);
}
bool Med;
signed main(){
//	freopen(".in","r",stdin);freopen(".out","w",stdout);
//	fprintf(stderr,"%.3lfMB\n",(&Mbg-&Med)/1048576.0);
	IOS;int _=1;while(_--)solve_the_problem();
}
/*

*/