计算机组成与设计 第三章：算术的运算（无浮点数）

@

目录

• 计算机组成与设计 第三章：算术的运算
  • 1.加法和减法
  • 2.乘法器
  • 3.除法器
  • 3.浮点数
    • 浮点数加法

计算机组成与设计 第三章：算术的运算

1.加法和减法

有符号数

对于二进制补码，什么时候发生溢出？
硬件规模总是有一定限制的，例如字宽只有32位。当运算超过这个限制，就会发生溢出。
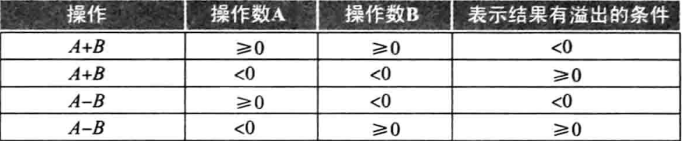
首先看什么时候不会溢出。加法：当相加的两个源操作数符号相异时，不会发生溢出，因为二者的和必定不会大于其中的某一个操作数。若源操作数可以用32位表示，那么这个结果也必然可以用32位表示。减法规则相反，当源操作数符号相同时，不会溢出。例如 c - a可以视为 c + (-a),此时与加法不会溢出时情况相同。
何时发生溢出？当加法和减法之后的结果需要使用多余32位表示时会发生溢出。例如，如果两个正数相加但结果是负数，或者一个负数减去一个正数结果为正数，那么必然发生了溢出。
加减法发生溢出的条件：

无法符号数

无符号数通常用来表示内存地址，这种情况下溢出是可以忽略的

在MIPS中采用两种类型的算术指令来解决问题

• 加法\(\text{(add)}\),立即数加法\(\text{(addi)}\)和减法\(\text{(sub)}\),这三条指令在溢出的时产生异常
• 无符号\(\text{(addu)}\),立即数无符号加法\(\text{(addiu)}\)和无符号减法\(\text{(subu)}\),这三条指令是不会产生异常

异常处理：

• 保存PC指针到异常程序计数器\(\text{(EPC，exception program counter)}\) 的寄存器-

• 跳转到预定义的异常处理地址

• \(\text{mfc0 (move from coprocessor reg)}\) 指令可以取回\(EPC\) 值， 恢复\(PC\)指针。

2.乘法器

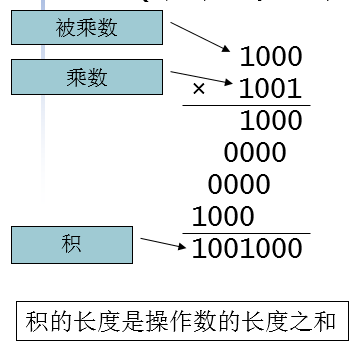
乘数的每一位：\(3\)步，\(3\)个时钟周期

\(32\)位乘数，共\(32 \times 3 = 96\)步，近\(100\)个时钟周期

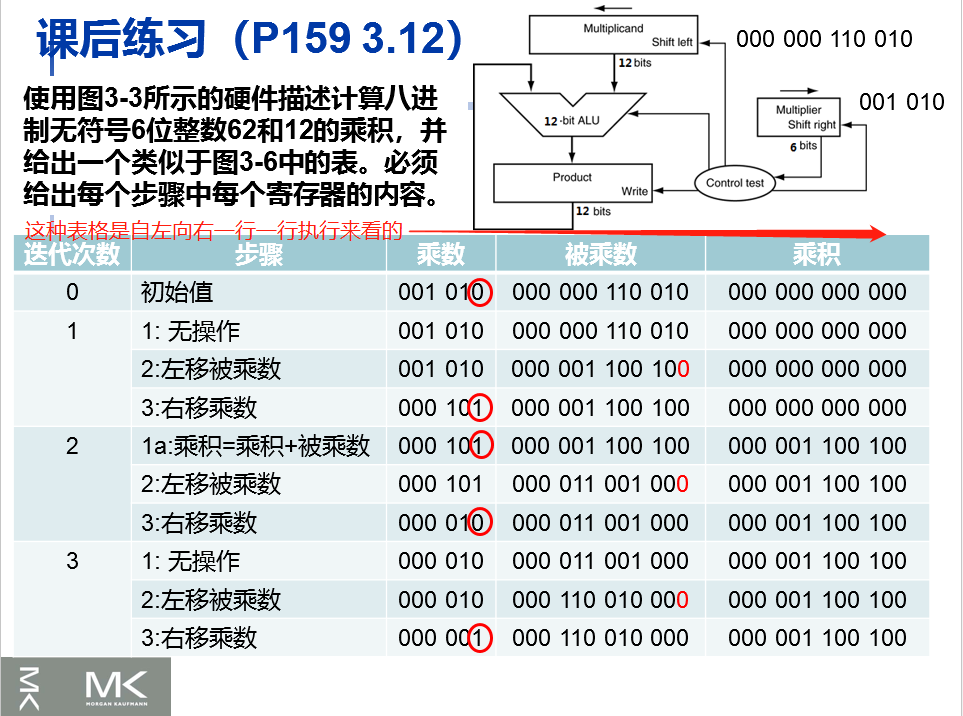
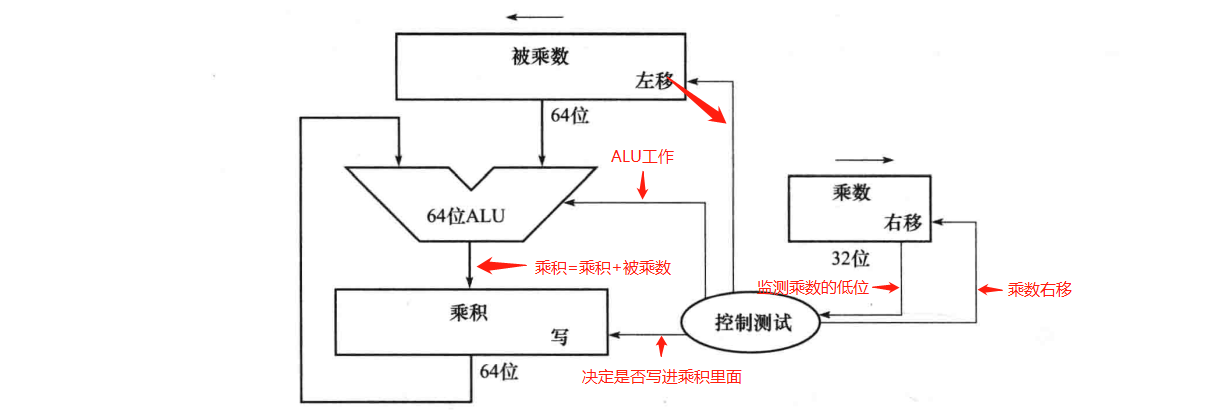
乘法器的优化

1. 这是根据硬件特性去优化的
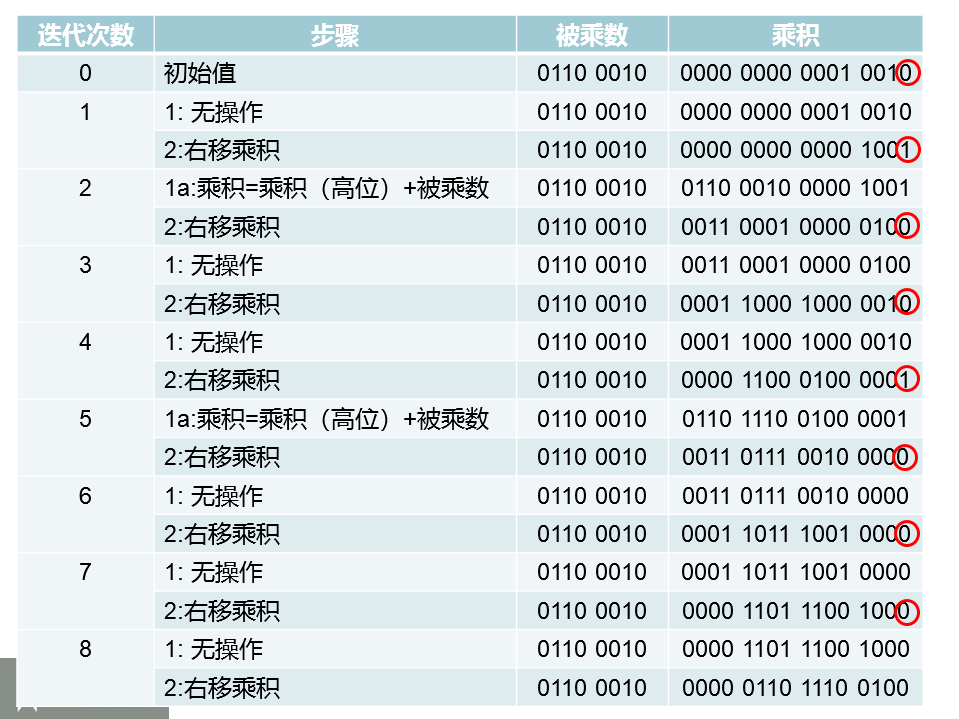
2. 我们先把乘数放到64位乘积寄存器的低32位，每次监测如果是1，把乘数高位32位和被乘数加起来，放到乘积寄存器的高32位上面去
3. 这样子一个迭代就过了一个循环周期只有两个时间周期

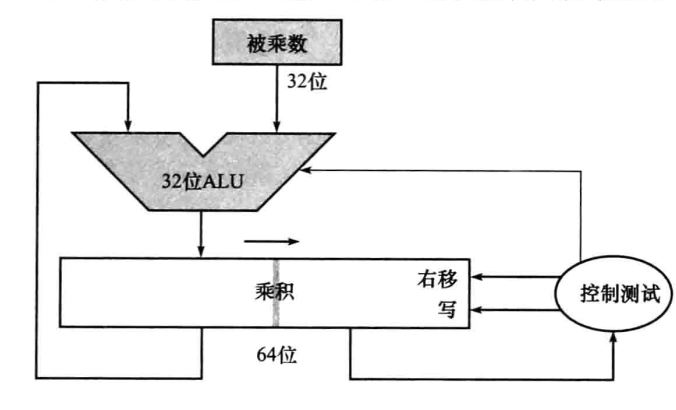
• 一对单独的32位寄存器来容纳64位的积，分贝是\(Hi\)和\(Lo\)。
• 为了产生正确的有符号积和无符号积，MIPS提供了两条指令：\(mult\) 和 \(multu\).
• 为了取得\(32\)位的整数积，通常使用\(mflo\)指令。

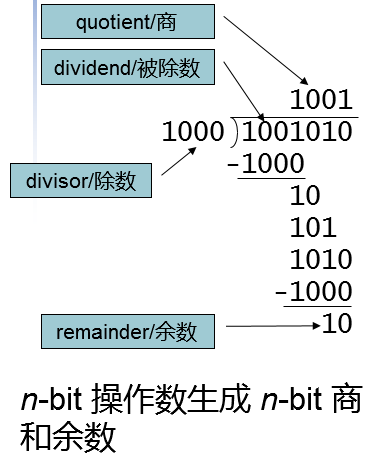
3.除法器

• 除数判0

• 除法步骤

1. 除数 ≤ 被除数

2. 商添加1，执行减法

3. 否则

4. 商添加0，从被除数中提取下一个bit

• 恢复余数法

1. 直接做减法，余数小于零再把除数加回去

• 带符号位的除法

1. 使用绝对值进行除法运算

2. 根据需要，调整商和余数的符号

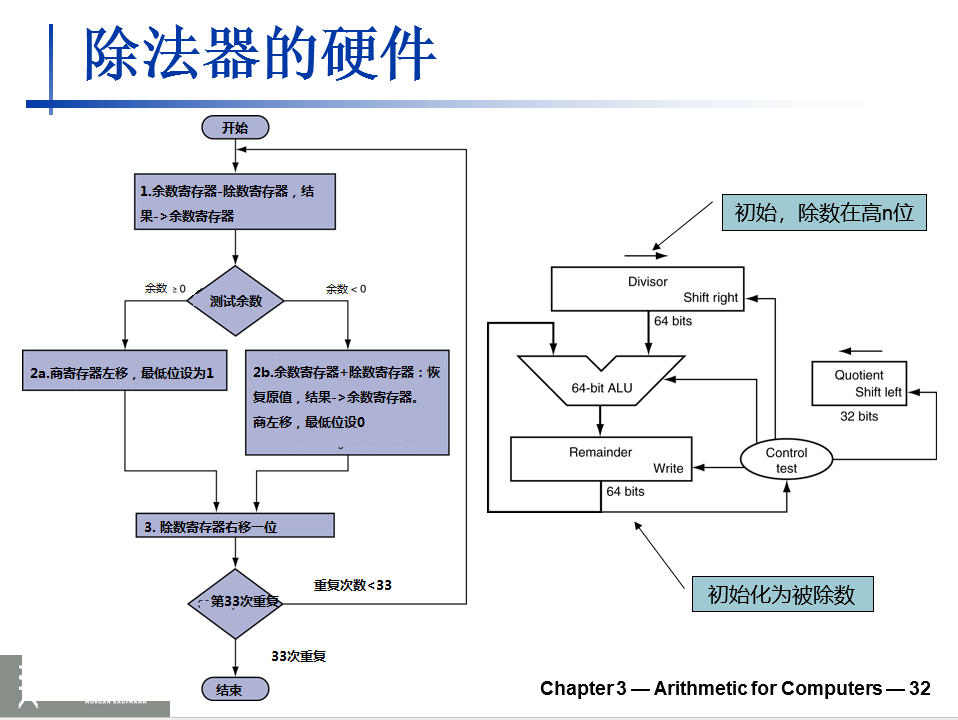
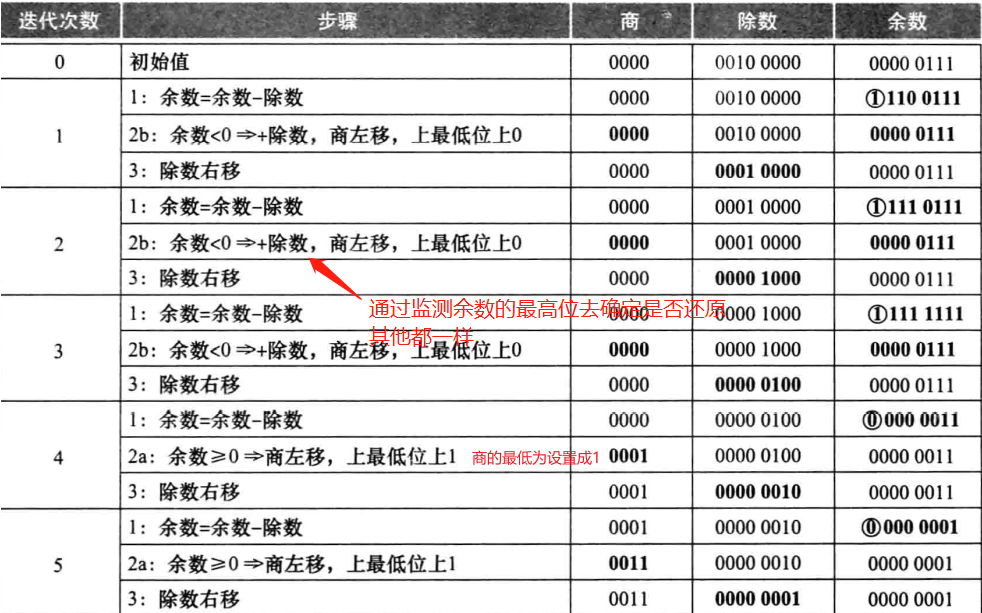
改进的除法器

改进前的74/21

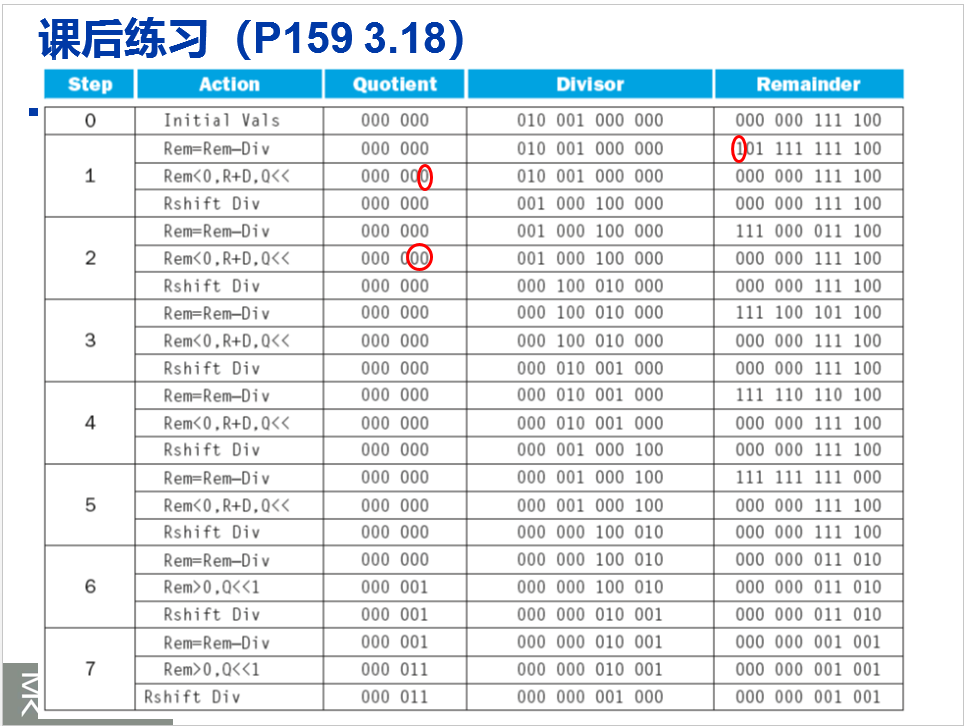
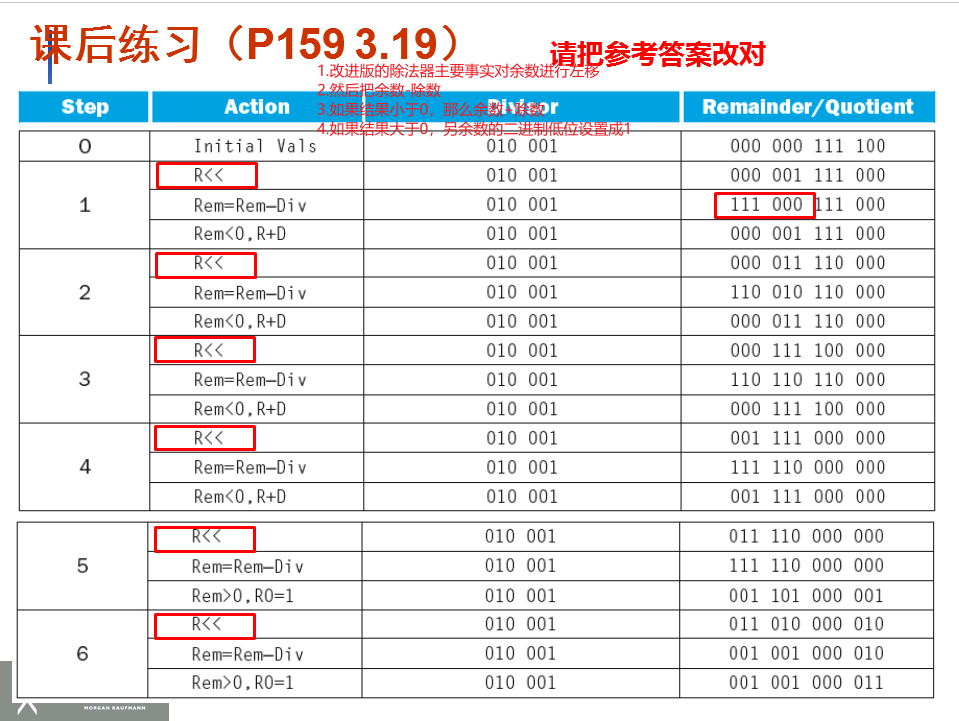
改进前是\(n+1\)次循环

改进后是\(n\)次循环

3.浮点数

浮点数加法