【XSY3350】svisor - 点分治+虚树dp
题目来源:NOI2019模拟测试赛(九)
题意:

吐槽:
第一眼看到题觉得这不是震波的完全弱化版吗……然后开开心心的码了个点分治
码到一半突然发现看错题了……心态崩了于是就弃疗手玩提答去了
于是就快乐垫底了
最后发现这是个最毒瘤的题……改题写+调了一天,代码长度再次进入前五排行榜
题解:
(明明是在线做法为什么不强制在线呢)
由于是询问树上某些关键点的信息,且$\sum k$比较小,所以考虑建出虚树处理询问;
如图,对于虚树上一个不是关键点的点$u$,显然他的最大监视半径就是$max\{r_v-dis_{u,v}|v是u的子节点\}$;

这个可以通过逆拓扑序在虚树上一遍DP求出来;
由于虚树的点数是$O(k)$的,所以可以直接用点分治预处理离每个点距离小于等于$r$的点数量,然后$O(logn)$处理虚树上所有点的询问;
但是这样做显然会有点被重复计算,如图,阴影部分的点就被计算了两次(图中是一条链,实际上可能还有其它分支也被重复计算了);
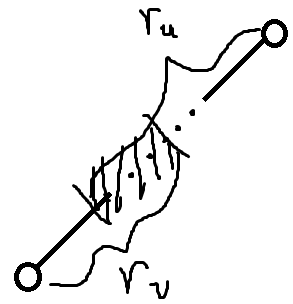
考虑被重复计算的部分有什么性质,容易发现它实际上就是距离$u$和$v$的监视半径重叠部分中心不超过$\frac{r_u+r_v-dis_{u,v}}{2}$的点集,显然这也可以当成类似的询问用点分治处理;
对虚树上每一对有重叠的父子都类似处理一遍,就可以减去所有重叠部分的额外影响,因此不用额外考虑被覆盖了三次四次甚至以上的点;
由于虚树的边数=点数-1,所以这一部分的时间复杂度显然是对的;
但是这样还有一个小问题:如图,如果重叠部分边长度为奇数,那么是找不到中心点的;

实际上这时中心点在一条边上,所以可以拆边,把树上每条原本的边都看成一个点,就可以解决了;
至此这道题终于做完了……具体实现的时候并不用把虚树真正建出来,只记录每个点的父节点和拓扑序即可;
总的时间复杂度$O((n+\sum k)logn)$,常数很大。
写的时候细节超多……外面的点分治要记一万个信息……轻松喜提200行+
代码:
1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<vector> 6 #include<cmath> 7 #include<queue> 8 #include<stack> 9 #define inf 2147483647 10 #define eps 1e-9 11 using namespace std; 12 typedef long long ll; 13 typedef double db; 14 struct edge{ 15 int v,next; 16 }a[200001]; 17 int n,m,u,v,K,S,rt,mxd,ans,tot=0,tim=0,fkfa[100001],dfn[100001],nmd[100001],head[100001],dps[100001],md1[100001],*s1[100001],md2[100001],*s2[100001],ddp[100001],dfdep[100001],dfrt[100001][20],dfds[100001][20],k[100001],r[100001],siz[100001],mx[100001],dep[100001],fa[100001][17]; 18 bool used[100001],isk[100001]; 19 stack<int>st; 20 vector<int>vec; 21 bool cmp(int a,int b){ 22 return dfn[a]<dfn[b]; 23 } 24 void add(int u,int v){ 25 a[++tot].v=v; 26 a[tot].next=head[u]; 27 head[u]=tot; 28 } 29 void dfs(int u,int ff,int dpt){ 30 dep[u]=dpt; 31 dfn[u]=++tim; 32 nmd[tim]=u; 33 fa[u][0]=ff; 34 for(int i=1;i<=16;i++)fa[u][i]=fa[fa[u][i-1]][i-1]; 35 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 36 int v=a[tmp].v; 37 if(v!=ff){ 38 dfs(v,u,dpt+1); 39 } 40 } 41 } 42 int lca(int u,int v){ 43 if(dep[u]<dep[v])swap(u,v); 44 int l=dep[u]-dep[v]; 45 for(int i=16;i>=0;i--){ 46 if((1<<i)&l){ 47 u=fa[u][i]; 48 } 49 } 50 if(u==v)return u; 51 for(int i=16;i>=0;i--){ 52 if(fa[u][i]!=fa[v][i]){ 53 u=fa[u][i],v=fa[v][i]; 54 } 55 } 56 return fa[u][0]; 57 } 58 int getfa(int u,int l){ 59 for(int i=16;i>=0;i--){ 60 if((1<<i)&l){ 61 u=fa[u][i]; 62 } 63 } 64 return u; 65 } 66 void dfsrt(int u,int fa){ 67 siz[u]=1; 68 mx[u]=0; 69 mxd=max(mxd,ddp[u]); 70 if(u<=n)dps[ddp[u]]++; 71 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 72 int v=a[tmp].v; 73 if(!used[v]&&v!=fa){ 74 dfsrt(v,u); 75 siz[u]+=siz[v]; 76 mx[u]=max(mx[u],siz[v]); 77 } 78 } 79 mx[u]=max(mx[u],S-siz[u]); 80 if(mx[u]<mx[rt])rt=u; 81 } 82 void dfsdep(int u,int fa,int ls,int dpt){ 83 siz[u]=1; 84 ddp[u]=dpt; 85 dfdep[u]++; 86 dfrt[u][dfdep[u]]=ls; 87 dfds[u][dfdep[u]]=dpt; 88 mxd=max(mxd,dpt); 89 if(u<=n)dps[dpt]++; 90 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 91 int v=a[tmp].v; 92 if(!used[v]&&v!=fa){ 93 dfsdep(v,u,ls,dpt+1); 94 siz[u]+=siz[v]; 95 } 96 } 97 } 98 void divide(int u){ 99 used[u]=true; 100 ddp[u]=mxd=0; 101 dfsdep(u,0,u,0); 102 md1[u]=mxd; 103 s1[u]=new int[mxd+1]; 104 for(int i=0;i<=mxd;i++){ 105 s1[u][i]=dps[i]; 106 if(i)s1[u][i]+=s1[u][i-1]; 107 dps[i]=0; 108 } 109 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 110 int v=a[tmp].v; 111 if(!used[v]){ 112 mxd=rt=0; 113 S=siz[v]; 114 dfsrt(v,u); 115 md2[rt]=mxd; 116 s2[rt]=new int[mxd+1]; 117 for(int i=0;i<=mxd;i++){ 118 s2[rt][i]=dps[i]; 119 if(i)s2[rt][i]+=s2[rt][i-1]; 120 dps[i]=0; 121 } 122 divide(rt); 123 } 124 } 125 } 126 void buildfaketree(){ 127 while(!st.empty())st.pop(); 128 vec.clear(); 129 sort(k+1,k+K+1,cmp); 130 st.push(k[1]); 131 for(int i=2;i<=K;i++){ 132 int z=lca(k[i],st.top()); 133 if(!isk[z])r[z]=-1; 134 while(!st.empty()&&dep[z]<dep[st.top()]){ 135 int x=st.top(); 136 st.pop(); 137 vec.push_back(x); 138 if(!st.empty()&&dep[z]<dep[st.top()])fkfa[x]=st.top(); 139 else fkfa[x]=z; 140 } 141 if(st.empty()||dep[z]>dep[st.top()])st.push(z); 142 if(k[i]!=z)st.push(k[i]); 143 } 144 while(!st.empty()){ 145 int x=st.top(); 146 st.pop(); 147 vec.push_back(x); 148 if(!st.empty())fkfa[x]=st.top(); 149 else fkfa[x]=0; 150 } 151 } 152 int getci(int u,int r){ 153 int nw,d1,d2,ret=0; 154 for(int i=dfdep[u];i;i--){ 155 nw=dfrt[u][i]; 156 d1=dfds[u][i]; 157 d2=dfds[u][i-1]; 158 if(d1<=r)ret+=s1[nw][min(r-d1,md1[nw])]; 159 if(i>1&&d2<=r)ret-=s2[nw][min(r-d2,md2[nw])]; 160 } 161 return ret; 162 } 163 void getans(){ 164 ans=0; 165 int u,ft,ds,mid,len=vec.size(); 166 for(int i=0;i<len;i++){ 167 u=vec[i]; 168 r[fkfa[u]]=max(r[fkfa[u]],r[u]-dep[u]+dep[fkfa[u]]); 169 } 170 for(int i=len-1;i>=0;i--){ 171 u=vec[i]; 172 r[u]=max(r[u],r[fkfa[u]]-dep[u]+dep[fkfa[u]]); 173 } 174 for(int i=0;i<len;i++){ 175 u=vec[i]; 176 ans+=getci(u,r[u]); 177 } 178 for(int i=0;i<len-1;i++){ 179 u=vec[i]; 180 ft=fkfa[u]; 181 ds=dep[u]-dep[ft]; 182 if(r[u]+r[ft]>=ds){ 183 mid=getfa(u,(r[u]-r[ft]+ds)/2); 184 ans-=getci(mid,r[u]-(r[u]-r[ft]+ds)/2); 185 } 186 } 187 } 188 void pt(int *s){ 189 for(int i=1;i<=n*2-1;i++)printf("%d ",s[i]); 190 puts(""); 191 } 192 int main(){ 193 memset(head,-1,sizeof(head)); 194 scanf("%d",&n); 195 for(int i=1;i<n;i++){ 196 scanf("%d%d",&u,&v); 197 add(u,n+i); 198 add(n+i,u); 199 add(v,n+i); 200 add(n+i,v); 201 } 202 dfs(1,0,0); 203 S=n*2-1; 204 mx[rt]=6666666; 205 dfsrt(1,-1); 206 memset(dps,0,sizeof(dps)); 207 divide(rt); 208 scanf("%d",&m); 209 while(m--){ 210 scanf("%d",&K); 211 r[0]=-1; 212 for(int i=1;i<=K;i++){ 213 scanf("%d",&k[i]); 214 scanf("%d",&r[k[i]]); 215 r[k[i]]*=2; 216 isk[k[i]]=true; 217 } 218 buildfaketree(); 219 for(int i=1;i<=K;i++)isk[k[i]]=false; 220 getans(); 221 printf("%d\n",ans); 222 } 223 return 0; 224 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号