密码学部分知识

密码学知识 简单概括

三个核心目标：机密性，完整性，可用性；

两类密码算法：对称密码和非对称/公钥密码；

Kerckhoffs原则（柯克霍夫原则）：即使密码系统的任何细节已为人悉知，只要密匙（key，又称密钥或秘钥）未泄漏，它也应是安全的。

机密性——对称加密

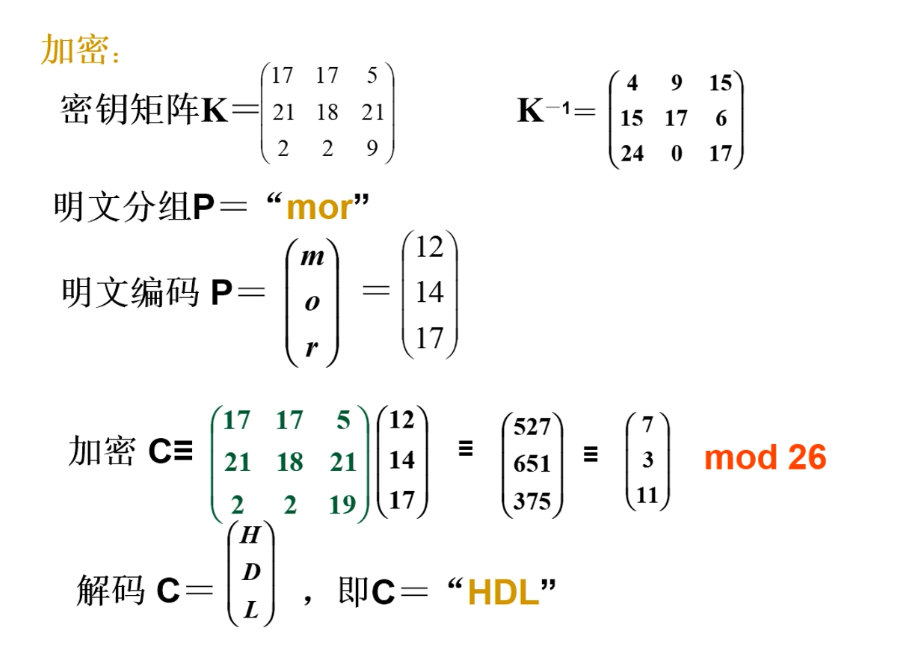
古典——Hill，基于矩阵乘法运算（矩阵的逆）

例子：

 

DES：分组长度/密钥长度；Feistel结构（分左右两半去做）；S盒；混淆vs扩散。

详叙：DES是一种用56位密钥（输入仍为64比特，8个校验位）来加密64位数据的方法。

S盒：将48bits压缩成32bits，8个S-Box，每个S-Box中都有一个置换表，每个盒输入6个比特，中间四位表示列，第一位和最后一位表示行，例如：输入（110101），对应表中第3行，第10列的数，假设表中为09，则输出为（1001）。非线性的。

 

设计特色：用S-盒实现小块的非线性变换，达到混乱目的；用置换P实现大块的非线性交换，达到扩散目的。

AES：分组长度/密钥长度

详叙：不属于Feistel，分组长度为128比特，密钥长度为128/192/256比特

流密码——RC4：随机的密钥流与明问异或

分组密码工作模式

ECB电码本，CBC密码链接模式（MAC消息认证），CTR计数器模式（并行），主要面对对称密码，组合工作模式：CCM。

详叙：面向多个分组。

ECB电码本：每个明文组独立地以同一密钥加密。简单的切割，独立加密[没有工作模式的工作模式]。长消息可能不安全，若分组明文相同，则得到的密文也相等，结构化明文。

CBC密码链接模式：加密算法的输入是当前明文组与前一密文组的异或。第一组明文与初始向量异或。缺点：错误传播，影响到当前解密分组和下一分组。利用缺点，可用于MAC消息认证。

计数器模式：加密计数器（counter）。

数学基础：大整数分解，欧拉定理，扩展欧几里德算法，离散对数，本原根。

详叙：

大整数分解：任意整数a>1都可唯一地因子分解为a=p1^a1 *p2^a2 *……pt^at，其中，pi均是素数，且p1<p2<……<pt，且每个ai>0。

欧拉定理：欧拉函数φ(n)：小于n且与n互素的正整数的个数。

a^φ(n)=1(mod n)，对于任意a,n，gcd(a,n)=1

扩展欧几里德算法:求乘法逆元。

离散对数：求x，以满足y=g^x (mod p)。

本原根：如果a是素数p的原根，则数a mod p, a^2 mod p, … , a^(p-1) mod p 是不同的并且包含1到p-1的整数的某种排列。

机密性——公钥加密

 

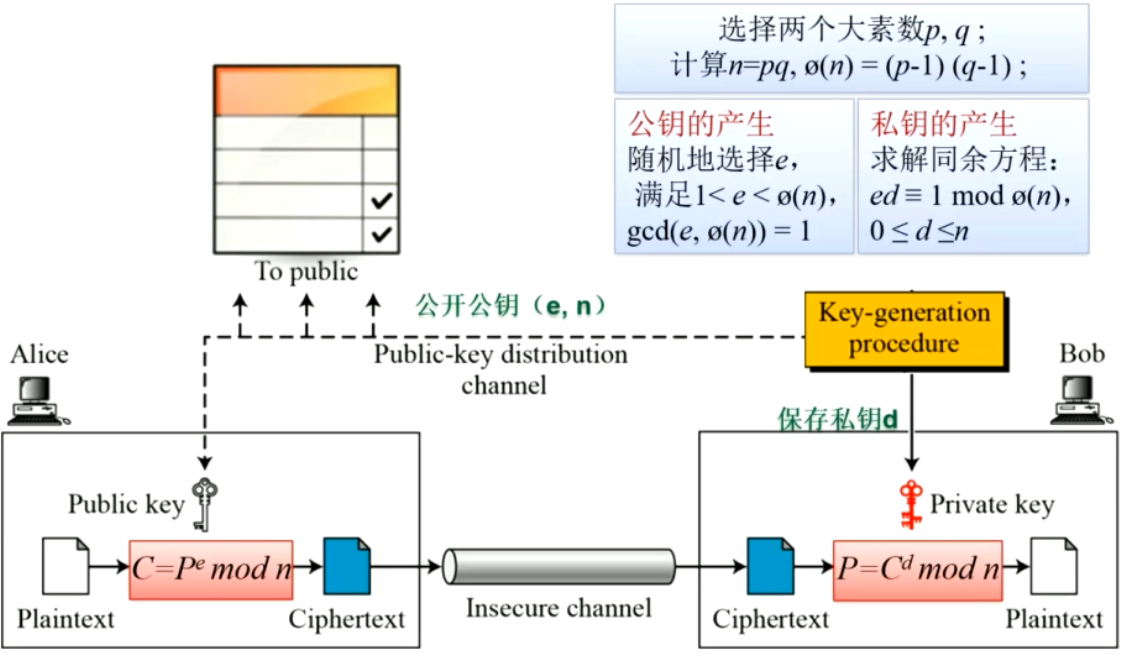
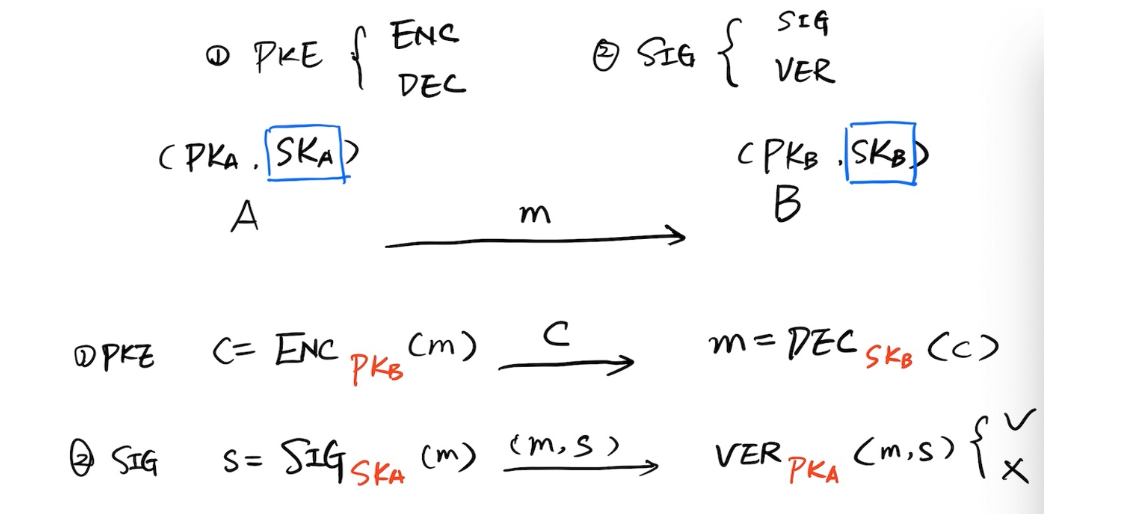
公钥密码：三种应用（公钥加密、数字签名、密钥交换）安全的基础基于陷门单向函数

RSA：密钥生成算法，加/解密，大整数分解

主要是：参数管理，密钥生成

 

实例：

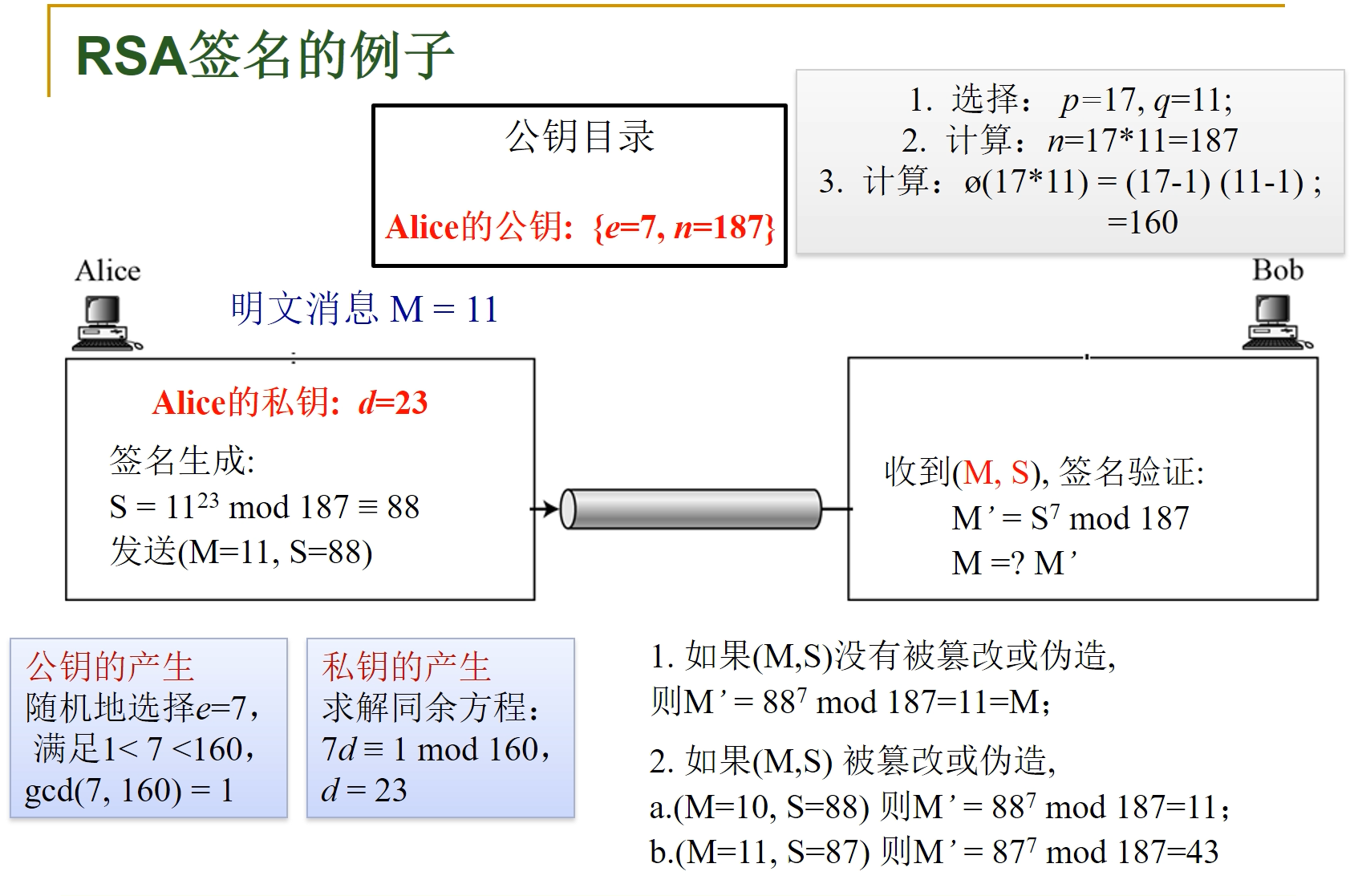
已知 p=17,q=11,e=7，加密M=88。

n=p*q=187,φ(n)=(p-1) *(q-1)=160,B的公钥是{e=7，n=187}.

B的私钥，因为ed=1 mod φ(n),所以7d=1 mod 160 ，得d=23.

A：加密C=88^7 mod 187=11；

B：解密M=11^23 mod 187 =88；

重点（无法抵御选择密文攻击）重点理解：

 

HASH：

Hash函数：单向性（找不到预先给定的Hash值找不到对应的数据块），弱抗碰撞（对于给定的y，找x，使H(x)=H(y)是计算困难的），强抗碰撞（生日攻击，找(x1,x2),x1不等于x2，H(x1)=H(x2)是计算困难的）；

典型算法：MD5 128bits， SHA-1 160bits SHA系列

典型应用：签名，消息认证码

详叙：哈希函数，单向函数。

完整性——消息认证码

对称密码体制，基于预共享密钥，不要求可逆 MAC=Ck(M)=C(K,M)

有k的才可以进行运算。

实现方式： HASH：HMAC框架

分组密码的CBC模式：DAA（DES-CBC）,CMAC

完整性——数字签名

不可伪造性

签名生成：s=SIG(m,sk)[输入：明文和私钥；输出：签名值]

签名验证：Ver(m,s,pk)[输入：明问，签名值，公钥；输出：验证结果（Y/N）]

RSA数字签名例子

 

RSA签名不满足强不可伪造性。

DSS： 320 bit 签名值

密钥交换

DH密钥交换，协议流程——会计算，离散对数问题，中间人攻击——缺少消息完整性保护，改进：SIG-DH(比较流行)、MAC-DH

详叙：

Diffie-Hellman密钥交换：交换会话密钥（不可传数据），密钥的值依赖于通信的参与者，安全性基于离散对数。随机数每次都要随机选

例子

 

掌握基础知识，为未来做好准备