在聊天机器人中加入专家决策机制对学生成绩、享受和焦虑的影响

(Effects of Incorporating an Expert Decision-making Mechanism into Chatbots on Students’ Achievement, Enjoyment, and Anxiety)

https://doi.org/10.30191/

一、摘要

研究目的：聊天机器人提供了一个解决传统教学中教学活动缺乏活力、教师查看个别学生学习情况困难以及无法及时反馈学生疑难等问题的机会。然而，传统的聊天机器人(C-chatbot)通常是作为信息提供者(即通过匹配对话中的关键字来提供相关信息)而不是作为决策顾问(即使用具有决策机制的知识库来帮助用户解决问题)。因此，本研究提出了一种基于专家决策的聊天机器人(EDM-chatbot)，以方便学生个体在学习过程中对知识的建构，通过聊天机器人学习减少学生的学习焦虑，保持学生的学习乐趣，获得更好的学习效果。

实验结果：结合专家决策知识的edm聊天机器人显著提高了学生的学习成绩和学习乐趣，减少了学生的学习焦虑。

二、研究问题

（1）使用EDM聊天机器人的学生是否比使用传统聊天机器人的学生学习成绩更好?

（2）使用EDM聊天机器人的学生是否比使用传统聊天机器人的学生学习焦虑更低？

（3）使用EDM聊天机器人的学生是否比使用传统聊天机器人的学生学习乐趣更高？

三、研究设计

（一）基于专家决策的聊天机器人的开发

本研究使用IBM Watson为一门科学课程的地理气候单元构建了一个聊天机器人。气候变化是一个复杂的环境问题，可以用来考察学生通过课堂交流获得的对气候变化及其相互作用的理解。Jakobsson等人(2009)在一项通过笔试进行的研究中发现，学生对气候变化的理解较差，笔试并不能明确地揭示学生学到的知识。因此，本研究认为如果使用交际法，学生对气候变化等复杂问题的理解或意义构建会更好。

1.基于ID3算法构建决策树

表1显示了用于构建ID3决策树的专家知识示例(Quinlan, 1983)。天气有16个分类(即C1、C2…C16)，由海拔、冬冷夏凉、纬度、降雨、旱季、夏干、静止锋、针叶林、雪(无雨)9个构式组成，它们各自有不同的临界特征值。

表1训练数据集S

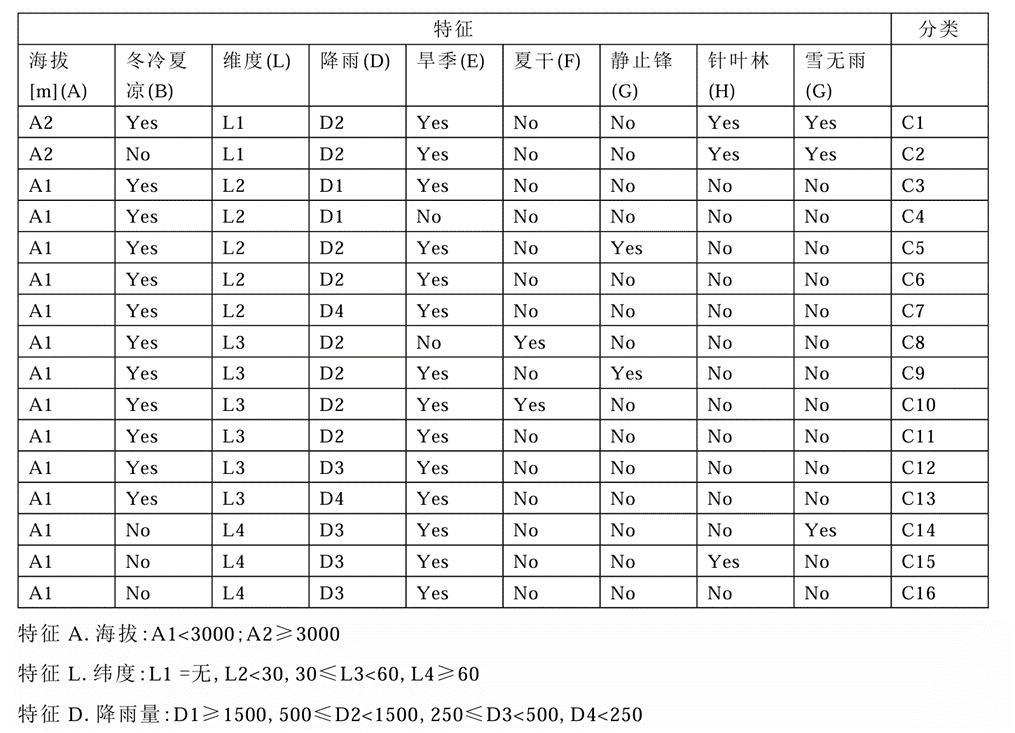
为了开发正确分类训练样例的决策规则，ID3首先选择一个特征，然后使用选择的特征将样例分类为子类来执行特征测试，从而形成有效的决策树。

①  计算信息熵：度量样本纯度的指标，熵值越小，样本集纯度越高。

 

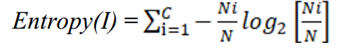
②  计算基于每个特征的信息增益（表示在使用指定属性的特定条件下信息复杂性降低的程度），挑选最优特征，即信息增益最大的特征作为根节点。

 

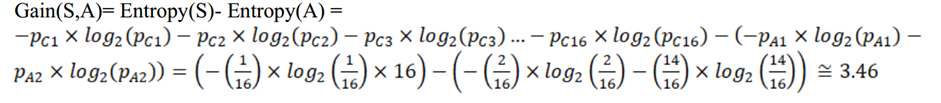
③  分割数据：根据选定的最优特征分割数据，为每个分割创建子节点。

④  递归构建：对每个子节点重复上述过程，直到满足停止条件（例如所有样本都属于同一类别，或者达到了树的最大深度）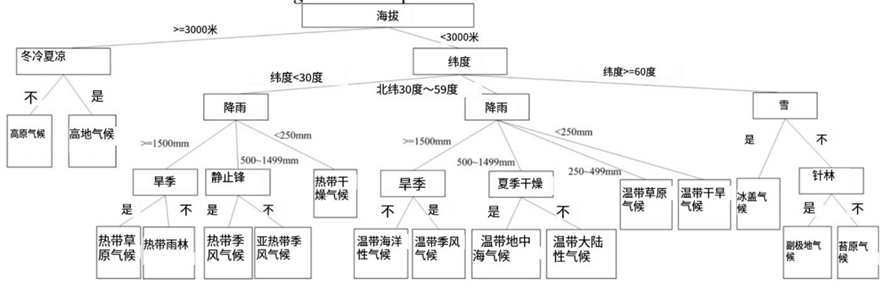

图1气候决策树

2.用python生成决策树简单实例

表2训练样本集D

 

python源代码如下：

#! Decision Tree(ID3算法信息增益Gain)

# ? 构建数据集
#  返回一个元组 (dataSet,labels)
def createDataSet():  # 创造示例数据
    dataSet = [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
               ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
               ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
               ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
               ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
               ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
               ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],

               ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
               ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
               ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
               ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
               ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
               ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
               ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']]
    labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']  # 六个特征
    return dataSet, labels


# ? 计算信息熵
#  返回输入样本集dataSet的信息熵 Ent
from math import log
def calEnt(dataSet):
    sampleCounts = len(dataSet)  # 样本集的样本数
    labelCounts = {}  # key为标签值label（好瓜、坏瓜），value为对应标签key在样本集中出现的次数
    for sample in dataSet:  # 遍历样本集dataSet中每个样本sample
        label = sample[-1]  # 标签label为样本sample的最后一个元素值
        if label not in labelCounts.keys():  # 如果该标签label不在字典labelCounts的key值中
            labelCounts[label] = 0  # 则新增该key，并赋初值0
        labelCounts[label] += 1  # 对遍历到的每个sample统计其所属标签的个数
    Ent = 0.0  # 信息熵初始化
    for key in labelCounts:
        pro = float(labelCounts[key]) / sampleCounts  # 具体标签占总样本数的比例pro
        Ent -= pro * log(pro, 2)  # 计算样本集dataSet的信息熵Ent
    return Ent


# ? 按给定特征值划分出样本子集
#  指定特征列的索引index，对特征值==value的样本划分出来为一个样本子集retDataSet，并对这些样本的value去掉，返回样本子集 retDataSet
def splitDataSet(dataSet, index, value):  # index是指定特征列的索引，value是该特征下的某一特征值
    retDataSet = []
    for sample in dataSet:  # 遍历样本集dataSet中的具体样本sample
        if sample[index] == value:  # 找到目标特征值value的索引
            # 去除特征值==value这些样本的vlaue值
            reducedSample = sample[:index]  # 剪下目标索引前的列表
            reducedSample.extend(sample[index + 1:])  # 将目标索引后的列表添加到索引前列表的后面
            retDataSet.append(reducedSample)  # 将sample[index]==value并去除该vlaue的样本添加到retDataSet样本集中
    return retDataSet


# ? 选取当前样集下的最优划分特征索引
#  返回最优划分特征的索引 bestFeatureIndex
def chooseBestFeatureToSplit(dataSet):
    featureCounts = len(dataSet[0]) - 1  # 获取当前样本集的特征个数，-1是因为最后一列是标签
    baseEnt = calEnt(dataSet)  # 计算当前样本集的信息熵Ent(D)
    bestGain = 0.0;
    bestFeatureIndex = -1  # 初始化最优信息增益bestGain、最优特征bestFeature
    for i in range(featureCounts):  # 遍历每个特征，求各自的信息增益Gain
        featValList = [sample[i] for sample in dataSet]  # 第i个特征下所有样本出现的特征值（有重复）
        uniqueVals = set(featValList)  # 第i个特征的可能特征值（无重复）
        newEnt = 0.0  # 初始化信息熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)  # 根据特定的特征值value划分出的样本子集
            pro = len(subDataSet) / float(len(dataSet))  # 划分出的样本子集占总样本数的比例
            newEnt += pro * calEnt(subDataSet)  # 计算各特征值的熵并加和
        Gain = baseEnt - newEnt  # 计算信息增益Gain(D,a)
        if (Gain > bestGain):  # 求最大的信息增益Gain
            bestGain = Gain
            bestFeatureIndex = i  # 获取最优划分特征的索引
    return bestFeatureIndex


# ? 求样本集中出现次数最多的标签
#  用于叶子节点的取值，返回样本集中出现次数最多的标签 sortedLabelCounts[0][0]
import operator


def majorLabel(labelList):
    labelCounts = {}  # key为标签（好瓜/坏瓜），value为标签在labelList中出现的次数
    for label in labelList:  # 遍历所有样本的标签
        if label not in labelCounts.keys():  # 如果该标签不在labelCounts的key值中
            labelCounts[label] = 0  # 则增加该key值，并赋初值=0
        labelCounts[label] += 1  # 对labelCounts中已有的标签计数+1
    sortedLabelCounts = sorted(labelCounts.items(), key=operator.itemgetter(1), reverse=True)  # 根据value值逆序排序labelCounts
    return sortedLabelCounts[0][0]  # 返回第一个元素的第一个元素（标签）


# ? 生成决策树主方法
#  递归生成决策树 decisionTree
#  递归是逐级由深向浅的返回
def createTree(dataSet, labels):
    labelList = [sample[-1] for sample in dataSet]  # 返回当前样本集dataSet中所有样本的标签（有重复值列表）
    # 跳出递归，生成叶子节点（好瓜/坏瓜）
    if labelList.count(labelList[0]) == len(labelList):  # 如果labelList中的标签完全相同
        return labelList[0]  # 则直接返回该标签
    if len(dataSet[0]) == 1:  # 如果当前样本集dataSet的样本长度==1（只剩最后一列标签，无特征可供继续划分又不满足所有标签相同）
        return majorLabel(labelList)  # 就返回出现次数最多的标签作为叶子节点

    bestFeatureIndex = chooseBestFeatureToSplit(dataSet)  # 获取当前样本集dataSet最优划分特征的索引
    bestFeature = labels[bestFeatureIndex]  # 获取当前样本集dataSet的最优划分特征
    decisionTree = {bestFeature: {}}  # 字典存储决策树的信息
    del (labels[bestFeatureIndex])  # 删除已经选出的特征
    featureVals = [sample[bestFeatureIndex] for sample in dataSet]  # 样本集中所有样本中的最优特征对应的特征值组成的列表（有重复值）
    uniqueVals = set(featureVals)  # 最优特征对应的所有可能取值（无重复值）
    for value in uniqueVals:  # 遍历最优特征所有可能的取值value
        subLabels = labels[:]  # 将最优特征去除后的特征列表传递给subLabels
        decisionTree[bestFeature][value] = createTree(splitDataSet(dataSet, bestFeatureIndex, value),
                                                      subLabels)  # 递归生成decisionTree
    return decisionTree


# ? 对验证样本进行分类
#  返回一个对样本分类后的标签classLabel
def classify(decisionTree, features, testSample):
    rootFeature = list(decisionTree.keys())[0]  # rootFeature：根节点是何种特征
    rootDict = decisionTree[rootFeature]  # rootDict为根节点的value值，是一个字典
    rootFeatureIndex = features.index(rootFeature)  # 获取根节点在特征列表中的索引
    for value in rootDict.keys():  # value为特征rootFeature的不同取值，并遍历value
        if testSample[rootFeatureIndex] == value:  # 如果待测样本的该特征的特征值==value
            if type(rootDict[value]) == dict:  # 如果该特征值value对应的value'是一个字典
                classLabel = classify(rootDict[value], features, testSample)  # 则需要递归继续向决策树的下面结点查询
            else:  # 如果该特征值value对应的value'是一个单独的值（标签）
                classLabel = rootDict[value]  # 则该值就是要找的标签
    return classLabel  # 返回该样本testSample的标签


if __name__ == '__main__':  # 如果在当前模块/文件下执行，将会指定下述代码
    dataSet, labels = createDataSet()
    decisionTree = createTree(dataSet, labels)
    print(f"\ndecisionTree={decisionTree}\n")  # 输出决策树模型结果
    # 验证集
    features = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']  # 特征列表
    testSample = ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']  # 待测样本
    print(f"测试结果1sampleLabel= {classify(decisionTree, features, testSample)}\n")  # 输出测试结果

    features = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']  # 特征列表
    testSample = ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑']  # 待测样本
    print(f"测试结果2sampleLabel= {classify(decisionTree, features, testSample)}\n")  # 输出测试结果

    features = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']  # 特征列表
    testSample = ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑']  # 待测样本
    print(f"测试结果3sampleLabel= {classify(decisionTree, features, testSample)}\n")  # 输出测试结果

 

图2运行结果

 

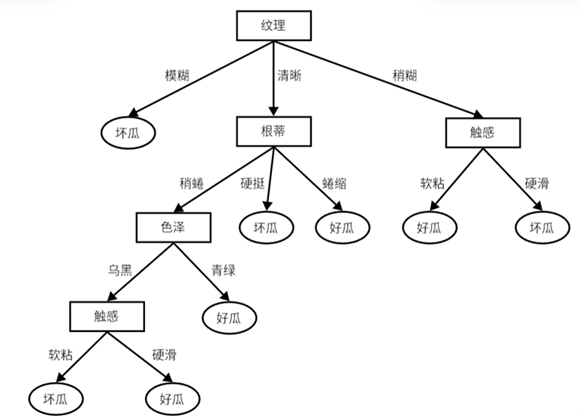
图3可视化树状结构图

3.EDM聊天机器人系统与C聊天机器人系统

聊天机器人都具有学习功能，并采用IBM Watson中的模糊匹配技术，使其与学生的对话更加顺畅。模糊匹配使系统能够处理词干提取、拼写错误或部分匹配。

 

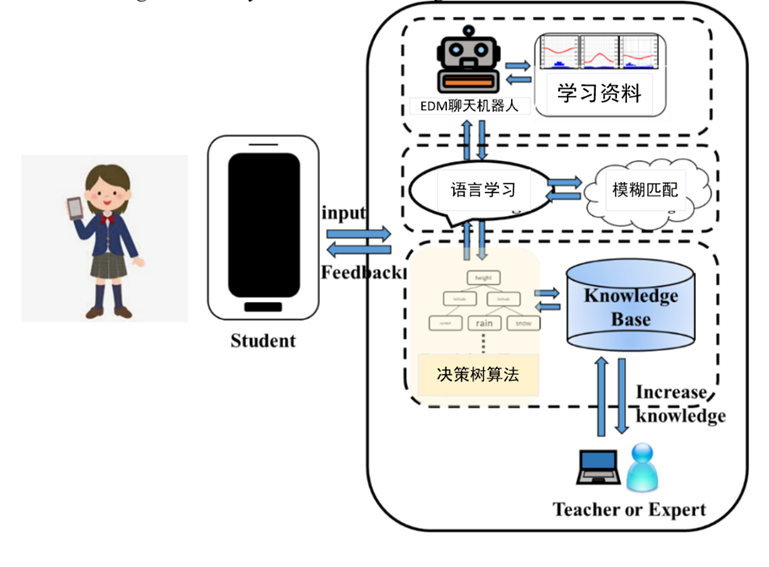
图4 EDM聊天机器人的系统架构图

 

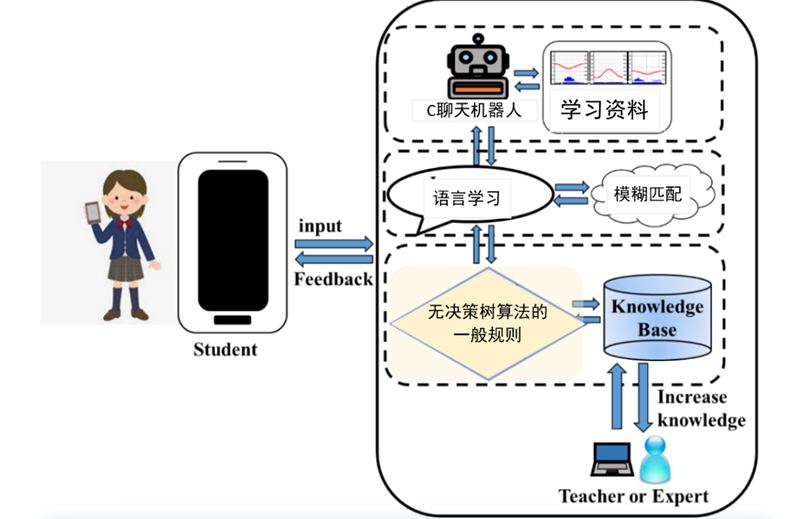图5 C聊天机器人的系统架构图

图6展示了传统聊天机器人的对话设计，系统会先向学生提出一个问题，紧接着为学生提供多个选择信息，然后根据学生选择提供数据库中相应的学习内容。传统聊天机器人很容易陷入相同的对话循环，所以当学生想要与其交互时，可以通过单击对话项进行选择。如果学生不只是想点击选项，也可以直接回复想说的内容。EDM聊天机器人的对话经过算法处理，基于专家知识和决策树的对话更加精简，学生更容易组织自己的知识，找到自己的学习目标，如图7所示。

 

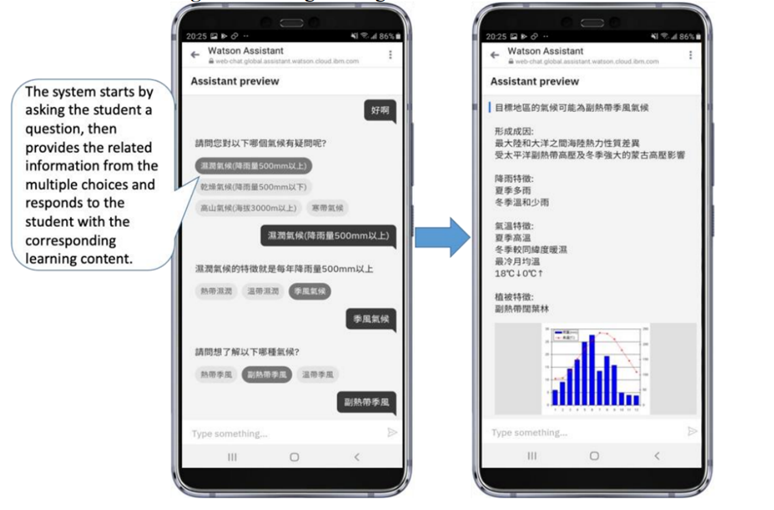
图6 C聊天机器人的对话设计

 

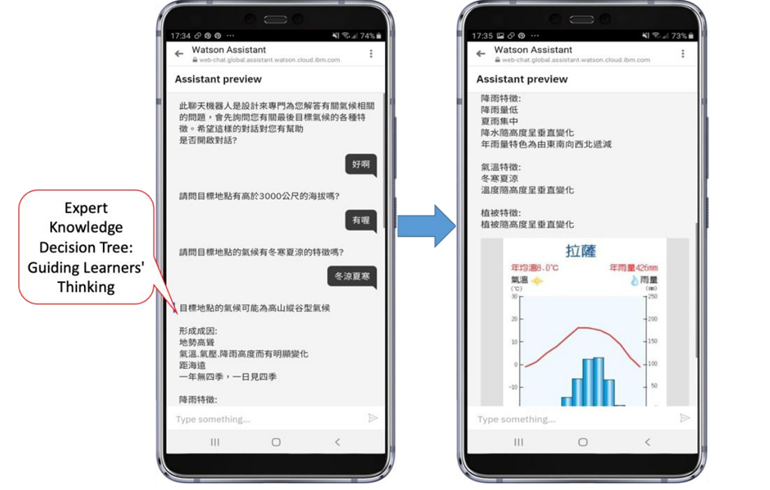
图7 EDM聊天机器人的对话设计

（二）实验对象

选取两个班的高中生，平均年龄17岁。一组(N = 35)为实验组，使用EDM聊天机器人；另一组(N = 35)为对照组，使用c聊天机器人。由同一个老师对两组学生进行教授。

（三）实验过程

 

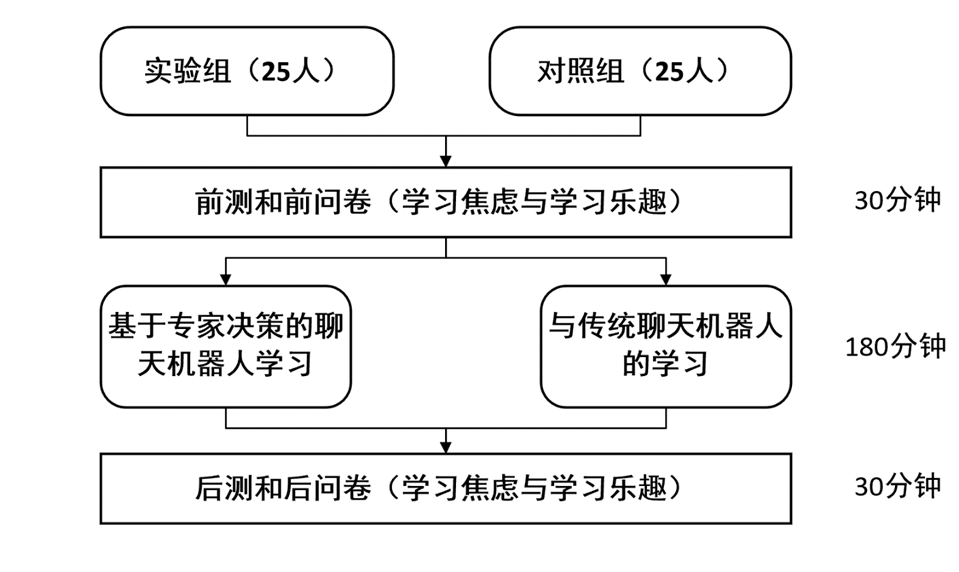
四、研究结果

根据研究数据，首先采用Kolmogorov-Smirnov检验进行正态性检验;发现各组数据均不符合正态分布(即ShapiroWilk的p值均小于0.05)。因此，采用非参数分析的统计方法。

（一）学习成绩

首先采用Wilcoxon signed-rank检验比较各组学习成绩前测和后测的差异，如表3所示。结果显示，对照组学生后测学习成绩(M = 57.429, SD = 11.464)显著高于前测学习成绩(M = 53.143, SD = 12.071) (Z = -2.044*， p < 0.05)。同时，实验组后测学习成绩(M = 65.714, SD = 15.202)显著高于前测学习成绩(M = 57.143, SD = 23.082) (Z = -2.736**， p < 0.01)。因此，这两种系统都有助于自我学习。

表3两组学习成绩的威尔克科森检验结果

 

其次，采用Mann-Whitney U检验比较两组前测结果无显著差异。最后，再次进行Mann-Whitney U检验，比较两组的后测结果。结果发现，实验组的学习成绩(M = 65.714, SD = 15.202)显著优于对照组的学习成绩(M = 57.429, SD = 11.464) (U = 416.500, p < 0.05)，见表4。

表4两组学习成绩后测的曼-惠特尼U检验结果

 

（二）学习焦虑

首先，采用Wilcoxon sign -rank检验比较两组学习焦虑前测和后测结果，见表5。结果显示，对照组焦虑前测(M = 3.083, SD = 0.439)与后测(M = 3.117, SD = 0.279)差异无统计学意义(Z = -0.432, p > 0.05)。实验组焦虑前测(M = 2.844, SD = 0.490)与后测(M = 2.390, SD = 0.611)差异有统计学意义(Z = -2.893**， p < 0.01)。因此，EDM聊天机器人有助于显著降低学生的学习焦虑。

表5两组学习焦虑的威尔克科森检验结果

 

其次，采用Mann-Whitney U检验比较两组学习焦虑前测结果无显著差异。最后，再次进行Mann-Whitney U检验，比较两组的学习焦虑后测结果。结果发现，实验组的学习焦虑(M = 2.390, SD = 0.611)显著低于对照组的学习焦虑(M =3.117, SD = 0.279) (U =216.500***， p < .001)，见表6。

表6两组学习焦虑后测的曼-惠特尼U检验结果

 

（三）学习乐趣

首先，采用Wilcoxon符号秩检验比较各组学习乐趣前测和后测的差异，见表7。结果显示，对照组的享受后测(M = 2.790, SD = 0.801)显著低于前测(M = 3.419, SD = 0.711)(Z = -3.105**， p < 0.01)。这一发现表明，当学生使用c聊天机器人进行自我学习时，他们感受到的学习乐趣较低。实验组享受前测(M = 3.324, SD = 0.810)与享受后测(M = 3.343, SD = 0.865)差异无统计学意义(Z = 0.082, p > 0.05)。

表7两组学习乐趣的威尔克科森检验结果

 

其次，采用Mann-Whitney U检验比较两组学习享受前测结果无显著差异(U = 57万;Z = -0.524;(p > . 05)。最后，再次进行Mann-Whitney U检验，比较两组的学习后享受程度。结果发现，实验组的学习享受(M = 3.343, SD = 0.865)显著高于对照组的学习享受(M = 2.790, SD = 0.801) U = 404.000*， p < 0.05)，见表8。

表8两组学习乐趣后测的曼-惠特尼U检验结果

 

五、结论

本研究利用IBM Watson构建了一个EDM聊天机器人，并将专家决策融入到多轮对话机制中，为学生提供自适应学习。在人工智能算法系统中，避免了与文化、宗教和性别相关的有偏见的词语，为学习者提供了一个公平的竞争环境，新的算法可以通过智能分析、诊断、预测、治疗和预防实现更接近人类的表现，为学生提供自适应学习(Yang, 2021)。实验结果表明，EDM聊天机器人在提高学生学习成绩、减少学习焦虑、增加学习乐趣方面比传统聊天机器人更有效。

尽管有积极的发现，但本研究仍有一些值得注意的局限性。

首先，如果学生的答案与手头的问题无关，聊天机器人可能不得不从头开始对话，这可能会让学生感到不耐烦。建议未来的研究首先收集学生在传统课堂上的学习成果和参与度，以便将学生使用e-learning结合AI机制进行自主学习的表现与教师在无法考虑任何个性化反应的传统课堂上教授的学生的表现进行比较。

其次，本研究仅在地理气候单元中使用聊天机器人，自我学习时间有限且教师并未对学生的学习进行干预。因此建议未来的研究在更长的时间内尝试针对不同学科和课程的聊天机器人的高交互性设计，教师在进一步的研究中可以成为一个独立变量。