EM算法浅析(一)-问题引出

EM算法浅析，我准备写一个系列的文章：

• EM算法浅析(一)-问题引出
• EM算法浅析(二)-算法初探

一、基本认识

EM（Expectation Maximization Algorithm）算法即期望最大化算法。这个名字起的很理科，就是把算法中两个步骤的名称放到名字里，一个E步计算期望，一个M步计算最大化，然后放到名字里就OK。
EM算法是一种迭代算法，是1977年由Demspster等人总结提出，用于有隐含变量的概率模型参数的极大似然估计，或极大后验概率估计。这里可以注意下，EM算法是针对于有隐含变量的问题，而且类似极大似然估计，也就是原有的极大似然估计的方法解决不了具有隐含变量的问题，所以才产生了EM算法。也就是说如果 概率模型的变量都是观测变量，那么给定数据可以直接用极大似然腹肌法或者贝叶斯估计法来估计模型参数。（EM算法是初值敏感的，而且EM算法不能保证找到全局最优解。）
起初了解此算法的时候，很多问题萦绕心头，却总是看不太懂，很多介绍也都有自己的理解和侧重点，那么我就得写一个自己的版本，首先我遇到的问题大致如下(不断补充中)，如果你遇到的问题跟我相仿，不妨看下这篇博客：

1. 为什么要迭代，有什么困难？
2. E步到底是干嘛的？
3. M步又在干啥啊？

二、问题引出

在各种理论知识的介绍中，例子总是那么的平易近人，我们就从李航老师书中的例子（三硬币模型）的解释丰富版出发：
假设有3枚硬币，分别记作A，B，C.这些硬币正面出现的概率分别为\(\pi, p, q\).接下来我们进行一个实验：先掷硬币A，并根据其结果选出硬币B或者C，正面选择硬币B，反面选择硬币C；然后掷选出来的硬币（B或者C），记录掷出来的结果，正面记作1，掷出反面记作0；独立重复10次实验（这里也可以泛化为重复n次实验），得到的结果如下：

\[1，1，0，1，0，0，1，0，1，1 \]

于是我们有个问题需要解决，现在只给你结果序列，例如上面的\(1，1，0，1，0，0，1，0，1，1\)，再告诉你上述规则，而不能观测掷硬币过程的结果，让你去估计三枚硬币正面出现的概率。也就是告诉你，我是这样抛硬币的，结果给你看，让你求\(\pi, p, q\)的具体值是多少。例如你可以根据自己的经验瞎猜说三枚硬币都是均匀的，即\(\pi=0.5, p=0.5, q=0.5\)。这当然没问题，但是你没有用上述给你的结果数据（01序列），也许用上这个数据，然后根据概率知识，我们能猜的更准。那么我们就需要用到EM算法，来个更加精准的版本了。（这里留一个问题，为什么我们不用MLE（最大似然估计）呢？）
我们先介绍下所用到的变量的物理意义：用\(y\)表示观测变量，也就是上述观测结果中的0或者1；用\(\theta = (\pi, p, q)\)表示所要求的参数；随机变量z表示隐变量，表示没有观测到的掷硬币A的结果。也就是我们知道y到底是等于0还是1，而不知道此时z是0还是1（正面还是反面）。所以此时某一次y出现0或者1的概率可以表示为：

\[P(y|\theta)=\sum_z{P(y,z|\theta)}=\color{blue}{\sum_z}{P(z|\theta)P(y|z,\theta)}=\pi p^y(1-p)^{1-y}\color{red}+(1-\pi)q^y(1-q)^{1-y} \tag{1} \]

再来解释下这个式子具体表示了什么，简单一句话来说应该就是用全概率公式，计算了在\(\theta={\pi,p,q}\)这些参数的情况（条件）下，在随机变量z的各种情况下（累和），y出现的概率\(P(y\|\theta)\)。我们来举个栗子说一下，例如，我们看序列的第一个值为1(即y=1)，那么y=1出现是有两种情况的（即两种情况下的概率之和），情况如下：①当掷硬币A为正面，选择硬币B，掷硬币B出现正面；②当掷硬币A为反面，选择硬币C，掷硬币C出现正面。上述两种情况，也就是我们看不到的中间掷硬币的结果，也就是上面说的隐含变量（z）。那这两种情况相加就对应上述公式中对随机变量z蓝色的求和符号和后面红色的加号的解释。所以，当y=1时，我们重新写一遍上述公式，如下：

\[P(y=1|\theta)=\sum_z{P(y=1,z|\theta)}=\color{blue}{\sum_z}{P(z|\theta)P(y=1|z,\theta)}=\pi p\color{red}+(1-\pi)q \tag{2} \]

到现在，其实我们只是理解了一个与最后观测结果有关系的一个概率公式，而且还是特例。接下来我们要加速了...
我们将观测数据表示为\(Y=(Y_1,Y_2,...,Y_n)^T\)，表示每次最终掷硬币的结果；未观测的数据表示为\(Z=(Z_1,Z_2,...,Z_n)^T\)，表示每次中间掷硬币做选择（下一步掷B还是C）的结果。所以，观测数据的似然函数我们可以表示为：

\[P(Y|\theta)=\sum_Z{P(Y,Z|\theta)}=\sum_Z{P(Z|\theta)P(Y|Z,\theta)} \tag{3} \]

如果这个式子看不懂，暂时没有关系，我们继续讲。这个式子其实就是Y的联合概率，即\(P(Y)=P(Y=Y_1)\*P(Y=Y_2)\*...\*P(Y=Y_n)\)，这里故意把乘号（*）写出来了（转变为下面式子的累积符号）。也就是最终出现那个01串中，每次结果的概率之积。式子最开始为什么没有Z呢？因为对于每一种\(P(Y=Y_i)\)都求对Z的全概率和，所以上式可以变为：

\[P(Y|\theta)=\prod_{j=1}^{n}[\pi p^{y_i}(1-p)^{1-y_i}+（1-\pi）q^{y_i}(1-q)^{1-y_i}] \tag{4} \]

上式（4）和公式（3）是一样的，那么Z呢？Z在公式（4）中的中括号中拆开了。因为Z有两种情况，现在把这两种情况都考虑了，然后求和，就是总的发生的概率。到这里，公式（3）和公式（4）应该清楚了。所以，也就相当于，我们现在算了一个出现当前观测结果的概率\(P(Y\|\theta)\)，那么当前结果既然出现了，就证明存在即合理的，要安排一组参数\(\theta\)使得现在的观测结果出现的概率最大，即最大似然估计（MLE）：

\[\hat{\theta}=arg{max}_{\theta}logP(Y|\theta) \tag{5} \]

哈，终于有目标，接下来就是怎么求，然而不幸的是这个问题是没有解析解（解析解就是通过公式求出来未知变量的值，例如你解方程解出来x的值是多少，得出来的值就是x的解析解。），只能通过迭代的方法求解。这时EM算法应运而生的时候了。就是这类问题，无法获得解析解，要通过EM算法来求解。那EM算法怎么求得这个模型的参数呢？我们接着来看！！！

一般来说，用Y表示观测随机变量的数据，Z表示隐随机变量的数据。Y和Z合在一起称为完全数据，观测数据Y又称为不完全数据。假设给了观测数据Y，其概率分布式\(P(Y\|\theta)\)，其中\(\theta\)是需要估计的模型参数，那么不完全数据的似然函数是\(P(Y\|\theta)\)，对数似然函数是\(L(\theta)=logP(Y\|\theta)\)；假设Y和Z的联合概率是\(P(Y,Z\|\theta)\)，那么完全数据的对数似然函数是\(logP(Y,Z\|\theta)\)。
之前，其实一直没清晰的了解这里为什么不直接按照公式（5）求最大值，难道只是因为\(logP(Y|\theta)\)并不是独立存在的，其中有隐含变量Z？例如在隐马尔可夫的模型训练问题中（可以看博文），海藻的例子中，我们观测的是海藻序列\(O={dry,damp,soggy}\)，但是明显是天气的因素决定性的影响了这种显式的状态，因此对海藻进行建模时候，就把隐含的天气因素考虑进去；又或者在上述三硬币模型中，每组显式的数据，我们并不清楚是投掷的硬币B还是硬币C；从而遇到信息缺失的情况，就会导致我们无法单纯的用极大似然估计来求得解析解。这应该就是EM创新的点吧。

三、EM算法初探

说了这么多，给了一个典型的问题，引出来EM算法，那EM算法到底是什么呢？我们就来解开他的神秘面纱。对于上面三硬币的例子，我们首先选取参数的初值\(\theta^{(0)}=(\pi^{(0)},p^{(0)},q^{(0)})\)，初值可以凭经验指定也可以任意设置，但是我们知道EM算法是初值敏感的，之后我们会看到到底影响多少。设置完初值后，就可以经过下面的步骤进行迭代计算参数的估计值，直至收敛为止。第i次的迭代参数的估计值为\(\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})\)，那么第i+1次的迭代如下：（这里不懂没关系，我们会稍微继续解释一下）
E步：计算模型参数下观测数据来自掷硬币B的概率：

\[\mu^{(i+1)}=\frac{\pi^{(i)} {p^{(i)}}^{y_i}(1-p^{(i)})^{1-y_i}}{\pi^{(i)} {p^{(i)}}^{y_i}(1-p^{(i)})^{1-y_i}+(1-\pi^{(i)}){q^{(i)}}^{y_i}(1-q^{(i)})^{1-y_i}} \tag{6} \]

M步：计算模型参数的新估值

\[\pi^{(i+1)}=\frac{1}{n}\sum_{j=1}^{n}\mu^{(i+1)} \tag{7} \]

\[p^{(i+1)}=\frac{\sum_{j=1}^{n}\mu^{(i+1)}y_j}{\sum_{j=1}^{n}\mu^{(i+1)}} \tag{8} \]

\[q^{(i+1)}=\frac{\sum_{j=1}^{n}(1-\mu^{(i+1)})y_j}{\sum_{j=1}^{n}(1-\mu^{(i+1)})} \tag{9} \]

看到这里，我有点懵圈，刚才还好好的，怎么经过这一迭代就这样了，内心是这样的：

[图来自网络，侵删]

其实上面只是简单介绍了下求解问题的目标函数的具体来源，而开始解这个问题时，用到EM算法部分就很快结束了，有耐心的同学可能一步一步把中间的理解步骤补全，也能跨过这个大步子，我...能怎么办...。我们在这里稍微解释下这里是如何添细节的吧：
在E步的公式（6）中，我们计算了来自的掷硬币B的概率，为什么要算这个？？？我们从EM算法的两步一步一步来看：

1. E步是算期望，那算谁的期望？当然是算未知变量，这里未知变量就是\(\mu\)（物理含义是当时到底掷的那个硬币B还是C）。啊？为什么是未知变量？
2. 至于为什么要算未知变量的期望？因为我们想让我们观测的数据的概率最大，那我们肯定要知道当时是掷哪个硬币吧？只有这样，我才能按照掷硬币B的概率分布或者掷硬币C的概率分布，把观测的结果出现的概率分布乘起来（乘起来是因为第二步中不同次的掷硬币是独立的），然后让这个概率最大（最大似然思想）。那么失望的是我不知道当时掷的是哪个硬币啊？那怎么办，那就算个期望吧！！！这样能较为合理的估计当时到底是选择了硬币B还是硬币C。
3. 知道了要算和为什么要算期望，那了解下怎么算期望？我需要一个模型的参数来算，可是我就是想通过这个来计算模型参数啊，我要是知道模型参数还在这里废这个劲干什么？这就比较尴尬了，死锁！完犊子了。那总要打破下僵局吧，那我先“随便”设置一个模型参数（在E步中模型参数的初始值），拿这组参数来计算期望。
4. 那都知道这样算出来肯定不准，现在我们总算用某种看起来比较合理的计算过程获得了一个未知变量的值。此时，如果仅仅按照值的合理程度，期望的值肯定要比“随便”设置模型参数的更为合理一些。那何不拿着个更为合理的值替代原来的未知变量的期望值，再来极大化观测变量的似然函数，计算下（更新下）模型参数（开始M步）。一算，便有了模型参数的结果。至此EM算法的第一次计算结束了，我们有了一个计算出来的期望值和计算出来的模型参数。
5. 诶？可是模型参数跟刚才“随便”设置的不一样诶。我们暂且认为这个模型参数比刚才“随便”设置的合理（之后可以证明），那么现在我又获得了更为合理的模型参数，我们再来计算下未知变量的期望值吧。一算，又跟刚才的不一样。那就重复再计算模型参数...然后，再再重新计算期望值...就这样重复又重复，直到某个时刻两个值都不怎么变了（满足停止条件），皆大欢喜，大家（模型参数和未知变量）都不用变了，好开心，停止吧。
6. 至此，EM算法也就结束了。

其实到这里，希望你对EM算法有了简单的认识，EM算法就是E步+M步；E步大概是做什么的，M步大概是做什么的。但是更希望你能有新的问题，就是你这两来回收敛我可以接受，但是这里不就是多了一个隐含变量么？管他那么多干什么，什么迭代、收敛，我可是学过偏导的人，给它们来个偏导套餐，统统求导，令导数等于0，就是干！那么你真是对力量一无所知！我们来解释下为啥要迭代求解，有什么困难：
其实我们要求的目标函数是这样一个形式，为了清晰，我们加了中括号和颜色，来清晰的显示log函数的范围：

\[L(\theta) =logP(Y|\theta) =log\sum_Z{logP(Y,Z|\theta)} =log(\sum_Z{P(Y|Z,\theta)P(Z|\theta)}) \tag{10} \]

可以看到，这里是log中是函数的和的形式，求起来很复杂，不信你想象一下\(f(x)=log(f_1(x)+f_2(x)+...+f_n(x))\)导数。嗯！就是因为这个！

至此，我们借着一篇参考文献中的图来解释下上面那个公式（6）到公式（8）了。这里跟上文的例子不太一致，建议看下原文"What is the expectation maximization algorithm？"。为了与本文的变量名匹配，我把图中的变量名称做了改动，首先看下图：

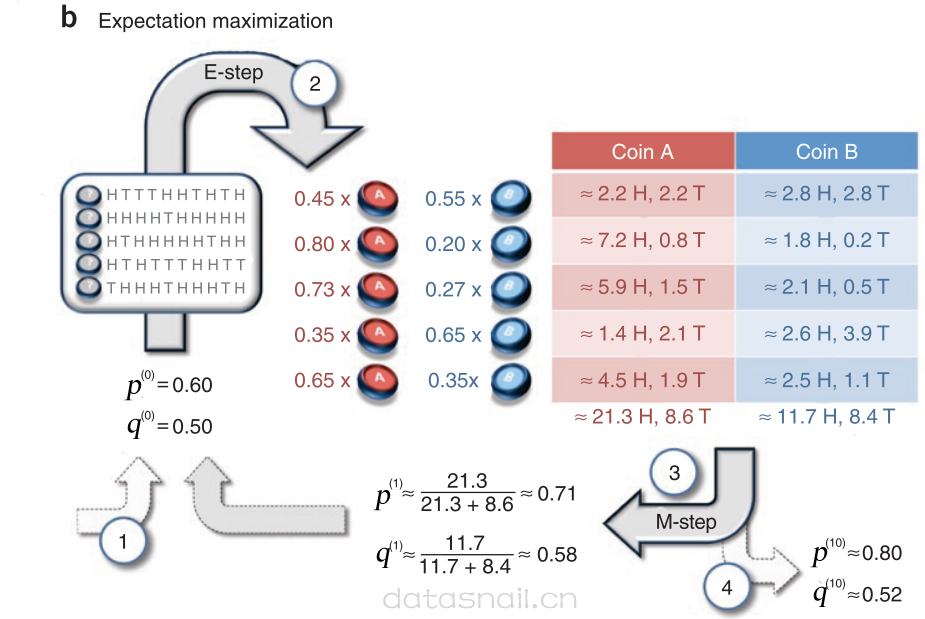
首先来看公式（6），公式（6)就是E步，在我们给了参数的初始值后，也就是上图的第①步，不同的是上图只给了两个硬币掷正面的概率，个人理解觉得这边应该是给了\(\pi=0.5\)；当赋完初值后，我们就开始根据已知数据，计算E步了（图中②步），我们计算第一组给定的数据（这里给了很多组数据）是抛硬币A出现的还是抛硬币B出现的。我们就用给定的初值计算下第一组，第一组出现5次正面，5次反面，那么如果是投掷硬币A出现的序列，那么此序列出现概率应该是\(PA=(1/2)*0.6^5*0.4^5\)，而如果是硬币B投掷出现的序列，那么此序列出现的概率应该是\(PB=(1/2)*0.5^5*0.5^5\)，我们把这两个概率归一化，即得到图中第一个序列在硬币A、B上的可能了，\(\pi_{1,A}=0.45,\pi_{1,B}=0.55\)，也就是说这个序列，更有可能是硬币B抛出来的。但是这里给了两个硬币概率（权重），那么按照这个权重可以重新算下这个序列给A、B贡献的正反面次数，而使用MLE重新计算p和q（第③步）；而有了p和q，又可以重新从①开始，直到收敛，到第④步结束。

至此，可以看到EM的大致思想了，用初值计算期望，用隐含变量的期望作为已知，用MLE计算参数，从而结束了MLE不能计算具有隐含参数的问题的历史。到现在也算是能对EM算法理解到第一层了吧。

之后，我们重新重新审视下EM算法，我们在下一节EM算法之二--算法简介继续来讲。