【深究系列】LRU算法设计

【深究系列】LRU算法设计

一、LeetCode算法题目

https://leetcode-cn.com/problems/lru-cache/

所谓缓存，必须要有读写两个操作，按照命中率的思路考虑，写操作+读操作的时间复杂度都需要O(1)

特性要求：

必须要有顺序之分，以区分最近使用的和很久没有使用的数据排序

写和读操作一次搞定。

如果容量满了要删除最不常用的数据，每次新访问还要把新的数据插入到队头（按照业务你自己设定左右哪一边是队头）

查找快、插入块、删除快，且还需要先后排序？——什么样的数据结构可以满足这个问题？

二、LRU算法核心

LRU的算法核心是哈希链表

本质就是HashMap + DoubleLinkedList，哈希表+双向链表的结合体。

查找用哈希，增删用链表。

三、巧用LinkedHashMap完成

1、参考LinkedHashMap

class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;

    public LRUCache(int capacity) {
        //true,false按照读取顺序或者插入顺序
        super(capacity, 0.75f, true);
        this.capacity = capacity;
    }
    
    public int get(int key) {
        //返回key，或者-1
        return super.getOrDefault(key, -1);
    }
    
    public void put(int key, int value) {
        super.put(key, value);
    }

    //删除最老的节点的条件
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return super.size() > capacity;
    }
}

四、手写一个LRU

核心思想

完整代码

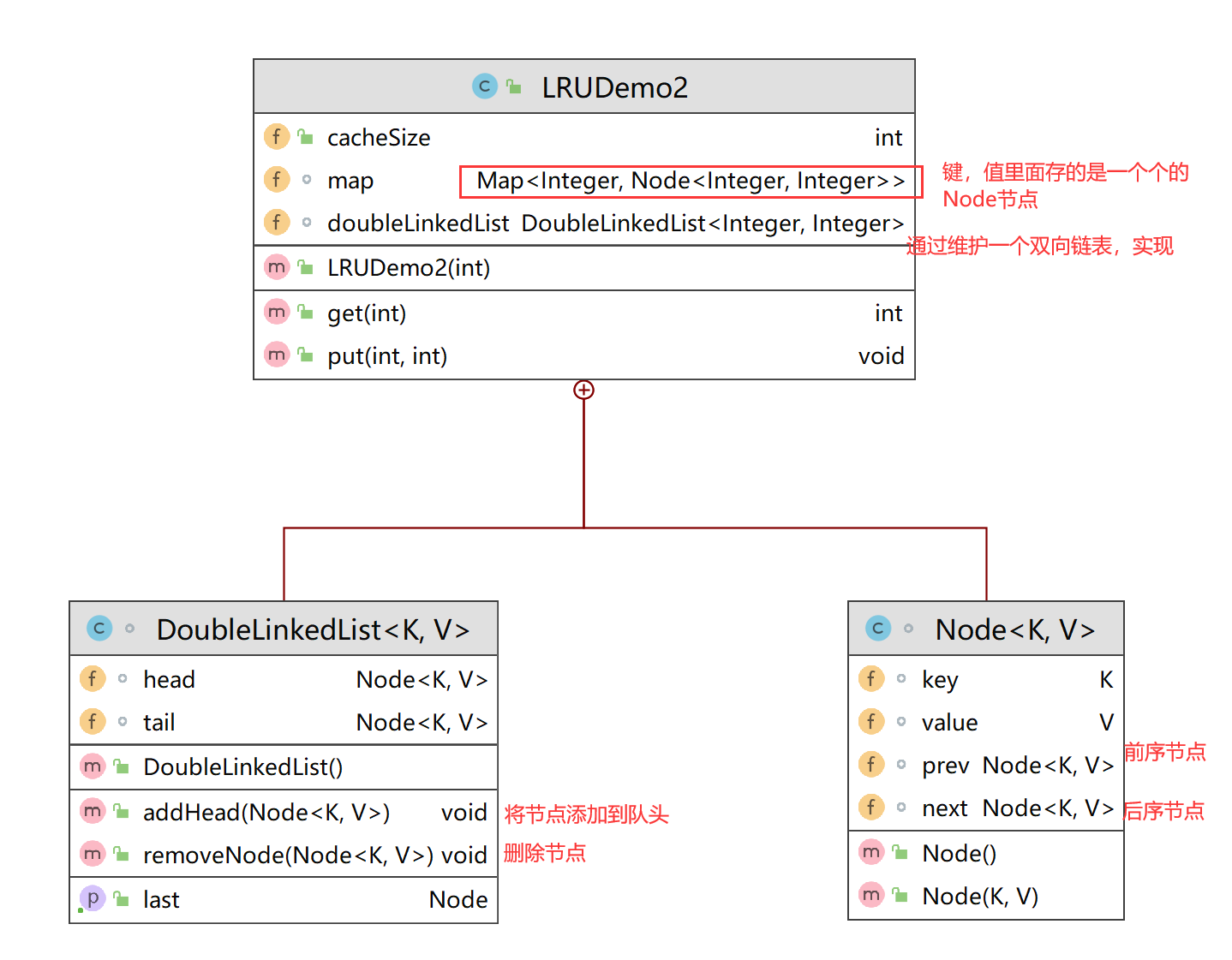
import java.util.HashMap;
import java.util.Map;

public class LRUDemo2 {
    //map负责查找，构建一个虚拟的双向链表，它里面安装的就是一个个Node结点
    //作为数据载体

    //1.构造一个Node节点，作为数据载体
    class Node<K, V>{
        K key;
        V value;
        Node<K, V> prev;
        Node<K, V> next;

        public Node() {
            this.prev = this.next = null;
        }

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.prev = this.next = null;
        }
    }

    //2. 构建一个虚拟的双向链表，里面安放的就是我们的Node
    class DoubleLinkedList<K, V> {
        Node<K, V> head;
        Node<K, V> tail;

        //2.1构造方法
        public DoubleLinkedList() {
            head = new Node<>();
            tail = new Node<>();
            head.next = tail;
            tail.prev = head;
        }

        //2.2添加到头
        public void addHead(Node<K, V> node) {
            node.next = head.next;
            node.prev = head;
            head.next.prev = node;
            head.next = node;
        }

        //2.3 删除节点
        public void removeNode(Node<K, V> node) {
            node.next.prev = node.prev;
            node.prev.next = node.next;
            node.prev = null;
            node.next = null;
        }

        //2.4 获得最后一个节点
        public Node getLast() {
            return tail.prev;
        }
    }

    public int cacheSize;
    Map<Integer, Node<Integer, Integer>> map;
    DoubleLinkedList<Integer, Integer> doubleLinkedList;

    public LRUDemo2(int cacheSize) {
        this.cacheSize = cacheSize;//坑位
        map = new HashMap<>();//负责查找
        doubleLinkedList = new DoubleLinkedList<>();
    }

    public int get(int key) {
        if (!map.containsKey(key)) {
            return -1;
        }

        Node<Integer, Integer> node = map.get(key);
        doubleLinkedList.removeNode(node);//把这个结点删掉
        doubleLinkedList.addHead(node);

        return node.value;
    }

    //saveOrUpdate method
    public void put(int key, int value) {
        if (map.containsKey(key)) {
            Node<Integer, Integer> node = map.get(key);
            node.value = value;
            map.put(key, node);

            doubleLinkedList.removeNode(node);
            doubleLinkedList.addHead(node);
        } else {
            if (map.size() == cacheSize) {//坑位满了
                Node<Integer,Integer> lastNode = doubleLinkedList.getLast();
                map.remove(lastNode.key);
                doubleLinkedList.removeNode(lastNode);
            }
            //才是新增一个
            Node<Integer, Integer> newNode = new Node<>(key, value);
            map.put(key, newNode);
            doubleLinkedList.addHead(newNode);
        }
    }
}