吴恩达机器学习笔记--ex1(Python实现)
单变量的线性回归(Linear Regression with one variable)
导入所需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
读取数据
path = 'ex1data1.txt'#路径
data = pd.read_csv(path, header=None, names=['Population','Profit'])
#print(data.head())
运行结果:
| Population | Profit | |
|---|---|---|
| 0 | 6.1101 | 17.5920 |
| 1 | 5.5277 | 9.1302 |
| 2 | 8.5186 | 13.6620 |
| 3 | 7.0032 | 11.8540 |
| 4 | 5.8598 | 6.8233 |
绘制散点图
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
#plt.show()
运行结果:
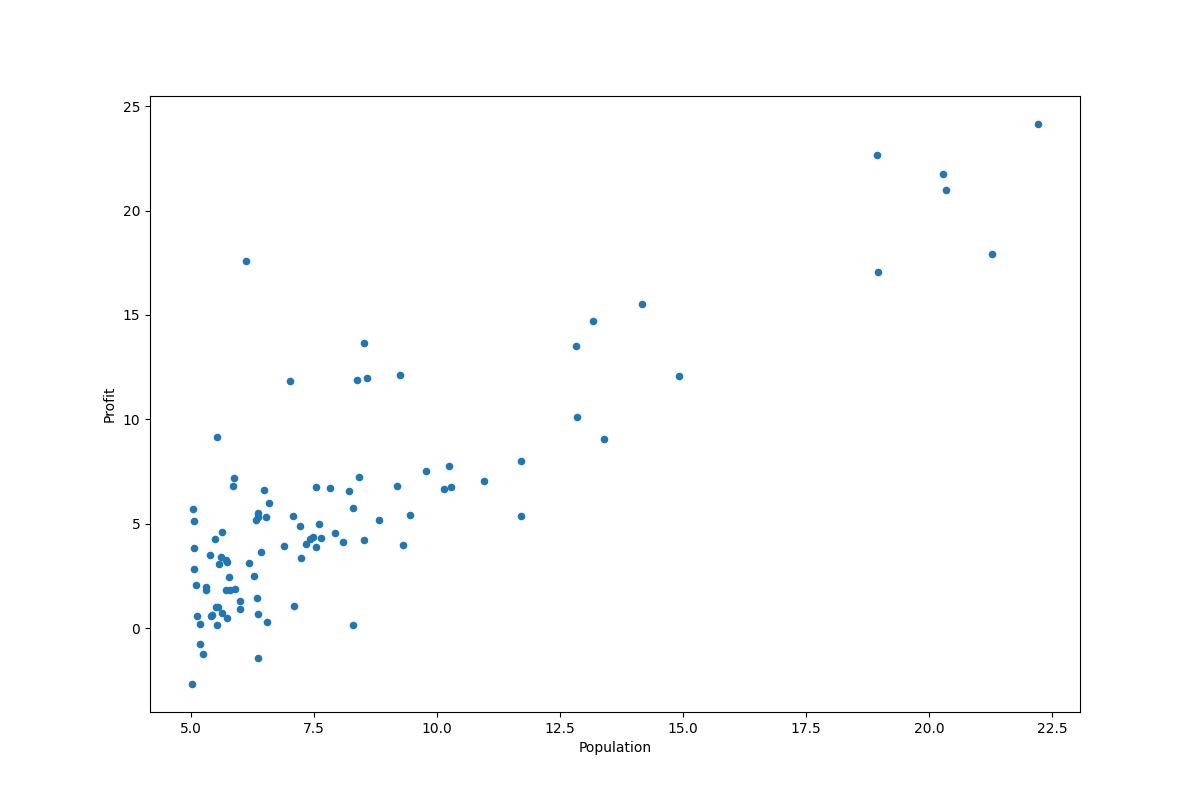
计算损失函数
\[J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
\]
其中:\(h(\theta)=\theta^TX=\theta_0x_0+\theta_1x_1+...+\theta_nx_n\) (\(n=1,x_0=1\))
len = len(data)
c = 0
theta = np.zeros(2)
t = []#t为迭代轮数
cost = []#cost为每轮的损失值
theta0 = []
theta1 = []
for j in range(len):
c += 1.0/(2*len) * pow(theta[0] * 1 + theta[1] * data.Population[j] - data.Profit[j],2)
#print(c)
运行结果:
32.072733877455676
实现梯度下降
批量梯度下降(batch gradient descent)算法的公式为:
\[\theta_j := \theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)\;\;\;\;\; (for\;i=0\;and\;i\;=1)
\]
优化:
\[\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{i}_j
\]
Correct : Simultaneous update
\[temp0:=\theta_0-\alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)
\\
temp1:=\theta_1-\alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)
\\
\theta_0:=temp0
\\
\theta_1:=temp1
\]
alpha = 0.01 #学习率
iterations = 1500 #梯度下降的迭代轮数
for i in range(iterations):
t.append(i)
temp0 = theta[0]
temp1 = theta[1]
for j in range(len):
temp0 -= (alpha/len) * (theta[0]+theta[1]*data.Population[j] - data.Profit[j])
temp1 -= (alpha/len) * (theta[0]+theta[1]*data.Population[j] - data.Profit[j]) * data.Population[j]
theta[0] = temp0
theta[1] = temp1
c = 0
for j in range(len):
c += 1.0/(2*len) * pow(theta[0] + theta[1] * data.Population[j] - data.Profit[j],2)
cost.append(c)
theta0.append(temp0)
theta1.append(temp1)
拟合
x = [5.0, 22.5]
y = [5.0 * theta[1] + theta[0], 22.5 * theta[1] + theta[0]]
plt.plot(x, y, color="red")
plt.title("Linear Regression")
plt.xlabel("Population")
plt.ylabel("Profit")
plt.scatter(data.Population, data.Profit, marker='x')
#plt.show()
运行结果:
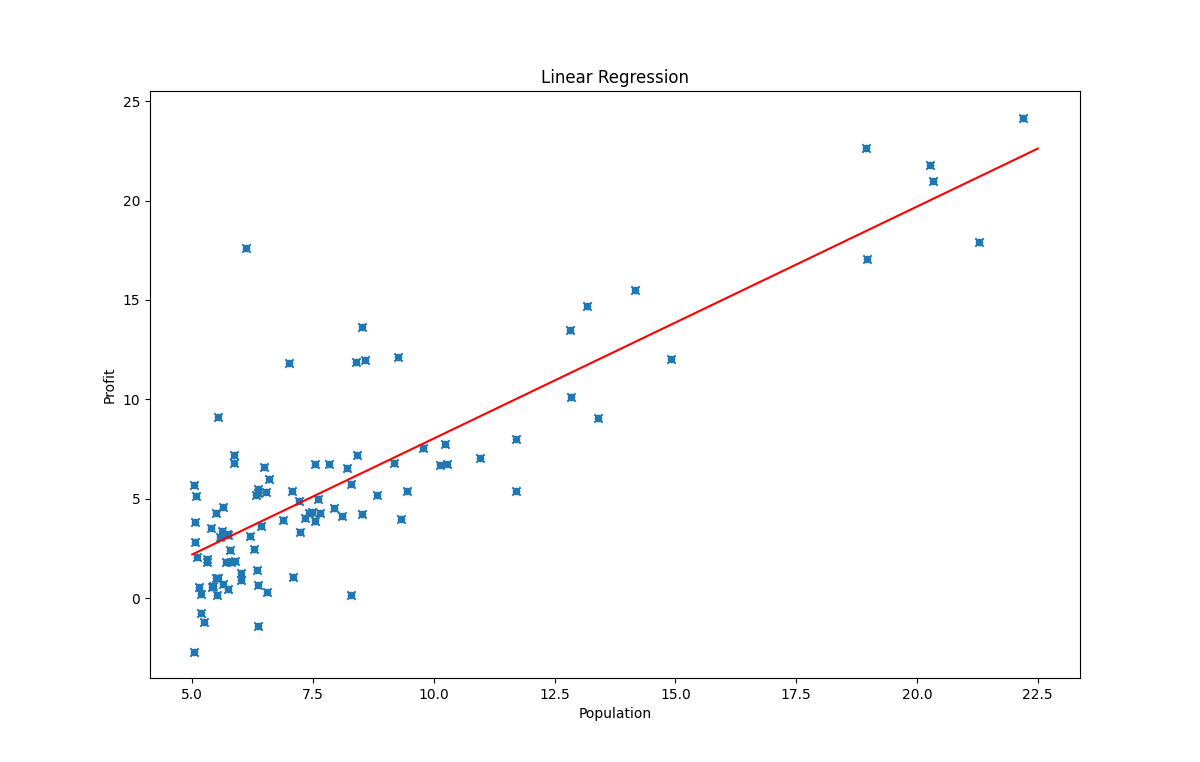
绘制损失值随梯度下降过程的变化曲线
plt.subplot(2, 2, 3)#???创建子图,subplot(nrows、ncols、index、**kwargs)
plt.title("Visualizing J(θ)")
plt.xlabel("iterations")
plt.ylabel("cost")
plt.plot(t, cost, color="red")
#plt.show()
运行结果:
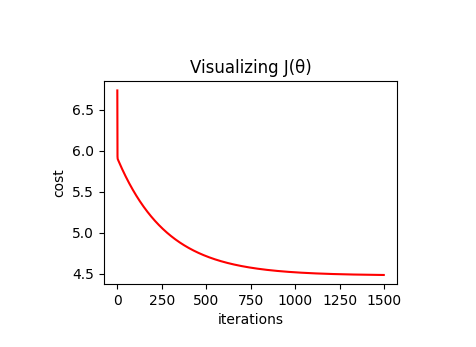
完整代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#step 1 读数据
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population','Profit'])
#print(data.head())
#step 2 绘制散点图
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
#plt.show()
#step 3 计算损失函数
len = len(data)
c = 0
theta = np.zeros(2)
t = []#t为迭代轮数
cost = []#cost为每轮的损失值
theta0 = []
theta1 = []
for j in range(len):
c += 1.0/(2*len) * pow(theta[0] + theta[1] * data.Population[j] - data.Profit[j],2)
#print(c)
#step 4 实现梯度下降
alpha = 0.01 #学习率
iterations = 1500 #梯度下降的迭代轮数
for i in range(iterations):
t.append(i)
temp0 = theta[0]
temp1 = theta[1]
for j in range(len):
temp0 -= (alpha/len) * (theta[0]+theta[1]*data.Population[j] - data.Profit[j])
temp1 -= (alpha/len) * (theta[0]+theta[1]*data.Population[j] - data.Profit[j]) * data.Population[j]
theta[0] = temp0
theta[1] = temp1
c = 0
for j in range(len):
c += 1.0/(2*len) * pow(theta[0] + theta[1] * data.Population[j] - data.Profit[j],2)
cost.append(c)
theta0.append(temp0)
theta1.append(temp1)
#step 5 拟合
x = [5.0, 22.5]
y = [5.0 * theta[1] + theta[0], 22.5 * theta[1] + theta[0]]
plt.plot(x, y, color="red")
plt.title("Linear Regression")
plt.xlabel("Population")
plt.ylabel("Profit")
plt.scatter(data.Population, data.Profit, marker='x')
#plt.show()
#step 6 绘出损失值随梯度下降过程的变化曲线,这个计算要插入到梯度下降过程中,计算和记录内容见step 4
plt.subplot(2, 2, 3)#???创建子图,subplot(nrows、ncols、index、**kwargs)
plt.title("Visualizing J(θ)")
plt.xlabel("iterations")
plt.ylabel("cost")
plt.plot(t, cost, color="red")
#plt.show()
多变量的线性回归(Linear Regression with multiple variables)
导入所需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
读取数据
path = 'ex1data2.txt'#路径
data = pd.read_csv(path , header=None , names=['house_size','bedroom_number','house_price'])
#print(data.head())
特征归一化
这里使用归一化方法的是min-max标准化,将数据映射到[-1,1]
\[x_{normalized}=\frac{x-mean}{ptp},mean=average,ptp=max−min
\]
x1 = np.array(data.house_size).reshape(-1,1) #数组新的shape属性应该要与原来的一致,如果等于-1的话,那么Numpy会根据剩下的维度计算出数组的另外一个shape属性值。
x2 = np.array(data.bedroom_number).reshape(-1,1)
y = np.array(data.house_price).reshape(-1,1)
data = np.concatenate((x1,x2,y),axis=1) #放在一个np array中便于归一化处理
#print(data)
mean = np.mean(data,axis=0)#axis=0 按列
ptp = np.ptp(data,axis=0)
nor_data = (data-mean)/ptp
X = np.insert(nor_data[..., :2], 0, 1, axis=1) #axis=1 按行添加x0=1 #nor_data[..., :2]????????
y = nor_data[...,-1]
定义损失函数
def cost(X,theta,y):
m = X.shape[0]
temp = X.dot(theta) - y
return temp.T.dot(temp) / (2 * m)
定义梯度下降函数
def gradient_descent(X, theta, y, alpha, iterations):
m = X.shape[0]
c = [] # 存储计算损失值
for i in range(iterations):
theta -= (alpha / m) * X.T.dot(X.dot(theta) - y)
c.append(cost(X, theta, y))
return theta, c
梯度下降
theta = np.zeros((3,))
alpha = 0.1
iterations = 10000
theta, c = gradient_descent(X, theta, y, alpha=alpha, iterations=iterations)
正规方程求解
\[\theta=(X^TX)^{-1}X^Ty
\]
推荐使用numpy.linalg.pinv()求矩阵的逆
def normal_equation(X,y):
return np.linalg.pinv(X.T.dot(X)).dot(X.T).dot(y)
结果比较
print("use gradient descent:", theta)
print("use normal equation", normal_equation(X,y))
运行结果:
use gradient descent: [-2.37841661e-17 9.52411131e-01 -6.59473033e-02]
use normal equation [-2.08166817e-17 9.52411140e-01 -6.59473141e-02]
损失值变化曲线
plt.title("Visualizing J(θ)")
plt.xlabel("iterations")
plt.ylabel("cost")
plt.plot([i for i in range(iterations)], c, color="red")
#plt.show()
运行结果:
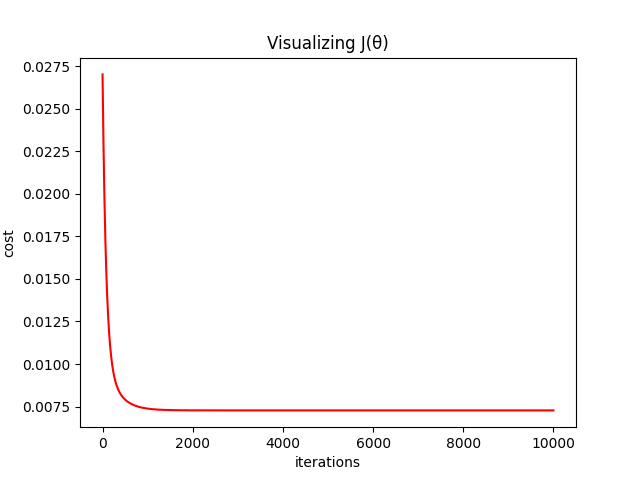
完整代码
from os import name
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def cost(X,theta,y):
m = X.shape[0]
temp = X.dot(theta) - y
return temp.T.dot(temp) / (2 * m)
def gradient_descent(X, theta, y, alpha, iterations):
m = X.shape[0]
c = [] # 存储计算损失值
for i in range(iterations):
theta -= (alpha / m) * X.T.dot(X.dot(theta) - y)
c.append(cost(X, theta, y))
return theta, c
#正规方程求解
def normal_equation(X,y):
return np.linalg.pinv(X.T.dot(X)).dot(X.T).dot(y)
path = 'ex1data2.txt'
data = pd.read_csv(path,header=None,names=['house_size','bedroom_number','house_price'])
#print(data.head())
#特征归一化
x1 = np.array(data.house_size).reshape(-1,1)
x2 = np.array(data.bedroom_number).reshape(-1,1)
y = np.array(data.house_price).reshape(-1,1)
data = np.concatenate((x1,x2,y),axis=1) #放在一个np array中便于归一化处理
#print(data)
mean = np.mean(data,axis=0)#axis=0 按列
ptp = np.ptp(data,axis=0)
nor_data = (data-mean)/ptp
X = np.insert(nor_data[..., :2], 0, 1, axis=1) #axis=1 按行添加x0=1 #nor_data[..., :2]????????
y = nor_data[...,-1]
#梯度下降
theta = np.zeros((3,))
alpha = 0.1
iterations = 10000
theta, c = gradient_descent(X, theta, y, alpha=alpha, iterations=iterations)
#使用梯度下降和正规方程所求结果有所差异
print("use gradient descent:", theta)
print("use normal equation", normal_equation(X,y))
# 损失值变化曲线
plt.title("Visualizing J(θ)")
plt.xlabel("iterations")
plt.ylabel("cost")
plt.plot([i for i in range(iterations)], c, color="red")
#plt.show()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号