图论
前言
作者大一选修了校内的图论课,经过约一个月的学习愈发感觉书中内容有趣而不失深度。
内容基于《图论导引(许胤龙、吕敏、李永坤主编)》。
但由于书中记号与定义与 OI 中相差过大,且部分课后习题富有难度,遂对其中内容做一些讨论,供大家参考。
证明时会尽量保证严谨性,但可能不能保证记号与书中相同,如有错误还望指出。
习题太过简单的可能不会写,如果有问题或者疑问可以在评论区催我写。
注:习题解答请勿盗用,谢谢支持。
图的基本概念
图的定义
定义 \(1.1\) 一个无向图 \(G\) 是一个有序三元组 \(G=(V(G),E(G),\psi_G)\),其中:
- \(V(G) \ne \varnothing\) 是顶点集合,任给 \(v \in V(G)\) 称为一个顶点。
- \(E(G)\) 是边集合,任给 \(e \in E(G)\) 称为一条边。
- \(\psi_G:E(G) \rightarrow \{\{u,v\}|u,v \in V(G)\}\) 称为边与顶点之间的关联函数。
图 \(G\) 的顶点个数 \(|V(G)|\) 称为图 \(G\) 的阶,记为 \(\nu(G)\)。图 \(G\) 的边数 \(|E(G)|\) 记为 \(\varepsilon(G)\)。若 \(\nu(G)+\varepsilon(G)\) 为无穷大,则称 \(G\) 为无限图,否则称 \(G\) 为有限图。
上述记号可以简记为 \(V,E,\nu,\varepsilon,\psi\)。
在图 \(G\) 中,若 \(\psi_G(e)=\{u,v\}\),则称 \(e\) 与 \(u,v\) 关联,也称 \(u,v\) 是 \(e\) 的两个端点;称 \(u,v\) 相邻或 \(u,v\) 是邻顶。若两条边关联同一个顶点,则称这两条边相邻。若 \(\psi_G(e)=\psi_G(f)=\{u,v\}\),则称 \(e=f\) 是重边;若 \(u=v\),则称 \(e\) 为环。
无环也无重边的图叫做简单图,一般无特指的图均为简单图。
为了方便,将 \(\psi_G(e)=\{u,v\}\) 简记为 \(e=\{u,v\}\),更进一步地,简记为 \(e=uv\),由于在无向图中,有 \(uv=vu\)。为了方便,直接记 \(G=(V,E)\),\(E\) 直接用二元顶点对的方式表示。
以下是一些特殊图:
- 完全图 \(n\) 个顶点的无向简单图 \(K_n\) 满足 \(\forall u,v \in V,u \ne v,uv \in E\)。
- 二分图 无向图 \(G\) 可以划分为 \(X \cup Y = G\),其中 \(X,Y \ne \varnothing,X \cap Y = \varnothing\),\(\forall uv \in E\),\(u,v\) 在 \(X,Y\) 中的不同集合。完全二分图 \(K_{|X|,|Y|}\) 是一个简单图,满足 \(\forall x \in X,y \in Y\) 满足 \(xy \in E\)。
- 星图 完全二分图 \(K_{1,n}\) 或 \(K_{n,1}\)。
- 零图 \(|E|=0\)。
顶点度数
定义 \(1.2\) 给定无向图 \(G\),\(v \in V\) 是 \(G\) 的一个顶点,\(v\) 的度数 \(\deg(v)\) 定义为 \(\deg(v)=d_1(v)+2 \times l(v)\),其中 \(d_1(v)\) 为 \(v\) 关联的非环边数,\(l(v)\) 为 \(v\) 关联的环边数。
定义 \(\delta(G)=\min\limits_{v \in V}\{\deg(v)\}\),\(\Delta(G)=\max\limits_{v \in V}\{\deg(v)\}\)。
将图 \(G\) 中所有顶点的度数按照从大到小的顺序排列,称为图 \(G\) 的度数序列。
定理 \(1.1(\text{Euler},1736)\) 任给无向图 \(G\),\(\sum\limits_{v \in V} \deg(v)=2\varepsilon\)。
证明
考虑 \(uv \in E\),每条边在 \(u,v\) 各贡献一次度数,按边计算总贡献为 \(2\varepsilon\),按点计算总贡献为 \(\sum\limits_{v \in V} \deg(v)\)。
推论 \(1.1\) 任给图 \(G\),\(G\) 中度数为奇数的顶点个数为偶数。
证明
记 \(G\) 中读书为奇数的顶点个数为 \(\nu_o\)。
有 \(\nu_o \equiv \sum\limits_{v \in V} \deg(v) \equiv 2\varepsilon \equiv 0 \pmod 2\)。
子图与图的运算
定义 \(1.3\) 给定图 \(G\) 与 \(H\),若 \(V(H) \subseteq V(G)\) 且 \(E(H) \subseteq E(G)\),则称 \(H\) 是 \(G\) 的一个子图,记为 \(H \subseteq G\)。
定义 \(1.4\) 一些特殊子图:
- 真子图 \(H \subseteq G\) 且 \(H \ne G\),则称 \(H\) 是 \(G\) 的真子图,\(H \subset G\)。
- 生成子图 \(H \subseteq G\) 且 \(V(H) = V(G)\),则称 \(H\) 是 \(G\) 的生成子图。
- 顶点导出子图 设 \(V' \subseteq V\),由 \(V'\) 导出的子图 \(G'[V']=(V',E')\),其中 \(E'=\{uv|u,v \in V'\}\)。
- 边导出子图 设 \(E' \subseteq E\),由 \(E'\) 导出的子图 \(G'[E']=(V',E')\),其中 \(V'=\{v|v \in V,\exist uv \in E'\}\)。
定义 \(1.5\) 补图和边图:
- 补图 图 \(G\) 的补图定义为 \(G^c=(V^c,E^c)\),其中 \(V^c=V,E^c=\{uv|u,v \in V,uv \notin E\}\)。
- 边图 图 \(G\) 的边图定义为 \(L(G)=V(L(G)),E(L(G))\),其中 \(V(L(G))=E(G)\),\(E(L(G))=\{e_1e_2|e_1,e_2\in E(G),e_1e_2 \text{ 在 } G \text{ 中相邻}\}\)。
对于 \(G\) 中的点 \(v\) 和边 \(e\),定义 \(G-v=(V-v,E-\{uv|u \in V,uv\in E\})\),\(G-e=(V,E-e)\)。
定义 \(1.6\) 两张图的并、交和积:
- 并 \(G \cup H = (V(G) \cup V(H),E(G) \cup E(H))\)。
- 交 \(G \cap H = (V(G) \cap V(H),E(G) \cap E(H))\)。
- 积 \(G \times E = (V',E')\),其中 \(V'=V(G) \times V(H) = \{(u,v)|u \in V(G),v \in V(H)\}\),\(E'=\{(u_1,v_1)(u_2,v_2)|(u_1=u_2 \land v_1v_2 \in E(H)) \lor (u_1u_2 \in E(G) \land v_1=v_2) \lor (u_1u_2 \in E(G) \land v_1v_2 \in E(H)) \}\)。
路径与连通
定义 \(1.7\) 基本概念:
- 路径 图 \(G\) 的路径 \(W\) 定义为 \(W=v_0e_1v_1e_2v_2 \cdots e_kv_k\),其中 \(v_i \in V,e_i \in E,e_i=v_{i-1}v_i\),称 \(k\) 为 \(W\) 的长度,\(v_0\) 和 \(v_k\) 分别为 \(W\) 的起点和终点。
- 行迹 边不重复的路径。
- 轨道 顶点不重复的路径。
- 回路 起点与终点相同的路径。
- 圈 除了起点和终点,没有相同顶点的回路。
若 \(u,v\) 之间存在路径,称 \(u\) 和 \(v\) 连通,否则称 \(u\) 和 \(v\) 不连通。记距离 \(\text{dist}(u,v)\) 表示 \(u,v\) 之间最短轨道的长度。特别地,若 \(u,v\) 不连通,\(\text{dist}(u,v) = \infty\)。若 \(G\) 的任意两个顶点都连通,则称 \(G\) 连通。
定义 \(1.8\) 给定图 \(G\),定义 \(V\) 上的二元关系 \(R \subseteq V \times V\) 如下:任给 \(u,v \in V\),\((u,v) \in R\) 当且仅当 \(u,v\) 在 \(G\) 中连通。
\(R\) 是自反的、对称的与可传递的。故我们可以将 \(V\) 划分为一些等价类 \(V_1,V_2,\cdots,V_{\omega}\),使得:
\((1)\) \(\forall 1 \le i \le \omega, V_i \ne \varnothing\);
\((2)\) \(\forall 1 \le i < j \le \omega,V_i \cap V_j = \varnothing\);
\((3)\) \(\bigcup\limits_{i=1}^{\omega} V_i = V\)。
满足 \((u,v) \in R \Longleftrightarrow \exists i, u,v \in V_i\)。此时称 \(G[V_i]\) 为 \(G\) 的一个连通片,\(\omega\) 为连通片个数。
记 \(G_i=G[V_i]\),可以将每个 \(G_i\) 视为一个独立的图,且有 \(G=G_1+G_2+\cdots + G_{\omega}\)
。
定理 \(1.2\) 图 \(G\) 是二分图,当且仅当 \(G\) 中无奇圈。
证明
不妨设 \(G\) 连通,易证有奇圈 \(\Longrightarrow\) 非二分图。再对无奇圈的图利用最短轨道奇偶性证明即可,读者自证不难。
图的同构
定义 \(1.9\) 给定图 \(G\) 和图 \(H\),若存在两个一一映射:
- \(\theta: V(G) \rightarrow V(H)\)。
- \(\varphi: E(G) \rightarrow E(H)\)。
满足任意 \(e \in E(G)\),当且仅当 \(\psi_G(e)=uv\) 时,有 \(\psi_H(\varphi(e))=\theta(u)\theta(v)\),则称 \(G,H\) 同构,记作 \(G \cong H\)。
学术界普遍认为,不存在多项式时间复杂度的确定性判定同构的算法。
关于同构,有如下 \(\text{Ulam}\) 猜想,至今尚未解决。
\(\textbf{Ulam}\) 猜想 \((1929)\) 设 \(G\) 和 \(H\) 是两个图,\(\nu_G=\nu_H\),若存在映射 \(\theta\),任给 \(v \in V(G),G-v \cong H-\theta(v)\),那么 \(G \cong H\)。
与 \(\text{Ulam}\) 猜想类似,也有一个边版本的猜想,同样尚未解决,这里略过。
有向图
定义 \(1.10\) 一个有向图 \(D\) 是一个有序三元组 \(D=(V(D),E(D),\psi_D)\),其中:
- \(V(D) \ne \varnothing\) 是顶点集合,任给 \(v \in V(D)\) 称为一个顶点。
- \(E(D)\) 是边集合,任给 \(e \in E(D)\) 称为一条有向边,在不会混淆的情况下也简称为边。
- \(\psi_D:E(D) \rightarrow V(D) \times V(D)\) 称为有向边与顶点之间的关联函数。
与无向图不同的是,有向图中的边用有序对表示,而无向图的边则用二元集合来表示。若存在边 \(\psi_D(e)=(u,v)\),则称 \(u\) 是 \(e\) 的起点(或尾),\(v\) 是 \(e\) 的终点(或头),\(u\) 与 \(v\) 都称为 \(e\) 的端点。
可以简写为 \(e=(u,v)\) 或 \(e=uv\),特别地,\(uv \ne vu\)。
给定有向图 \(D\),对于顶点 \(u \in V\),定义 \(u\) 的出度 \(\deg^+(u)\) 表示以 \(u\) 为起点的边数,入度 \(\deg^-(u)\) 表示以 \(u\) 为终点的边数。
\(u\) 的度数定义为两者之和,也就是 \(\deg(u)=\deg^+(u)+\deg^-(u)\)。
定理 \(1.3\) 任给有向图 \(D\),有 \(\sum\limits_{v\in V} \deg^+(v)=\sum\limits_{v\in V} \deg^-(v)=\varepsilon\)。
与无向图类似,我们可以定义有向图中的有向路径、有向迹、有向轨道、有向回路、有向圈的概念,与无向图中相关概念的区别在于:有向路径中边的方向要求一致。
若存在 \(u\) 到 \(v\) 的有向路径,则称 \(u\) 可达 \(v\)。
最短路径问题
这里使用 \(\text{OI-wiki}\) 中的内容。
习题
\(1.1.\) \(G\) 是简单图,则有 \(\varepsilon \le \dbinom{\nu}{2}\)。
\(1.2.\) 证明或举例说明下面的结论:
\((1)\) 若 \(G \cong H\),则 \(\nu(G)=\nu(H)\) 且 \(\varepsilon(G)=\varepsilon(H)\)。
\((2)\) \((1)\) 的逆不成立。
\(1.3.\) 画出所有不同构的四个顶点的简单图。
\(1.4.\) 任何至少由两个人构成的群体中,其中有两个人,他们的朋友数一样多。
解答
反证,将朋友关系构建成一张无向图,若没有人朋友数相同,说明 \(\deg\) 互不相同,又有 \(0 \le \deg < \nu\),故度数序列为 \(0,1,\cdots ,\nu -1\),\(\nu \ge 2\)。
\(\deg=0\) 和 \(\deg= \nu -1\) 分别表示没有朋友和全是朋友,显然矛盾,故原命题成立。
\(1.5.\) \(2n(n\ge 2)\) 人中,每个人至少与其中的 \(n\) 个人认识,则其中至少有四个人,使得这四个人围桌而坐时,每个人旁边都是他认识的人。
解答
将认识关系构建成一张无向图 \(G\),若任意两人互相认识,则 \(G=K_{2n}\),显然成立。
故假设两顶点 \(u,v\) 满足 \(uv \notin E\),考虑 \(u,v\) 相邻的点的集合 \(P_u,P_v\),有 \(u,v \notin P_u \cup P_v\),故 \(|P_u \cap P_v| = |P_u| + |P_v| - (2n-2) \ge 2\)。
设 \(x,y \in P_u \cap P_v,x \ne y\),则圈 \(W_C=u(ux)x(xv)v(vy)y(yu)u\) 存在,原命题成立。
\(1.6.\) 证明两张同构的图同构(图略)。
\(1.7.\) 证明下面的结论:
\((1)\) \(\varepsilon(K_{m,n}) = mn\)。
\((2)\) 设 \(G\) 是二分图,\(\varepsilon(G) \le \dfrac{\nu^2(G)}4\)。
\(1.8.\) 设 \(G\) 是图,给定 \(V(G)\) 的非空真子集 \(V'\),记 \(k\) 为一个端点在 \(V'\) 中,另一个端点在 \(V(G) - V'\) 中的边数。若 \(V'\) 中度数为奇数的顶点数为偶数,则 \(k\) 为偶数;否则,\(k\) 为奇数。
解答
记 \(\nu_o\) 为 \(V'\) 中度数为奇数的顶点个数。
\(\left(\sum\limits_{v \in V'} \deg(v)\right)-k \equiv \nu_o - k \equiv 2\varepsilon(G[V']) \equiv 0 \pmod 2\)。
\(\nu_o \equiv k \pmod 2\)。
\(1.9.\) 每个顶点的度数都是 \(2\) 的连通图是一个圈。
解答
显然 \(\nu = 1\) 时成立。
考虑找一个 \(uv \in E\)。维护一条轨道 \(W_k=v_0e_1v_1\cdots e_kv_k\),初始 \(W_1=u(uv)v\)。
考察 \(W_k \rightarrow W_{k+1}\)。\(\deg(v_k)=2\),记与它关联的两条边为 \(uv_k,wv_k\),令 \(wv_k=v_{k-1}v_k\)。
若 \(k=\nu -1\),那么 \(u=v_0\),此时 \(W_{k+1}=v_0e_1v_1\cdots e_{k+1}v_{k+1}\),且 \(v_{k+1}=v_0\),构成一个圈。
若 \(k\ne \nu -1\),那么若 \(u=v_0\),则 \(G\) 不连通,故 \(W_{k+1}=v_0e_1v_1\cdots e_{k+1}v_{k+1}\),仍是一条轨道。
至此归纳完毕,\(G\) 是一个圈。
\(1.10.\) 证明或说明下面的结论。
\((1)\) 若 \(G^c \cong G\),则称 \(G\) 是自补图。证明:若 \(G\) 是自补图,则 \(\nu(G) \bmod 4 = 0 \lor \nu(G) \bmod 4 = 1\)。
\((2)\) 有多少个 \(\nu (G)=5\) 的自补图。
解答
\((1)\) 显然 \(\varepsilon = \dfrac{\nu(\nu -1)}4\),而 \((\nu,\nu-1)=1\),故 \(4|\nu \lor 4|(\nu-1)\)。
\((2)\) 若 \(\Delta(G) = \nu -1\),那么有 \(\delta(G^c) = 0\),若 \(G\) 自补,有 \(\delta(G) = 0\),由 \(1.4.\) 中结论,\(\delta(G) = 0\) 和 \(\Delta(G) = \nu -1\) 不能同时出现。
那么度数为 \(3\) 和度数为 \(1\) 的顶点数相同,且 \(G\) 和 \(G^c\) 都连通(之前推论),故以此分类:
- 有 \(0\) 个度数为 \(1\) 的顶点。此时 \(G\) 是一个圈,答案为 \(\dfrac{4!}2=12\)。
- 有 \(1\) 个度数为 \(1\) 的顶点。那么度数为 \(1\) 和度数为 \(3\) 的顶点中间的边只存在与 \(G\) 与 \(G^c\) 其中之一,不可能同构,答案为 \(0\)。
- 有 \(2\) 个度数为 \(1\) 的顶点。那么度数为 \(1\) 不能和度数为 \(1\) 的顶点相邻,度数为 \(3\) 和度数为 \(3\) 的顶点一定相邻,那么剩余 \(4\) 条边只能往度数 \(\le 2\) 的点上连,刚好连完,答案为 \(5 \times 6 \times 2=60\)。
总答案为 \(72\)。
\(1.11.\) 构造一个二分图 \(G\),使得 \(G\) 不与任何 \(k\) 维立方体的子图同构,其中,\(k\) 为任意正整数。
\(1.12.\) \(G\) 是简单图,\(\nu(G) \ge 4\),整数 \(n\) 满足 \(1<n<\nu(G)\)。证明:若任给 \(G\) 的 \(n\) 个顶点构成的顶点子集,其导出子图都有相同的边数,则 \(G \cong K_{\nu(G)} \lor G \cong K_{\nu(G)}^c\)。
解答
取 \(n=2\) 得证。
\(1.13.\) 任给图 \(G\),都满足 \(\delta(G) \le \dfrac{2\varepsilon(G)}{\nu(G)} \le \Delta(G)\)。
解答
\(\delta(G) \le \deg(v) \le \Delta(G)\) 得证。
\(1.14.\) 我们将图 \(G\) 中所有顶点的度数按照从大到小的顺序排列,称为图 \(G\) 的度数序列。证明:
\((1)\) \(7,6,5,4,3,3,2\) 和 \(6,6,5,4,3,3,1\) 都不是简单图的度数序列。
\((2)\) 设 \(d_1,d_2,\cdots,d_n\) 是简单图的度数序列,则 \(\sum\limits_{i=1}^n d_i\) 是偶数,且对任意 \(1 \le k \le n\),都有 \(\sum\limits_{i=1}^k d_i \le k(k-1) + \sum\limits_{i=k+1}^n \min\{k,d_i\}\)。
解答
\((1).a\) 显然 \(\Delta(G) < \nu\)。
\((1).b\) 显然 \(d_1=d_2=\nu -1\),故 \(d_i \ge 2\)。
\((2)\) 显然 \(\sum\limits_{i=1}^n d_i=2 \varepsilon\),而左式分为顶点导出子图内和外两部分,边数上限分别为 \(k(k-1)\) 和 \(\sum\limits_{i=k+1}^n \min\{k,d_i\}\)。
\(1.15.\) 任给无环图 \(G\),\(G\) 有一个生成子图 \(H\),满足:
\((1)\) \(H\) 是二分图。
\((2)\) 任给 \(u \in V(G)=V(H)\),都有 \(\deg_H(u) \ge \dfrac{\deg_G(u)}{2}\)。
解答
考虑给每个顶点 \(u\) 染色 \(c_u=0/1\),\(uv \in E(H)\) 当且仅当 \(uv \in E(G) \land c_u \ne c_v\),这样 \(H\) 是二分图。初始时 \(\forall i,c_i=0\)。
考虑调整,每次找一个顶点 \(u\) 满足 \(\deg_H(u) < \dfrac{\deg_G(u)}{2}\),若不存在则 \(H\) 是答案,否则令 \(c_u' \leftarrow \lnot c_u\),此时 \(\varepsilon' \leftarrow \varepsilon + \deg_G(u)-2\deg_H(u)>\varepsilon\)。
这样每次调整 \(H\) 的边数均增多,总会调整直到找不到 \(u\),得到答案。
\(1.16.\) 假设 \(G\) 是简单图,且 \(\delta(G)\ge k\),则 \(G\) 中有长为 \(k\) 的轨道。
解答
反证,若最长轨道长度 \(W\) 长度 \(<k\),记轨道其中之一的端点为 \(u\),由于 \(\deg(u) \ge \delta(G) \ge k\),而轨道内除 \(u\) 的顶点只有至多 \(k-1\) 个,说明 \(\exists v,uv \in E,v \notin W\),那么 \(W\) 不是最长轨道,矛盾。故原命题成立。
\(1.17.\) \(G\) 是连通图,当且仅当 \(V(G)\) 任意分成两个非空子集 \(V'\) 与 \(V(G)-V'\),总存在一条边,它的两个端点分属 \(V'\) 与 \(V(G)-V'\)。
\(1.18.\) \(G\) 是简单图,且 \(\varepsilon (G)>\dbinom{\nu (G)-1}2\),则 \(G\) 是连通图。
解答
反证,由 \(1.17.\) 结论,\(G\) 不连通当且仅当存在一个划分 \(V',V-V'\) 使得不存在 \(uv \in E,u \in V',v \in V-V'\)。
考虑任意一组划分 \(V',V-V'\),若不连通则有 \(\varepsilon \le \dbinom{|V'|}{2} + \dbinom{\nu-|V'|}{2} \le \dbinom{\nu-1}{2}\)。矛盾,故原命题成立。
\(1.19.\) 对于图 \(G\)。
\((1)\) 证明:任给 \(e \in E(G)\),都满足 \(\omega(G) \le \omega(G-e) \le \omega(G)+1\)。
\((2)\) 说明:对于图 \(G\) 的任意顶点 \(v\),用 \(G-v\) 代替 \(G-e\),\((1)\) 中的不等式未必成立。
解答
\((1)\) 考虑删边会让连通性变差,左侧得证。
右侧视为 \(G-e\) 加入了一条新边 \(e\),那么连通片个数至多减少 \(1\)。
\((2)\) 考虑删除一个星图中的一个点,连通片个数减 \(1\)。
\(1.20.\) 设 \(G\) 是连通图,且每个顶点的度数都是偶数,则 \(\omega(G-v) \le \dfrac{\deg(v)}2\)。
解答
考虑 \(G-v\) 中的每一个连通片,由 \(1.8.\) 中结论,每个连通片与 \(v\) 直接至少有两条边。故原命题显然成立。
\(1.21.\) 连通图 \(G\) 中任意两条最长的轨道都有公共顶点。
解答
反证,假设 \(W_1,W_2\) 无公共顶点且长度均为 \(l\),考虑 \(W_1,W_2\) 如何连通。假设 \(x \in W_1,y \in W_2\),\(x,y\) 之间有轨道 \(W\) 满足 \(W \cap W_1 = x,W \cap W_2 = y\)。
那么记 \(W_1\) 中距 \(x\) 较远的路径端点为 \(p\),\(W_2\) 中距 \(y\) 较远的路径端点为 \(q\),由 \(p \rightarrow x \rightarrow y \rightarrow q\) 构成的轨道长度 \(l' > \dfrac{l}{2} + \dfrac{l}{2} = l\),假设不成立。
\(1.22.\) 设 \(G\) 是简单连通图,但不是完全图。证明:\(G\) 中存在三个顶点 \(u,v,w\),使得 \(uv,vw \in E(G)\),但是 \(uw \notin E(G)\)。
解答
考虑更强的性质:在 \(G\) 的最长轨道 \(W\) 上存在 \(u,v,w\) 满足以上性质。记 \(W\) 上点集为 \(V'\)。
引理 若 \(G[V']\) 不是完全图 \(K_{|V'|}\),那么存在 \(u,v,w\)。
记 \(W=v_0e_1v_1\cdots e_kv_k\),存在 \(v_iv_j(i<j) \notin E'\)。若 \(v_{i+1}v_j \in E'\),则找到 \(v_i,v_{i+1},v_j\) 符合条件。否则 \(i \leftarrow i+1\),为相同形式的子问题,且 \(j-i\) 减小,总会到 \(j-i=2\) 找到答案。
反证,若 \(G[V']\) 是完全图 \(K_{|V'|}\),讨论。
若 \(V'=V\),不满足 \(G\) 不是完全图。
若不存在 \(V',V-V'\) 中间的连边,那么由 \(1.17.\) 结论,\(G\) 不是连通图。
故存在 \(uv \in E,u \in V',v \notin V'\),此时由于 \(G[V']\) 是完全图,存在一条任意顺序经过 \(V'\) 中所有顶点的轨道,令 \(u\) 为起点的轨道是 \(W_u\),那么 \(W'=v(vu)W_u\),仍是轨道且更长,矛盾。
综上,原命题成立。
\(1.23.\) \(G\) 是一个简单图,\(e\in E(G)\) 在一个起点与终点相同的行迹上,则 \(e\) 在一个圈上。
解答
若行迹除了首尾仍有公共点,则可以分为两个行迹,选择 \(e\) 所在的一侧即可,规模减小,总能最后变成一个圈。
\(1.24.\) \(G\) 是简单图,\(\delta(G) \ge 2\),则 \(G\) 中有长为 \(\delta(G)+1\) 的圈。
解答
\(1.16.\) 扩展结论,找到最长轨道后证明不难。
\(1.25.\) 设 \(G\) 是简单图。证明:
\((1)\) 若 \(\varepsilon(G) \ge \nu(G)\),则 \(G\) 中有圈。
\((2)\) 若 \(\varepsilon(G) \ge \nu(G)+4\),则 \(G\) 中有两个无公共边的圈。
解答
这里只证明 \(G\) 是连通图,非连通的情况容易转化,这里略过。
\((1)\) 考虑 \(G\) 是由星图加边得到的。
引理 对于图 \(G\),有 \(\nu \le \varepsilon+ \omega\),特别地,\(G\) 中无圈时有 \(\nu = \varepsilon +\omega\)。
\(\varepsilon =0\) 时有 \(\nu = \omega\),每次加边可能减少一个连通片,显然成立。
无圈时每次加边必减少一个连通片,否则成圈,显然也成立。
故无圈时有 \(\varepsilon = \nu -\omega<\nu\),也就是说 \(\varepsilon \ge \nu\) 时有圈。
\((2)\) 这里使用部分树的内容证明。
只证 \(\varepsilon = \nu +4\)。
考虑构建一颗 \(G\) 的生成树 \(T\),剩下 \(5\) 条非树边记为 \(e_1,e_2,e_3,e_4,e_5\),每条边与树上一条轨道构成一个圈。
考虑拿出 \(e_5\) 构成的圈 \(W\),将圈上点的编号逆时针命名为 \(1 \sim k\)。
考虑 \(e_1,e_2,e_3,e_4\) 构成的圈与 \(W\) 的交。
引理 树上两条轨道若边相交,则交仍是一条轨道。
在树的章节学习完成后容易证明。
考虑若 \(e_i\) 构成的圈与 \(W\) 无交,则找到答案,若有交,记录为 \(P_i,Q_i\) 的形式,表达为树上轨道的两个端点,无交的部分记为 \(L_i\)。
记 \(W_{l,r}\) 表示圈上第 \(l\) 个点到第 \(r\) 个点构成的轨道(若 \(l>r\) 表示跨过第 \(k\) 个点)。
若所有 \(P_i,Q_i\) 互不相同,那么不会出现 \(i,j\) 满足 \(P_i < P_j < Q_j < Q_i\),否则 \(L_iW_{Q_i,P_i}\) 和 \(L_jW_{P_j,Q_j}\) 构成两个边不交的圈。
故令 \(P_1 <P_2 <P_3<P_4<Q_1<Q_2<Q_3<Q_4\),那么 \(W_{P_1,P_2}L_2W_{Q_1,Q_2}L_1\) 和 \(W_{P_3,P_4}L_4W_{Q_3,Q_4}L_3\) 构成两个边不交的圈。
故存在某个 \(P_i,Q_j\) 相同。
假设 \(P_1=P_2=1\),若 \(Q_1=Q_2\),则 \(L_1L_2\) 和 \(W\) 构成两个边不交的圈(这里 \(L_1L_2\) 可能有重边,但其中可以找到一个圈)。
令 \(Q_1<Q_2\),若 \(P_3,Q_3\) 均不等于 \(1,Q_1,Q_2\) 之一,那么再令 \(P_3<Q_1<Q_2<Q_4\)(若不满足则有 \(P_i < P_j < Q_j < Q_i\))。此时 \(W_{Q_3,P_3}L_3\) 和 \(L_1L_2W_{Q_1,Q_2}\) 构成两个边不交的圈。
假设 \(P_3=1\),那么可以推断出 \(P_4=1\),且令 \(Q_1<Q_2<Q_3<Q_4\),那么 \(L_2L_3W_{Q_2,Q_3},L_1L_4W_{Q_4,Q_1}\) 和 \(L_1L_1W_{Q_1,Q_2},L_3L_4W_{Q_3,Q_4}\) 中必有一组满足条件。
故假设 \(P_3=Q_1\),那么若 \(Q_2=Q_3\),则 \(L_1L_2L_3\) 和 \(W\) 构成两个边不交的圈。
也就是说 \(Q_2<Q_3\),此时无论 \(P_4,Q_4\) 满足何种条件均会变成之前讨论过的情况之一,故无论如何均能找到两个边不交的圈。
\(1.26.\) 给定 \(G\) 的邻接矩阵表示,求单源最短路。
\(1.27.\) 船公要将一只狼、一只羊和一棵白菜运过河。假定一次只能运其中的一个,且为了安全起见,又不能使得狼与羊,或者羊与白菜在无人看管时在一起。请为船公设计一个安全快速的运送方案。
解答
羊 \(\rightarrow\) 空 \(\leftarrow\)。
狼 \(\rightarrow\) 羊 \(\leftarrow\)。
菜 \(\rightarrow\) 空 \(\leftarrow\)。
羊 \(\rightarrow\)。
\(1.28.\) 现有一个 \(8\) 升的瓶子,其中装满酒。给你两只容量分别为 \(3\) 升与 \(5\) 升的空瓶子,请设计一个将 \(8\) 升酒平分为两个 \(4\) 升的方法。
解答
\(8 \rightarrow 5,8(3),5(5),3(0)\)。
\(5 \rightarrow 3,8(3),5(2),3(3)\)。
\(3 \rightarrow 8,8(6),5(2),3(0)\)。
\(5 \rightarrow 3,8(6),5(0),3(2)\)。
\(8 \rightarrow 5,8(1),5(5),3(2)\)。
\(5 \rightarrow 3,8(1),5(4),3(3)\)。
\(3 \rightarrow 8,8(4),5(4),3(0)\)。
\(1.29.\) 假设 \(G\) 是连通图,\(\nu(G)\ge 2\) 且 \(\varepsilon(G)< \nu(G)\),则 \(G\) 中至少有两个度数为 \(1\) 的顶点。
解答
利用 \(1.25.\) 中引理证明难度不大,留给读者思考。
树
树的基本概念
定义 \(2.1\) 连通无圈图称为树,用 \(T\) 表示。树中度数为 \(1\) 的顶点称为树叶,度数大于 \(1\) 的顶点称为分支点,边称为树枝。每个连通片都是树的非连通图称为森林。孤立点称为平凡树。
定理 \(2.1\) 设 \(G=(V(G),E(G))\) 是简单无向图,则以下命题等价:
- \(G\) 是树。
- \(G\) 的任意两个顶点之间有且仅有一条轨道。
- \(G\) 不含圈,且 \(\varepsilon(G)=\nu(G)-1\)。
- \(G\) 是连通图,且 \(\varepsilon(G)=\nu(G)-1\)。
- \(G\) 是连通图,且删去任意一条边后都不连通。
- \(G\) 不含圈,且任意添加一条边后恰好含一个圈。
断言 若 \(G\) 是连通图,则 \(\varepsilon(G) \ge \nu(G)-1\)。
定理 \(2.2\) 任一非平凡树 \(T\) 至少有两片树叶。
证明
\(\nu >1\),而 \(T\) 连通,故 \(\delta(T)\ge 1\),记 \(\deg(v)=1\) 的 \(v \in V\) 有 \(k\) 个,那么有 \(2\varepsilon=2\nu-2 \ge 2(\nu-k)+k=2\nu -k\),得到 \(k \ge 2\)。
定义 \(2.2\) 设图 \(G=(V,E)\) 是连通图,任取 \(v \in V\),称 \(l(v)=\max\{\text{dist}(u,v)|u \in V\}\) 是顶点 \(v\) 的离心率,称 \(r(G)=\min\{l(v)|v \in V\}\) 是图 \(G\) 的半径。
离心率恰好等于半径(即 \(l(v)=r(G)\))的顶点 \(v\),称为 \(G\) 的一个中心点,\(G\) 中全体中心点的集合称为 \(G\) 的中心。
生成树
定义 \(2.3\) 如果图 \(G\) 的生成子图 \(T\) 是树,则称 \(T\) 是 \(G\) 的一棵生成树;如果 \(T\) 是森林,称它为 \(G\) 的生成森林。生成树的边称为树枝,图 \(G\) 中非生成树的边称为弦。\(T\) 相对于 \(G\) 的补图 \(T^c_G\) 称为 \(G\) 的余树。\(T^c_G\) 是 \(G\) 的生成子图,其边集合由 \(G\) 中不在 \(T\) 上的边组成。
定理 \(2.3\) 每个连通图都有生成树。
证明
\(G\) 连通,故 \(G\) 存在连通生成子图,考虑边最少的连通生成子图 \(G'\)。若 \(G'\) 含圈 \(C\),那么考虑删除 \(e \in C\),\(G'-e\) 仍为 \(G\) 的连通生成子图,\(G'\) 不是边最少的。
故 \(G'\) 不含圈,\(G'\) 是 \(G\) 的生成树。
推论 \(2.1\) 若 \(G\) 是连通图,则 \(\varepsilon(G) \ge \nu(G)-1\)。
推论 \(2.2\) \(G\) 是连通图的充分必要条件是 \(G\) 有生成树。
定理 \(2.4(\text{Cayley})\) 设 \(G\) 是连通图,\(e=uv \in E(G)\) 且不是环,则 \(\tau(G)=\tau(G-e)+\tau(G\cdot e)\),其中,\(\tau(G)\) 表示 \(G\) 的生成树数量,\(G \cdot e\) 是 \(G\) 中收缩掉边 \(e\) 后得到的图,即首先删掉边 \(e\),然后将 \(u\) 与 \(v\) 合并为一个顶点,设为 \(w\),再将 \(G\) 中原来与 \(u\) 或 \(v\) 相邻的顶点都与 \(w\) 连一条边。
证明
考虑将 \(G\) 的生成树分为包含 \(e\) 与不含 \(e\) 两类,\(\tau(G)=\tau(G-e)+\tau(G\cdot e)\)。
定理 \(2.5\) \(\tau(K_n) = n^{n-2}\)。
这里使用 \(\text{OI-wiki}\) 中的内容。
关于生成树计数,还有矩阵树定理。
这里使用 \(\text{OI-wiki}\) 中的内容。
最小生成树
定义 \(2.4\) 给定连通边权图 \(G=(V(G),E(G),w)\),其中,\(w:E(G) \rightarrow \mathbf{R} ^+\) 为边权函数,\(G\) 的生成树 \(T\) 的权定义为 \(w(T) = \sum\limits_{e \in E(T)} w(e)\),权最小的生成树称为 \(G\) 的最小生成树。
求最小生成树一般有 \(\text{Kruskal}\) 和 \(\text{Prim}\) 两种算法。
这里使用 \(\text{OI-wiki}\) 中的内容。
还有一种破圈法,由 \(\text{Rosenstiehl}\) 和管梅谷分别于 \(1967\) 年和 \(1975\) 年给出,在习题中还会遇到。
二叉树及其应用
定义 \(2.5\) 有根树是指定一个顶点作为根,并且每条边的方向都离开根的有向树。设 \(T\) 是一棵非平凡的有根树,任给 \(v_i,v_j \in V(T)\),若 \((v_i,v_j) \in E(T)\),则称 \(v_i\) 为 \(v_j\) 的父亲,\(v_j\) 是 \(v_i\) 的儿子;同父之子称为兄弟;若从 \(v_i\) 到 \(v_j\) 有一条有向轨道,则称 \(v_i\) 为 \(v_j\) 的祖先,\(v_j\) 是 \(v_i\) 的后代。
一般认为 \(v \in V(T)\) 是自己的祖先,也是自己的后代。
定义 \(2.6\) 在有根树中仅有一个顶点入度为 \(0\),其余顶点的入度均为 \(1\)。有根树 \(T\) 中入度为 \(0\) 的顶点就是根,入度为 \(1\) 出度为 \(0\) 的顶点称为树叶,入度为 \(1\) 出度不为 \(0\) 的顶点称为内点,内点和根统称为分支点。从根到 \(T\) 的任一顶点 \(v\) 的距离称为 \(v\) 的深度 \(L(v)\),深度的最大值称为树高 \(h(T)\)。
根的深度为 \(0\),称为第 \(0\) 层。深度同为 \(i\) 的顶点构成树的第 \(i\) 层。
定义 \(2.7\) 设 \(T\) 是一棵有根树,若每个顶点的孩子都从左到右规定了次序,则称 \(T\) 是有序树。
定义 \(2.8\) 设 \(T\) 是一棵有根树。
- 若 \(T\) 的每个分支点至多有 \(r\) 个儿子,则称 \(T\) 是 \(r\) 叉树。
- 若 \(T\) 的每个分支点都恰好有 \(r\) 个儿子,则称 \(T\) 是 \(r\) 叉正则树。
- 若 \(T\) 是 \(r\) 叉正则树且每个树叶的深度都是树高,则称 \(T\) 是 \(r\) 叉完全正则树。
- 若 \(T\) 是 \(r\) 叉树且为有序树,则称 \(T\) 是有序 \(r\) 叉树。
- 若 \(T\) 是 \(r\) 叉正则树且为有序树,则称 \(T\) 是有序 \(r\) 叉正则树。
- 若 \(T\) 是 \(r\) 叉完全正则树且为有序树,则称 \(T\) 是有序 \(r\) 叉完全正则树。
定理 \(2.8\) 二叉树有以下性质:
- 第 \(i\) 层的顶点数最多是 \(2i\)。
- 深度为 \(h\) 的二叉树最多有 \(2^{h+1}-1\) 个顶点。
- 设二叉树出度为 \(2\) 的顶点数为 \(n_2\),树叶数为 \(n_0\),则有 \(n_0=n_2+1\)。
- 包含 \(n\) 个顶点的二叉树的高度至少为 \(\log(n+1)-1\)。
定义 \(2.9\) 设二叉树 \(T\) 有 \(t\) 片树叶 \(v_1,v_2,\cdots,v_t\),其权值分别为 \(w_1,w_2,\cdots , w_t\),\(T\) 的加权路径长度 \(\text{(weighted path length)}\) 定义为:\(\text{WPL}(T) = \sum\limits_{i=1}^t w_iL(v_i)\),其中 \(L(v_i)\) 为 \(v_i\) 的深度。
给定一组树叶的权值,加权路径长度最短的树称为最优二叉树。最优二叉树常用于各类优化问题。
\(\text{Huffman(1951)}\) 提出了一种求最优二叉树的算法。
这里使用 \(\text{OI-wiki}\) 中的内容。
定义 \(2.11\) 决策树又称为判定树,是运用于分类的一种树结构。它的每个分支点对应输入数据的一个特征,表示对此特征的一次测试;每条边表示一个测试结果;树叶表示最终的分类结果,代表某个具体的类或者类的分布。
决策树模型形成了分类或者预测规则,可以看作一组 \(\text{if-then}\) 规则的集合,从根到叶的每一条路径代表了一条规则;可以证明,这些规则具有互斥且完备的性质,即每一个样本被且只被一条路径覆盖。
构造决策树通常采用自上而下的递归构造方法,通过不断选择特征并根据所选择的特征进行测试,使得一个分支点包含的数据尽可能属于同一个类别。
习题
\(2.1.\) 树 \(T\) 有 \(9\) 片树叶,\(3\) 个顶点度数为 \(3\),其余顶点的度数都是 \(4\),则 \(T\) 中有几个度数为 \(4\) 的顶点?你能画出多少棵非同构的无向树 \(T\)?
\(2.2.\) 一棵树 \(T\) 有 \(n_i\) 个度数为 \(i\) 的顶点,\(i = 2,3,\cdots ,k\),其余顶点都是树叶,则 \(T\) 有几片树叶?
\(2.3.\) 证明:如果一棵树只有两片树叶,则这棵树是一条轨道。
解答
考虑归纳证明。
当 \(\nu = 2\) 时,显然成立。
当 \(\nu > 2\) 时,找到 \(T\) 的一个树叶 \(v\),考虑 \(T'=T-v\)。显然 \(T'\) 也是一棵树,并且叶子数量 \(\le 2\)。
引理 对于 \(\nu \ge 2\) 的树 \(T\),至少有两个树叶。
找到 \(T\) 中最长轨道 \(W\),\(W\) 长度至少为 \(2\),端点显然 \(\deg = 1\),是树叶。
也就是说在 \(T'\) 中也有两个树叶,考虑新出现的树叶 \(u\),有 \(uv \in E(T)\),\(\deg_T(u)=2\)。
若 \(T'\) 是一条轨道,那么 \(T\) 也是一条轨道,归纳完成。
\(2.4.\) 证明:如果 \(T\) 是树,且 \(\Delta(T) \ge n\),则 \(T\) 至少有 \(n\) 片树叶。
解答
找到 \(v \in V,\deg(v) = \Delta\)。考虑 \(T-v\) 被划分为的 \(\Delta\) 个连通片 \(G_1,G_2, \cdots , G_\Delta\)。
对于每个 \(G_i\),若 \(\nu(G_i)=1\),则是平凡树,该点在 \(T\) 中是一个树叶。
若 \(\nu(G_i) \ge 2\),则至少有两个树叶,可能有一个与 \(v\) 相连,但在 \(T\) 中也有至少一个树叶。
故 \(T\) 中至少 \(n\) 个树叶。
\(2.5.\) 图 \(G\) 是森林当且仅当 \(\varepsilon=\nu-\omega\),其中 \(\omega\) 是 \(G\) 的连通片个数,\(\omega>1\)。
解答
图 \(G\) 是森林 \(\Longrightarrow \varepsilon=\nu-\omega\) 易证。
反过来对于每个连通片说明 \(\varepsilon \ge \nu -1\) 即可,必须同时取等。
\(2.6.\) 证明:树有一个中心或两个中心,且有两个中心时,这两个中心相邻。
解答
考虑找到 \(T\) 中的最长轨道 \(W=(v_1,v_2,\cdots,v_k)\)。
定义 \(\text{lca}(u,v)\) 表示 \(L(w)\) 最大的且是 \(u,v\) 共同祖先的 \(w\) 是 \(u,v\) 的最近公共祖先。
引理 对任意 \(u \in V\),\(l(u) = \max\{\text{dist}(u,v_1),\text{dist}(u,v_k)\}\)。
若 \(\text{dist}(u,w)>\max\{\text{dist}(u,v_1),\text{dist}(u,v_k)\}\),以 \(u\) 为根,将 \(T\) 定向为有根树。
考虑 \(\text{lca}(v_1,w),\text{lca}(v_2,w)\) 中深度较小的一个,不妨认为是 \(v=\text{lca}(v_1,w)\),显然 \(L(v) \le L(\text{lca}(v_1,v_k))\)。
那么 \(\text{dist}(v_1,w)=L(v_1)+L(w)-2L(v) > L(v_1)+L(v_k)-2L(\text{lca}(v_1,v_k))=\text{dist}(v_1,v_k)\),\(W\) 不是最长轨道。
以 \(v_1\) 为根,将 \(T\) 定向为有根树。对于 \(1 \le i \le j \le k\),\(v_i\) 是 \(v_j\) 的祖先。
显然对于 \(u \in V - W\),显然 \(l(u) \ge l(\text{lca}(u,v_k))\)。而 \(l(v_i)=\max\{\text{dist}(v_i,v_1),\text{dist}(v_i,v_k)\}=\max\{i-1,k-i\}\)。
所以 \(k\) 为奇数时,\(G\) 的中心为 \(\{v_{\frac{k+1}2}\}\)。\(k\) 为偶数时,\(G\) 的中心为 \(\{v_{\frac{k}2},v_{\frac{k}2+1}\}\)。
\(2.7.\) 证明:若 \(G\) 是森林,且有 \(2k\) 个度数为奇数的顶点,则 \(G\) 中有 \(k\) 条无公共边的轨道,使得 \(G\) 的每条边都在这些轨道上。
解答
显然对于每个连通片独立,只证 \(G\) 是树 \(T\) 时的情况。进行如下算法:
初始时每条边均为一个轨道,每次考虑对一个点 \(v\) 进行轨道合并的操作。
若 \(\deg (v)\) 是奇数,那么认为边是 \(e_1,e_2,\cdots,e_{2k+1}\),合并 \(e_{2i-1},e_{2i}\) 所在轨道。
若 \(\deg (v)\) 是偶数,那么认为边是 \(e_1,e_2,\cdots,e_{2k}\),合并 \(e_{2i-1},e_{2i}\) 所在轨道。
显然每次合并操作之后仍满足所有轨道边不相交且每条边恰在一条轨道上,符合条件。
合并操作共 \(\sum\limits_{v \in V} \left\lfloor \dfrac{\deg(v)}{2} \right\rfloor = \dfrac{ \sum\limits_{v \in V} \deg(v) - 2k}{2} = \varepsilon -k\),也就是说最终轨道有 \(k\) 条。
\(2.8.\) 证明:若 \(d_1 \ge d_2 \ge \cdots \ge d_{\nu}\) 是正整数序列,则此序列是树的度数序列当且仅当 \(\sum\limits^{\nu}_{i=1} d_i = 2(\nu-1)\)。
解答
显然树 \(T\) 的度数序列 \(\Longrightarrow \sum\limits^{\nu}_{i=1} d_i = 2(\nu-1)\)。
只证 \(\sum\limits^{\nu}_{i=1} d_i = 2(\nu-1) \Longrightarrow\) 是树 \(T\) 的度数序列。
考虑归纳。
引理 当 \(\nu >1\) 时,\(d_\nu =1\)。
若 \(d_\nu>1\),则 \(\sum\limits^{\nu}_{i=1} d_i \ge 2 \nu\),矛盾。
引理 当 \(\nu >2\) 时,\(d_1 \ge 2\)。
若 \(d_1 < 2\),则 \(\sum\limits^{\nu}_{i=1} d_i = \nu\),矛盾。
当 \(\nu=1\) 时,显然 \(d_1=1\) 是平凡树。
当 \(\nu=2\) 时,显然 \(d_1=d_2=1\) 是树。
当 \(\nu>2\) 时,考虑连接一条 \((1,\nu)\) 的边,这样新度数序列 \(\{d_i\}\) 仍有 \(\sum\limits^{\nu-1}_{i=1} d'_i = 2(\nu-2)\),在 \(\nu-1\) 是树的情况下 \(\nu\) 也是树,归纳完成。
\(2.9.\) 证明:设 \(G\) 是 \(\delta \ge k\) 的简单图,\(T\) 是 \(k+1\) 个顶点的树,则 \(G\) 中有与 \(T\) 同构的子图。
解答
考虑如下算法。
记录集合 \(S \subseteq V(T),P \subseteq V(G)\),以及一个映射 \(\theta : V(T) \rightarrow V(G)\)。
初始时任取 \(u_0 \in V(T),v_0 \in V(G),S=\{u_0\},P=\{v_0\},\theta(u_0)=v_0\)。
进行如下操作 \(k\) 轮,在第 \(i\) 轮时:
- 任取 \(u_i \in V(T) - S\),满足存在 \(u_j \in S,u_iu_j \in E(T)\)。
- 一定可以找到 \(v_i \in V(G) - P\),满足存在 \(u_j \in S,v_i\theta(u_j) \in E(G)\)。
- \(\theta(u_i)=v_i\),\(S \leftarrow S + u_i,P \leftarrow P + v_i\)。
只需要证明第二步最后就会得到 \(\theta\),也就能找到同构子图。
第二步证明也是简单的,显然 \(\deg_T(u_i) \le k \le \delta\),也就是说对于选出的 \(u_j\) 对应的 \(v_j=\theta(u_j)\) 一定存在 \(v_i \in V(G) - P\) 满足 \(v_iv_j \in E\)。
这样就构造出了同构子图。
\(2.10.\) 碳原子四价,氢原子一价,\(\text{C}_m\text{H}_n\) 是烷烃分子式,价键不呈回路,则对每个自然数 \(m\),仅当 \(n=2m+2\) 时,\(\text{C}_m\text{H}_n\) 才可能存在。
解答
计算度数证明,留给读者思考。
\(2.11.\) 求 \(K_{2,3}\) 生成树的个数。
解答
令 \(X=\{1,2\}\),考虑按 \(\deg(1)\) 分类。
- \(\deg(1)=3\),那么 \(\deg(2)=1\),任选一条连接即可,答案为 \(3\)。
- \(\deg(1)=2\),那么 \(\deg(2)=2\),容斥,所有方案减去成环的,答案为 \(3\times 3 - 3=6\)。
- \(\deg(1)=1\),那么 \(\deg(2)=3\),任选一条连接即可,答案为 \(3\)。
总答案为 \(12\)。
\(2.12.\) 轮 \(W_n\) 是一个 \(n\) 阶圈加上一个新顶点,把圈上的每个顶点都和新顶点之间连一条边(称为辐条)。求含有 \(n\) 个辐条的轮的生成树数目。
解答
考虑枚举新顶点连出来的边有 \(i\) 条。
那么圈上的边会选 \(n-i\) 条,将圈分为 \(i\) 段,每一段需要恰好一个顶点与新顶点连边。
考虑组合意义,枚举一条圈上没选的边,形式化的获得 \(n+i-1\) 个顶点,选其中 \(2i-1\) 个,交错的变为 \(i\) 个连向新顶点的顶点和 \(i-1\) 条圈上没选的边,完全符合一个生成树的限制。
有 \(n\) 个顶点,每个相同的生成树会被计算 \(i\) 次,故答案为 \(\sum\limits_{i=1}^n \dfrac{n}{i} \dbinom{n+i-1}{2i-1}\)。
在 \(\text{oeis}\) 上得到了一个通项公式是 \(\text{Fib}(2n-1)+\text{Fib}(2n+1)-2\),其中 \(\text{Fib}(i)=\text{Fib}(i-1)+\text{Fib}(i-2),i \ge 3\),\(\text{Fib}(1)=\text{Fib}(2)=1\)。
\(2.13.\) 证明:\(\tau(K_\nu -e) =(\nu -2)\nu^{\nu-3}\)。
解答
考虑 \(\tau(K_\nu)=\nu^{\nu-2}\),容斥掉选择 \(e\) 的那些生成树。
显然每条边对称,故其在 \(\tau(K_\nu \cdot e)=\dfrac{(\nu-1)\nu^{\nu-2}}{\nu(\nu-1)/2}=2\nu^{\nu-3}\) 棵生成树上。
\(\tau(K_\nu-e)=\tau(K_\nu)-\tau(K_\nu \cdot e)=(\nu-2)\nu^{\nu-3}\)。
\(2.14.\) 分别用 \(\text{Kruskal}\) 算法和 \(\text{Prim}\) 算法求边权图的最小生成树。
\(2.15.\) 边权图里的最小生成森林是权最小的生成森林,并且在生成森林中保持原图中任意两个顶点间的连通性。如何修改 \(\text{Kruskal}\) 算法和 \(\text{Prim}\) 算法来构造最小生成森林,并指出时间复杂度。
\(2.16.\) 关于破圈法。
\((1)\) 试给出破圈法的算法。
\((2)\) 证明:破圈法得到的生成树是最小生成树。
\((3)\) 分析破圈法的时间复杂度。
\(2.17.\) 证明:一棵有向树 \(T\) 是有根树,当且仅当 \(T\) 中有且仅有一个顶点的入度为 \(0\)。
解答
证明有根树 \(T \Longrightarrow\) 有且仅有一个顶点的入度为 \(0\) 是容易的。
考虑证明反命题,首先把入度为 \(0\) 的顶点设为根 \(u\)。
任取 \(v \in V-u\),\(u,v\) 之间存在有向轨道。
记 \(u,v\) 之间的轨道为 \(W=x_0x_1\cdots x_k\),其中 \(x_0=u,x_k=v\)。
轨道上的边的方向一定是 \((x_{i-1},x_i)\)。
考虑反证,找到最小的 \(i\) 使得边的方向是 \((x_i,x_{i-1})\),那么显然 \(i \ne 1\),否则 \(\deg^-(u) \ne 0\)。
那么 \(\deg^-(x_{i-1}) \ge 2\),而 \(\sum\limits_{v \in V-1} \deg^-(v)=\varepsilon=\nu-1\),\(\deg^-(v) \ge 1\),故 \(\deg^-(v)=1\),矛盾。
除根外其他顶点入度均为 \(1\),\(T\) 是有根树。
\(2.18.\) 设 \(T\) 是二叉正则树,\(i\) 是分支点数,\(I\) 是各分支点的深度之和,\(L\) 是各树叶的深度之和,证明:\(L=I+2i\)。
解答
二叉正则树 \(n_1=0\),故 \(n_0=n_2+1=\dfrac{\nu+1}{2}\)。
考虑用一种方式刻画 \(L-I\):将每条边记录一个权值 \(w_e\),初始为 \(0\)。
对于每个树叶,将其到根的轨道上所有边边权 \(+1\),对于每个分支点,将其到根的轨道上所有边边权 \(-1\)。这样最后 \(\sum\limits_{e \in E} w_e\) 恰好是 \(L-I\)。
考虑每条边 \(e=uv\) 的权值,令 \(u\) 是 \(v\) 的父亲,\(v\) 的子树仍是一个二叉正则树,也就是说 \(w_e=1\)。
故 \(\sum\limits_{e \in E} w_e=\nu-1=2i=L-I\)。
\(2.19.\) 设 \(T\) 是二叉正则树,有 \(t\) 片树叶,证明 \(T\) 的边数 \(\varepsilon=2t-2\)。
\(2.20.\) 画出带权 \(0.2, 0.17, 0.13, 0.1, 0.1, 0.08, 0.06, 0.07, 0.03\) 的 \(\text{Huffman}\) 树。
\(2.21.\) 用 \(\text{Huffman}\) 编码来编码具有给定频率的如下符号:\(a : 0.20, b : 0.10, c : 0.15, d : 0.25, e : 0.30\)。编码一个符号平均需要多少个二进制数字?
\(2.22.\) 证明:给定 \(w_1 \le w_2 \le \cdots \le w_t\),则存在一棵 \(\text{Huffman}\) 树,使得 \(w_1,w_2\) 对应的顶点是兄弟,且这两个顶点在二叉树中的深度都等于树高。
\(2.23.\) 证明:\(\text{Huffman}\) 树是最优二叉树。
解答
考虑一棵最优二叉树满足的要求。
不妨认为权值 \(w_1 \le w_2 \le \cdots \le w_\nu\),对应的深度为 \(L(1),L(2),\cdots,L(\nu)\),那么显然 \(L(1) \ge L(2) \ge \cdots \ge L(\nu)\)。
由 \(2.22.\) 结论,合并 \(w_1,w_2\) 为新顶点 \(w'=w_1+w_2\) 后问题规模变为 \(\nu-1\),当 \(\nu=1\) 时显然为最优二叉树,故结论成立,找到了最优二叉树所对应的某个 \(\text{Huffman}\) 树。
\(2.24.\) 考虑 \(n\) 个消息符号,假设它们出现的概率分别为 \(p_1,p_2,\cdots ,p_n\),任意 \(p_i\) 均是 \(\dfrac12\) 的幂且 \(\sum p_i =1\)。
\((1)\) 证明:概率最低的两个消息符号有相同的概率。
\((2)\) 证明:在此概率分布下,\(\text{Huffman}\) 编码的平均编码长度为 \(-\sum p_i \log p_i\).
解答
\((1)\) 考虑 \(\sum p_i =1\),记 \(p_i=\dfrac{1}{2^{k_i}}\),\(k_1 \ge k_2 \ge \cdots \ge k_n\),那么 \(2^{k_1} \sum p_i =\sum 2^{k_i-k_1}=2{k_1}\),那么也就是说 \(\sum 2^{k_i-k_1}\) 是偶数,而因为 \(2^{k_1-k_1}=1\),若 \(k_2>k_1\),则 \(\sum 2^{k_i-k_1}\) 是奇数,不成立。
故 \(k_1=k_2\),也就是 \(p_1=p_2\)。
\((2)\) 考虑算出 \(L(i)\)。
引理 \(L(i)=-\log p_i=k_i\)。
考虑归纳证明,\(n=1\) 时显然 \(L(i)=0\)。\(n>1\) 时,第一次合并 \(p_1,p_2\),得到 \(p'=p_1+p_2=2p_1\),还是 \(\dfrac12\) 的幂。显然 \(L(1)=L(2)=L'+1=-\log p'+1=-\log p_1\)。
故此时平均长度为 \(-\sum p_i \log p_i\)。
\(2.25.\) 证明:在 \(\nu\ge 3\) 阶的连通图 \(G\) 中,存在至少两个顶点,从 \(G\) 中删除这两个顶点后所得图仍然连通。
解答
构造一棵生成树 \(T\),删除两个树叶即可证明。
\(2.26.\) 为了在 \(4\) 枚硬币中找出一枚较轻的伪币,需要用天平称多少次?给出相应的算法。
\(2.27.\) 证明:非平凡树的最长轨道的起点和终点都是树叶。
解答
反证,若最长轨道 \(W\) 起点为 \(u\),终点为 \(v\),有一点不为树叶。
假设 \(u\) 不为树叶,则 \(\deg(u)>1\),考虑至少有一条边 \(e=uw\) 满足 \(e \notin W\)。若 \(w \in W\),那么出现圈,若 \(w \notin W\),那么 \(W+e\) 仍是一条轨道且更长,故无论如何都矛盾。
故 \(u,v\) 均是树叶。
图的连通性
顶连通度
定义 \(3.1\) 给定简单图 \(G=(V(G),E(G))\) 中一对不相邻的顶点 \(u,v\in V(G), u=v\)。若 \(S \subseteq V(G)-\{u,v\}\) 使得 \(u\) 与 \(v\) 在 \(G-S\) 中不连通,即分属两个不同的连通片,则称 \(S\) 是一个 \(uv\)-顶割集,简称为 \(uv\)-割集,也称 \(S\) 隔离了 \(u\) 与 \(v\)。含顶点最少的 \(uv\)-割集称为最小 \(uv\)-割集,其中的顶点数记为 \(c(u,v)\),称为 \(u\) 与 \(v\) 在 \(G\) 中的顶连通度,简称为 \(uv\)-连通度。若 \(u=v\) 或者 \(u\) 与 \(v\) 在 \(G\) 中相邻,则 \(uv\)-连通度没有定义。
定义 \(3.2\) 给定连通简单图 \(G=(V(G),E(G))\),以及 \(S \subset V(G)\),若 \(G-S\) 不连通,则称 \(S\) 是 \(G\) 的顶割集,简称割集。若一个割集中有 \(k\) 个元素,则称之为 \(k\)-顶割集。含顶点数最少的割集称为最小割集,其中的顶点数记为 \(\kappa(G)\),称为 \(G\) 的顶连通度,简称为连通度。
值得注意的是,完全图与非连通图都没有割集,不能应用上面的定义给出其连通度,但我们约定完全图的连通度为 \(\kappa(K_n) = n-1\),非连通图 \(G\) 的连通度为 \(\kappa(G) = 0\)。这种约定在讨论连通度的很多性质时,也符合一般图的连通度的定义。
对于非负整数 \(k\) 来说,若 \(\kappa(G) \ge k\),则称 \(G\) 是 \(k\)-连通的。当然,若 \(G\) 是 \(k\)-连通的,则也是 \((k-1)\)-连通的(\(k-1\ge 0\))。
而对于非完全图 \(G\) 来说,若 \(S\) 是 \(G\) 的顶割集,则 \(G-S\) 不连通,所以存在两个顶点 \(u,v\in V(G)-S\),使得 \(u\) 与 \(v\) 在 \(G-S\) 中没有轨道,由此可知,\(S\) 也是 \(uv\)-顶割集。也就是说,图 \(G\) 的任意一个顶割集,一定是某两个顶点之间的顶割集。反之,任意两个顶点之间的顶割集也一定是整个图的顶割集。所以,对于非连通图 \(G\),我们得到下面的结论:\(\kappa(G) = \min\{c(u,v)|u,v \in V(G),u \ne v,uv \notin E(G)\}\)。
假想图 \(G\) 表示一个通信网络,其中的顶点代表服务器或路由器,边代表通信链路。给定图 \(G\) 中的两个顶点 \(u,v\),以及 \(u\) 与 \(v\) 之间的两条轨道 \(P(u,v),Q(u,v)\)。若除了 \(u,v\) 之外,\(P(u,v)\) 与 \(Q(u,v)\) 还有其他的公共顶点 \(w\),则若顶点 \(w\) 出现故障的话,两条通信路径 \(P(u,v)\) 与 \(Q(u,v)\) 都不能使用。因此,从可靠性的角度,我们总是希望除了 \(u,v\) 之外,\(P(u,v)\) 与 \(Q(u,v)\) 没有其他的公共顶点,我们称这样的两条轨道为无公共内顶的 \(uv\)-轨道。记两两无公共内顶的 \(uv\)-轨道的最大数量为 \(p(u,v)\)。直观上来说,\(uv\)-连通度 \(c(u,v)\) 越大,应该 \(p(u,v)\) 越大。事实上,\(\text{Menger}\) 定理说明,若 \(u\) 与 \(v\) 在 \(G\) 中不相邻,两者就是相等的。
定义 设 \(G\) 是一个简单图,\(S \subset V(G)\),\(G\) 关于 \(S\) 的收缩图 \(G\cdot S\) 定义为:首先在 \(G\) 中删掉两个端点都在 \(S\) 中的边;再将 \(S\) 中所有的顶点收缩为一个顶点 \(s\);若 \(v \in V(G)-S\) 与 \(S\) 中某个顶点相邻,则在 \(G\cdot S\) 中将 \(v\) 与 \(s\) 连边;删掉重边与环。
定理 \(3.1(\text{Menger})\) 给定简单图 \(G\) 中两个不相邻的顶点 \(u,v\),\(G\) 中两两无公共内顶的 \(uv\)-轨道的最大数量等于最小 \(uv\)-割集中的顶点数,即:\(p(u,v) = c(u,v)\)。
证明
将 \(p,c,P\) 增添下标 \(p_G,c_G,P_G\) 表示 \(p,c,P\) 在图 \(G\) 下的定义,记 \(k=c_G(u,v)\),考虑对边数 \(\varepsilon\) 归纳。
显然由抽屉原理,若 \(p_G(u,v)>k\) 的话仅选择 \(|S|=k\) 的点集 \(S\) 不足以覆盖 \(p_G(u,v)\) 条两两无公共内顶的 \(uv\)-轨道,故显然 \(p_G(u,v) \le k\)。
只需证明 \(p_G(u,v) \ge k\),考虑找到 \(e=xy \in E\),\(e\) 与 \(u,v\) 均不关联,若无法找到 \(e\),则证明所有轨道 \(P_G(u,v)\) 长度均为 \(2\),容易证明,这里略去。
考虑 \(H=G-e\)。显然有 \(P_H\) 仍是 \(P_G\),且 \(H\) 中的割集 \(S\) 能直接获得一个 \(G\) 中的割集 \(S\cup \{x\}\),故 \(p_G(u,v) \ge p_H(u,v)=c_H(u,v) \ge c_G(u,v)-1 = k-1\)。
考虑反证,若 \(k > p_G(u,v) \ge k-1\),那么 \(p_G(u,v) = k-1\),且 \(p_G(u,v) = p_H(u,v)\),\(c_H(u,v) = c_G(u,v)-1\)。
考虑 \(H\) 中的一个割集 \(S=\{v_1,v_2,\cdots,v_k\}\),\(|S|=k-1\),故 \(S\) 不是 \(G\) 中的割集,也就是说 \(G-S\) 中还存在一条 \(uv\) 之间的轨道,那么这条轨道必须经过 \(e\)。
将 \(X\) 为所有 \(H-S\) 中 \(u\) 可达的点,\(Y\) 为其余的点(显然 \(v\) 可达),那么 \(x,y\) 一定分属于不同的点集,记 \(x\in X,y \in Y\)。
考虑 \(G_x=G\cdot X\),显然 \(G_x\) 中的割集一定是 \(G\) 中的割集,且 \(S \cup \{y\}\) 是 \(G_x\) 中的割集,再者,\(G_x\) 一定收缩了 \(ux\) 直接轨道的边,那么有 \(p_{G_x}(u,v)=c_{G_x}(u,v)=k\)。找到 \(G_x\) 中 \(k\) 条两两无公共内顶的 \(uv\)-轨道,这写轨道中一定包含 \(y,v_1,v_2,\cdots,v_{k-1}\) 到 \(v\) 之间 \(k\) 条两两无公共内顶的轨道,将 \(ab\) 之间的轨道记为 \(a \leadsto b\)。
\(G_y=G \cdot Y\) 同理,也就是说我们能构造出 \(u \leadsto x \rightarrow y \leadsto v\),\(u \leadsto v_1,v_2,\cdots,v_k \leadsto v\) 共 \(k\) 条两两无公共内顶的 \(uv\)-轨道,那么 \(p_G(u,v)=k-1\) 不成立,\(p_G(u,v)=k\)。
推论 \(3.1\) 给定简单图 \(G\),有 \(\min\{p(u,v)|u,v \in V (G),u \ne v,uv \notin E(G)\} = \min\{c(u,v)|u,v \in V (G),u \ne v,uv \notin E(G)\}\)。
定理 \(3.2(\text{Whitney})\) 任给简单图 \(G\),都有 \(\kappa(G) = \min\{p(u,v)|u,v ∈ V(G),u \ne v\}\)。
证明
\(G\) 为非连通图或完全图时容易证明,下面只证明 \(G\) 为非完全连通图。
我们发现该定理相比最小割集的结论只有 \(uv \in E\) 的部分不同。也就是说我们只需要证明对于任意 \(uv \in E\),存在 \(x\ne y,xy \notin E,p(x,y) \le p(u,v)\) 即可。
将 \(p,c,P\) 增添下标 \(p_G,c_G,P_G\) 表示 \(p,c,P\) 在图 \(G\) 下的定义。
考虑图 \(H=G-uv\),显然 \(p_G(u,v)=p_H(u,v)+1\),记 \(k=p_H(u,v)=c_H(u,v)\),考虑找到一个大小为 \(k\) 的 \(uv\)-顶割集 \(S\)。
若 \(V-S=\{u,v\}\),那么说明 \(\kappa(G) \ge p_G(u,v)=\nu-1\),是完全图,矛盾。
故存在 \(w \in V-S\),显然 \(w\) 在 \(H-S\) 中只能与 \(u\) 或 \(v\) 相邻,假设 \(w\) 与 \(v\) 相邻,显然 \(uw \notin E\)。
那么显然 \(S \cup \{v\}\) 是图 \(G\) 的一个 \(uw\) 顶割集,那么 \(p_G(u,w) \le k+1=p_G(v,w)\)。
这样我们将求连通度的算法由枚举一个子集的指数复杂度降低为可以用网络流求出最大轨道数量的多项式复杂度,在后续章节我们还会提到。
扇形定理
引理 \(3.1\) 假设简单图 \(G\) 是 \(k\)-连通图,在 \(G\) 中增加一个新的顶点 \(y\),并且在 \(G\) 中任意选取至少 \(k\) 个顶点,将 \(y\) 与这些选取的顶点各连一条边,得到的图记为 \(H\),则 \(H\) 也是 \(k\)-连通图。
证明
\(\nu(H) \ge k+1\),若 \(H\) 是完全图,则是 \(k\)-连通图。假设 \(|S|=k-1\) 且 \(S \subset V(H)\),只需证明 \(H-S\) 连通即可。
若 \(y \in S\),由于 \(H-S=G-(S- \{y\})\),而 \(G\) 是 \(k\)-连通图,故 \(G-(S- \{y\})\) 连通。
若 \(y \notin S\),由于 \(G\) 是 \(k\)-连通图,故 \(G-S\) 连通,且 \(y\) 在 \(H\) 中至少有 \(k\) 个邻顶,至少有一个 \(x \notin S,xy \in E(H)\)。
综上,\(H-S\) 连通。
推论 \(3.2\) 假设简单图 \(G\) 是 \(k\)-连通图,\(X,Y\) 是图 \(G\) 两个顶点子集,\(|X| \ge k\),\(|Y | \ge k\) 且 \(X \cap Y = \varnothing\),则 \(G\) 中存在 \(k\) 条无公共顶点的 \((X,Y)\)-轨道。其中 \((X,Y)\)-轨道指的是轨道的两个端点分属 \(X\) 与 \(Y\),而中间顶点不属于 \(X\cup Y\)。
证明
在 \(G\) 中增加两个顶点 \(x,y\),分别向 \(X,Y\) 中的每个顶点连边,得到图 \(H\)。由引理 \(3.1\),\(H\) 是 \(k\)-连通图。
找到 \(H\) 中的 \(k\) 条无公共内顶的 \(xy\)-轨道,删去这 \(k\) 条轨道上的顶点 \(x\) 与 \(y\),就得到 \(G\) 中的 \(k\) 条轨道 \(Q_1,Q_2,\cdots ,Q_k\),若 \(Q_i\) 中间有点 \(Q_{i,j} \in X\) 内,则删除 \(Q_{i,1} \sim Q_{i,j}\) 的一段,\(Q_{i,j} \in Y\) 同理,最终找到符合要求的 \(k\) 条轨道。
给定简单图 \(G\),\(x \in V(G), Y \subseteq V(G)-\{x\}\) 且 \(|Y| \ge k\),一组 \(k\) 条起点为
\(x\)、终点为 \(Y\) 中 \(k\) 个不同的顶点,且除了 \(x\) 之外无公共顶点的轨道称为从 \(x\) 到 \(Y\) 的 \(k\)-扇形。
推论 \(3.3(\text{扇形定理})\) 假设简单图 \(G\) 是 \(k\)-连通图,\(x\in V(G),Y \subseteq V(G)-\{x\}\) 且 \(|Y| \ge k\),则 \(G\) 中存在从 \(x\) 到 \(Y\) 的 \(k\)-扇形。
定理 \(3.3(\text{Dirac})\) 设 \(S\) 是 \(k\)-连通图 \(G\) 中的 \(k\) 元顶点子集,\(k \ge 2\),则 \(G\) 中存在一个圈 \(C\),使得 \(S\) 中所有的顶点都在 \(C\) 上。
证明思路是对 \(k\) 归纳,过于复杂故这里略去,感兴趣的读者可以自行证明。
边连通度
定义 \(3.3\) 给定简单图 \(G=(V(G),E(G))\) 的一对顶点 \(u,v, u\ne v\)。若边子集 \(E' \subseteq E(G)\) 使得 \(u\) 与 \(v\) 在 \(G-E'\) 中不连通,即分属两个不同的连通片,则称 \(E'\) 是一个 \(uv\)-边割集。含边数最少的 \(uv\)-边割集称为最小 \(uv\)-边割集,其中的边数记为 \(c'(u,v)\),称为 \(u\) 与 \(v\) 在 \(G\) 中的边连通度,简称为 \(uv\)-边连通度。
定义 \(3.4\) 给定连通简单图 \(G=(V(G),E(G))\),以及 \(E'\subseteq E(G)\),若 \(G-E'\) 不连通,则称 \(E'\) 是 \(G\) 的边割集。若一个边割集中有 \(k\) 条边,则称之为 \(k\)-边割集。含边数最少的边割集称为最小边割集,其中的边数记为 \(\kappa'(G)\),称为 \(G\) 的边连通度。若图 \(G\) 不是连通图,就定义 \(\kappa'(G)=0\)。
若 \(\kappa'(G) \ge k\),则称图 \(G\) 是 \(k\)-边连通的。对于 \(k>0\) 来说,若 \(G\) 是 \(k\)-边连通的,则也是 \((k-1)\)-边连通的。
给定图 \(G\) 的两个不同的顶点 \(u,v \in V(G)\),我们称 \(u\) 与 \(v\) 之间两两无公共边的最大轨道数为无公共边的轨道的最大数量,记为 \(p'(u,v)\)。
定理 \(3.4(\text{Menger})\) 给定图 \(G\) 中两个顶点 \(u,v\),\(G\) 中两两无公共边的 \(uv\)-轨道的最大数量等于最小 \(uv\)-边割集中的边数,即 \(p'(u, v) = c'(u,v)\)。
只需要使用边图即可用 \(\text{Menger}\) 定理点版本证明边版本,读者自证不难。
我们可以得出 \(\kappa'(G) = \min\{p'(u,v)|u,v \in V(G),u \ne v\}\)。
定理 \(3.5\) 假定 \(G\) 是简单图,则有 \(\kappa(G) \le \kappa'(G) \le \delta(G)\)。
根据原始定义证明不难,这里省略。
割顶、桥与块
定义 \(3.5\) 给定连通简单图 \(G=(V(G),E(G))\),若存在顶点 \(v\),使得 \(G-v\) 不连通,即 \(\{v\}\) 是割集,则称 \(v\) 是 \(G\) 的割顶。
若连通图 \(G\) 有割顶 \(v\),则 \(\kappa(G)=1\),而 \(v\) 则是 \(G\) 的关键顶点,在网络设计中就是重要的节点,需要重点保护。下面的定理给出了割顶的特性。
定理 \(3.6\) 设 \(G\) 是连通图,\(v \in V(G)\),则下述命题等价:
\((1)\) \(v\) 是 \(G\) 的割顶。
\((2)\) 存在与 \(v\) 不同的两个顶点 \(u,w\in V(G)-\{v\}\),使得 \(v\) 在每一条从 \(u\) 到 \(w\) 的轨道上。
\((3)\) 存在 \(V(G)-\{v\}\) 的一个划分 \(V(G)-\{v\}=U \cup W,U \cap W = \varnothing,U \ne \varnothing, W \ne \varnothing\),使得任给 \(u \in U,w \in W\),\(v\) 在每一条从 \(u\) 到 \(w\) 的轨道上。
证明
\((1) \Rightarrow (3)\):考虑 \(U,W\) 在 \(G-v\) 中不同的连通片,那么显然 \(u,w\) 在 \(G-v\) 中不连通,\(G\) 中连通,那么每条 \(u,w\) 之间的轨道都经过 \(v\)。
\((3) \Rightarrow (2)\):显然是特例。
\((2) \Rightarrow (1)\):考虑删除 \(v\) 后 \(u,w\) 不连通,则 \(v\) 是割顶。
定义 \(3.6\) 给定连通简单图 \(G=(V(G),E(G))\),若存在边 \(e\),使得 \(G-e\) 不连通,也就是 \(\{e\}\) 是边割集,则称 \(e\) 是 \(G\) 的桥(或割边)。
若连通图 \(G\) 有桥 \(e\),则 \(\kappa'(G)=1\),定理 \(3.6\) 刻画的是连通性中关键顶点的特征,而下面的定理刻画的则是连通性中关键边的特征。
定理 \(3.7\) 设 \(G\) 是连通图,\(e \in E(G)\),则下述命题等价:
\((1)\) \(e\) 是 \(G\) 的桥。
\((2)\) \(e\) 不在 \(G\) 的任一圈上。
\((3)\) 存在 \(u,w \in V(G)\),使得 \(e\) 在每一条从 \(u\) 到 \(w\) 的轨道上。
\((4)\) 存在 \(V(G)\) 的一个划分 \(V(G)=U \cup W,U \cap W = \varnothing,U \ne \varnothing,W \ne \varnothing\),使得任给 \(u \in U,w \in W\),\(e\) 在每一条从 \(u\) 到 \(w\) 的轨道上。
定义 \(3.7\) 没有割顶的简单图 \(G\) 称为块。若 \(G\) 不是块,则 \(G\) 的成块的极大子图称为 \(G\) 的块。
按照定义 \(3.7\),若 \(G\) 是一个顶点的平凡图或 \(G=K_2\),则 \(G\) 是块,这两种情况都是平凡情况,其连通度分别为 \(0\) 与 \(1\)。在 \(\nu(G) \ge 3\) 时,则若 \(G\) 是块,一定有 \(\kappa(G) \ge 2\)。
定理 \(3.8\) 设 \(G\) 是连通图,\(\nu(G) \ge 3\),则下述命题等价:
\((1)\) \(G\) 是块。
\((2)\) 任给 \(u,v \in V(G),u \ne v\),\(u\) 与 \(v\) 在 \(G\) 的同一个圈上。
\((3)\) 任给 \(u \in V(G),e \in E(G)\),\(u\) 与 \(e\) 在 \(G\) 的同一个圈上。
\((4)\) 任给 \(e_1,e_2 \in E(G)\),\(e_1\) 与 \(e_2\) 在 \(G\) 的同一个圈上。
\((5)\) 任给 \(u,v \in V(G),u \ne v, e \in E(G)\),存在连接 \(u\) 与 \(v\) 的轨道 \(P(u,v)\),使得 \(e\) 在 \(P(u,v)\) 上,即 \(e \in E(P(u,v))\)。
\((6)\) 任给三个不同的顶点 \(u,v,w\in V(G)\),存在连接 \(u\) 与 \(v\) 的轨道 \(P(u,v)\),使得 \(w\) 在轨道 \(P(u,v)\) 上。
\((7)\) 任给三个不同的顶点 \(u,v,w \in V(G)\),存在连接 \(u\) 与 \(v\) 的轨道 \(P(u,v)\),使得 \(w\) 不在轨道 \(P(u,v)\) 上。
证明留给感兴趣的读者思考。
可靠通信网的构造
对于任意图或带权图来说,最小 \(k\)-连通子图是难以求解的。
我们考虑完全图 \(K_n\),若其每条边的权值都是 \(1\),则其权最小的 \(k\)-连通生成子图就是构造一个 \(n\) 个顶点且边数最少的 \(k\)-连通图。
假设 \(n\) 个顶点的 \(k\)-连通图至少需要 \(f(n,k)\) 条边,设该图为 \(G_{\min}\)。由连通度的定义知,合理的假设是 \(k<n\)。
显然 \(f(n,k)=\dfrac{1}{2} \sum\limits_{v \in V} \deg(v) \ge \left\lceil \dfrac{n \delta}{2} \right\rceil \ge \left\lceil \dfrac{nk}{2} \right\rceil\)。
下面会构造一个 \(\varepsilon=f(n,k)\) 的图 \(H_{n,k}\),令 \(V=\{0,1, \cdots,n-1\}\)。
\((1)\) \(k\) 是偶数。记 \(k =2r\)。\(H_{n,2r}\) 的构造方法为:两个不同的顶点 \(i\) 与 \(j\) 相邻当且仅当 \(i-r \le j \le i+r\),其中的加法是在 \(\bmod\,n\) 的意义下进行的。
\((2)\) \(k\) 是奇数,\(n\) 是偶数。记 \(k=2r+1\)。\(H_{n,2r+1}\) 的构造方法是:先构造 \(H_{n,2r}\),然后在 \(H_{n,2r}\) 的基础上,将顶点 \(i\) 与顶点 \(i+\dfrac{n}2 \left(0 \le i \le \dfrac{n}2 -1\right)\) 连边。
\((3)\) \(k\) 是奇数,\(n\) 是奇数。记 \(k=2r+1\)。\(H_{n,2r+1}\) 的构造方法是:先构造 \(H_{n,2r}\),然后在 \(H_{n,2r}\) 的基础上,将顶点 \(0\) 与顶点 \(\dfrac{n-1}2,\dfrac{n+1}2\) 各连一条边,再将顶点 \(i\) 与顶点 \(i+\dfrac{n+1}2 \left(1 \le i \le \dfrac{n-3}2\right)\) 连边。
定理 \(3.9(\text{Harary}, 1962)\) \(H_{n,k}\) 是 \(k\)-连通图。
证明
以下证明均在 \(\bmod\,n\) 意义下进行。
考虑先证明 \(k=2r\) 的情况。反证,若存在 \(V' \subseteq V\) 且 \(|V'| <2r\) 使得 \(i<j\) 在 \(G-V'\) 中不连通。
找到 \(G\) 中两条轨道 \(W_1=(i,i+1,\cdots,j-1,j)\) 和 \(W_2=(j,j+1,\cdot,n-1,0,\cdots, i-1,i)\),必有其中一条轨道 \(W\) 满足 \(|W \cap V'|<r\)。考虑 \(W=(v_1,v_2,\cdots,v_p)\),那么必有 \(v_{i+1} \le v_i+r\),那么 \(v_i,v_{i+1}\) 之间有边,\(W-V'\) 仍是一条轨道,那么 \(i,j\) 仍连通,矛盾。
故 \(k=2r\) 时 \(H_{n,k}\) 是 \(k\)-连通图。
考虑 \(k=2r+1\),仿照上述证明,若存在 \(|W \cap V'|<r\) 则矛盾。否则 \(|W_1 \cap V'|=|W_2 \cap V'|=r\) 且必须删去的是连续的长度为 \(r\) 的两条轨道。
记 \(i,j\) 所在的连通片分别为 \(S,T\),它们在 \(G\) 上是编号连续的一条轨道。考虑分别从 \(S,T\) 中选择一个轨道端点 \(s,t\) 满足 \(t=s+r+1\)。
若 \(n\) 为偶数,那么与 \(s,t\) 有额外连边的点是 \(s'=s+\dfrac12,t'=t+\dfrac{1}{2}\),显然它们都被删除,而又恰好在被删除的另一条轨道上,但它们之间的距离为 \(t'-s'=r+1\),也就是说这条轨道长度为 \(r+2\),矛盾。
若 \(n\) 为奇数,证明几乎相同,对于与 \(0\) 有额外连边的点随便选一条即可。
故 \(k=2r+1\) 时 \(H_{n,k}\) 是 \(k\)-连通图。
故 \(H_{n,k}\) 是 \(k\)-连通图。
这里我们发现 \(H_{n,k}\) 也是 \(k\)-边连通图,记 \(g(n,k)\) 为 \(n\) 个顶点的 \(k\)-边连通图所需的最少边数,有 \(f(n,k)=g(n,k)=\left\lceil \dfrac{nk}{2} \right\rceil\)。
习题
\(3.1.\) \(G\) 是 \(k\)-边连通图,\(E'\) 是 \(G\) 的 \(k\) 条边的集合,则 \(\omega(G-E') \le 2\)。
解答
反证,若 \(\omega(G-E') > 2\),考虑任取 \(uv \in E'\),若 \(uv\) 在 \(G-E'\) 中分属于不同连通片,那么 \(\omega(G-(E'-uv))=\omega(G-E')-1>1\),否则 \(\omega(G-(E'-uv))=\omega(G-E')>2\),\(E'-uv\) 是一个边数更少的边割集,\(\kappa' <k\),矛盾。
\(3.2.\) 给出一个 \(k\)-连通图 \(G\) 以及 \(k\) 个顶点的集合 \(V'\),使得 \(\omega(G-V')>2\)。
\(3.3.\) \(G\) 是简单图,\(\delta(G) \ge \nu(G)-2\),则有 \(\kappa(G)=\delta(G)\)。
解答
若 \(\delta = \nu -1\),那么显然 \(\kappa=\delta=\nu-1\)。
若 \(\delta = \nu -2\),那么考虑对所有 \(uv \notin E\),任取 \(w \in V- \{u,v\}\),\(uw,wv \in E\),故 \(p(u,v)=\nu-2\),那么显然 \(\kappa=\delta=\nu-2\)。
\(3.4.\) 给出一个简单图 \(G\),满足 \(\delta(G)=\nu(G)-3\) 且 \(\kappa(G)<\delta(G)\)。
\(3.5.\) \(G\) 是简单图,\(\delta(G) \ge \dfrac{\nu(G)}2\),则有 \(\kappa'(G)=\delta(G)\)。
解答
首先 \(\kappa'\le \delta\)。
然后考虑最小边割集 \(E'\) 将 \(G\) 分成 \(G[V']\) 和 \(G[V-V']\) 两个部分。
显然在 \(|E'|\) 是 \(uv\in E,u\in V',v \notin V'\) 的边的数量。
令 \(|V'| \le |V-V'|\),记 \(\nu'=|V'|\),显然 \(|E'| \ge \delta\nu' - \dfrac{\nu'(\nu'-1)}{2}=(\delta-\dfrac{\nu'}{2}+\dfrac{1}{2})\nu'\),在 \(\nu'=1\) 时取到最小值 \(\delta\),那么 \(\kappa'=\delta\)。
\(3.6.\) \(G\) 是简单图,\(\delta(G) \ge \dfrac12 (\nu(G)+k-2)\),则 \(G\) 是 \(k\)-连通图。
解答
考虑反证,若存在 \(V' \subseteq V,|V'| \le k-1\),使得 \(G-V'\) 不连通。
考虑 \(G'=G-V'\),那么 \(\delta'\ge\delta-k+1\ge \dfrac12(\nu-k) \ge \dfrac12(\nu'+1)\)。也就是说对于 \(G-V'\) 中若存在 \(G_1,G_2\) 不连通,考虑两者点集较小的(设是 \(G_1\))大小为 \(p\),有 \(p \le \dfrac{\nu'}{2}\),也就是说 \(\dfrac{p(p-1)}{2} < \delta p\),故 \(G_1,G_2\) 之间存在边,矛盾。
\(3.7.\) 任给三个非负整数 \(l,m,n\),都存在简单图 \(G\),满足 \(\kappa(G)=l,\kappa'(G)=m,\delta(G)=n\)。
解答
考虑两个完全图 \(K_n\) 之间一侧的 \(l\) 个点想另一次 \(m\) 个点共连 \(l\) 条边,满足要求。
\(3.8.\) 设 \(P(u,v)\) 是 \(2\)-连通图 \(G\) 中的一条轨道,\(G\) 中是否一定存在另一条轨道 \(Q(u,v)\),使得 \(P(u,v)\) 与 \(Q(u,v)\) 没有公共内顶?
\(3.9.\) 证明:若简单图 \(G\) 不含偶圈与孤立顶点,则 \(G\) 的块是 \(K_2\) 或奇圈。
解答
令 \(G\) 是块,对所证命题无影响。
若 \(\nu=2\),那么 \(G=K_2\),成立。
若 \(\nu>2\),考虑反证。
若 \(G\) 不存在圈,那么 \(G\) 是树,存在割顶,矛盾。
若 \(G\) 中存在偶圈,矛盾。
\(G\) 中存在至少一个奇圈 \(W_c\)。若有点 \(v\) 或有边 \(e\) 不在圈上,那么由于 \(G\) 是块,那么也存在一条轨道 \(W\) 使得 \(v\) 或者 \(e\) 在 \(W\) 上且仅有 \(W\) 的两个端点在 \(W_c\) 上,且 \(W\) 与 \(W_c\) 无公共边。
考虑 \(W\) 的两个端点 \(u,w\) 将圈分为 \(W_1\) 和 \(W_2\) 两条轨道,由于 \(W_c\) 长度是奇数,也就是 \(W_1,W_2\) 长度奇偶性不同,也就是说圈 \(W+W_1\) 和圈 \(W+W_2\) 至少有一个长度为偶数,矛盾。
\(3.10.\) 设子图 \(G_1\) 与 \(G_2\) 是图 \(G\) 的两个不同的块,则若 \(G_1\) 与 \(G_2\) 有公共顶点 \(v\),则 \(v\) 一定是 \(G\) 的割顶。
解答
考虑反证,若 \(v\) 不是割顶,则 \(G_1,G_2\) 不是极大的成块子图。
由于 \(v\) 不是割顶,那么 \(G-v\) 连通,考虑任取 \(x \in V(G_1)-v,y \in V(G_2)-v\),找到 \(x,y\) 在 \(G-v\) 中的任意一条轨道 \(W\)。
引理 \(G'=G_1 \cup G_2 \cup W\) 是一个成块子图。
显然 \(G'-v\) 连通,若删除 \(u \in G_1\),那么 \(G_1\) 连通,\(G_1-u\) 与 \(G_2\) 有公共点,\(W\) 与 \(G_2\) 有公共点,那么 \(G'-u\) 连通,\(u \in G_2\)、\(u \in W\) 同理。
那么我们找到一个更大的成块子图,矛盾。
\(3.11.\) 设 \(G\) 是连通图,且不是块,则在 \(G\) 中至少存在两个块,每个块仅含 \(G\) 的一个割顶。
解答
显然每个点至少存在于一个块,且 \(G\) 不是块,那么至少两个块。
反证,考虑若块 \(G'\) 内不存在割顶,那么至少存在 \(uv \in E,u \in V(G'),v \notin V(G')\)。
\(G-u\) 连通,找到 \(v,w(w \in V(G'))\) 之间的轨道 \(W\),之后类似于 \(3.10.\) 的证明,\(G'\cup W\) 是一个更大的成块子图,矛盾,每个块内至少有一个割顶。
\(3.12.\) 设 \(G\) 是简单图。若任给 \(e\in E(G)\),都有 \(\kappa (G-e)<\kappa (G)\),则称 \(G\) 是 \(\kappa\) 临界图。证明:
\((1)\) 每个 \(\kappa\) 临界 \(2\)-连通图都有一个度数为 \(2\) 的顶点。
\((2)\) 若 \(G\) 是 \(κ\) 临界 \(2\)-连通图,且 \(\nu(G) \ge 4\),则 \(\varepsilon(G) \le 2\nu(G)-4\)。
\((3)\) 任给 \(n\ge 4\),请给出 \(n\) 个顶点,\(2n-4\) 条边的最小 \(2\)-连通图,参见本章习题 \(25\) 中的定义。
解答
\((1)\) 考虑反证。考虑 \(e=uv \in E\),\(\kappa(G)-1 \le \kappa(G-e)<\kappa(G)=2\),故 \(\kappa(G-e)=1\),存在割顶 \(w\)。
若 \(u,v\) 在 \(G-e-w\) 中连通,那么 \(G-w\) 连通性与 \(G-e-w\) 连通性相同,\(w\) 是 \(G\) 中割顶,矛盾。也就是 \(u,v\) 在 \(G-e-w\) 中不连通。
那么 \(p_G(u,v)=2\),考虑在 \(G-e\) 中找到一条以 \(v\) 为起点的最长轨道 \(W\),满足 \(u \in W\),记另一个端点为 \(x\)。由于 \(\deg(x) \ge 3\),所以 \(xy,xz \notin W\) 一定存在,因为 \(W\) 最长,所以 \(y,z \in W-x\),假设在 \(W\) 上 \(x,y\) 之间距离比 \(x,z\) 近,那么 \(p(x,y)=3\),矛盾。
故 \(\delta =2\)。
\((2)\) 考虑一个较弱的条件:找到一棵生成树 \(T\),只需任给 \(e \notin E(T)\) 时有 \(\kappa (G-e)<\kappa (G)\)。
对于 \(e=uv \notin E(T)\),考虑删除 \(e\) 后只有 \(u,v\) 轨道上的点才有可能成为割顶(\(u,v\) 除外)。
也就是说,可以视为先删除某个 \(u,v\) 轨道上的点后,\(e\) 成为了割边。对于每个点 \(x\) 来说,只能新增 \(\deg(x) -1\) 条割边。有 \(\varepsilon \le \nu - 1+ \sum (\deg(v)-1) =2\nu -3\)。
不难讨论得到当 \(\nu \ge 4\),\(\varepsilon =2\nu -3\) 时总有树边不合法,那么 \(\varepsilon \le 2\nu-4\)。
\((3)\) 一个长度为 \(4\) 的圈符合条件。
\(3.13.\) 证明定理 \(3.4\)。
解答
考虑构造出边图,直接归纳为点版本,得证。
\(3.14.\) 证明定理 \(3.7\)。
解答
\((1) \Rightarrow (2)\) 反证,若 \(e\) 在圈上,则 \(G-e\) 和 \(G\) 连通性相同,矛盾。
\((2) \Rightarrow (3)\) 反证,若对于所有 \(u,v\),都有至少一条不过 \(e\) 的轨道 \(W_{u,v}\),那么记 \(e=xy\),那么 \(e\) 和 \(W_{x,y}\) 构成一个圈,矛盾。
\((3) \Rightarrow (4)\) \(U\) 为所有在 \(G-e\) 中与 \(x\) 连通的点,\(W\) 为所有在 \(G-e\) 中与 \(y\) 连通的点,显然 \(U \cup W = V\),若 \(U \cap W \ne \varnothing\),根据连通性有 \(U=W\),那么 \(x,y\) 有不经过 \(e\) 的轨道。显然 \(u\in U,v\in W\),\(u,v\) 在 \(G-e\) 不连通,在 \(G\) 中轨道一定经过 \(e\)。
\((4) \Rightarrow (1)\) 显然任取 \(x \in U,y \in W\),\(x,y\) 在 \(G-e\) 中不连通,\(e\) 是桥。
\(3.15.\) 证明:只有两个顶点不是割顶的连通图是一条轨道。
解答
\(\nu=2\) 时显然,接下来令 \(\nu \ge 3\)。
找到 \(G\) 中的一棵生成树 \(T\)。\(T\) 中至少两个树叶。
引理 \(T\) 中的树叶在 \(G\) 中一定不是割顶。
考虑树叶 \(v\),\(T-v\) 连通,故 \(G-v\) 连通。
\(T\) 至少两个树叶,也就是说分支点都是割顶且 \(T\) 是一条轨道。若存在 \(uv \notin E(T)\),那么 \(u,v\) 在树上的轨道上的点(除了 \(u,v\))都一定不是割顶(在环上),也就是说 \(G=T\),是一条轨道。
\(3.16.\) 若图 \(G\) 的每个顶点的度数都是偶数,则 \(G\) 中没有桥。
解答
反证,假设 \(e=xy\) 是割边,考虑 \(G-e\) 被分为两个连通片 \(x \in G_1,y \in G_2\)。显然 \(\sum\limits_{v \in V(G_1)} \deg(v) \equiv 2\varepsilon \equiv 0 \pmod2\),但是 \(\sum\limits_{v \in V(G_1) - x} \deg(v)+\deg(x) \equiv 1 \pmod 2\),矛盾。
\(3.17.\) \(G\) 是连通图,且 \(\nu(G) \ge 3\)。证明:
\((1)\) 若 \(G\) 有桥,则存在 \(v\in V(G)\),使得 \(\omega(G-v)>\omega(G)\)。
\((2)\) 结论 \((1)\) 的逆未必成立。
解答
\((1)\) 删除割边相关的某个顶点即可。
\((2)\) 构造一张有割顶无割边的图即可。
\(3.18.\) \(3\)-正则图有割顶当且仅当有桥。
解答
\(\nu \ge 4\),显然有割边必有割顶。
假设 \(v\) 是割顶,考虑 \(G-v\),那么由于三次正则图,所以最多分为三个连通片。
若 \(\omega(G-v)=3\),那么显然 \(vu_i \in E\) 的 \(u_i\) 在不同的 \(G_i\) 中,三条边均是割边。
若 \(\omega(G-v)=2\),那么由抽屉原理,\(vu_i \in E\) 中有两个 \(u_i\) 在同一个 \(G_i\),剩下那条边是割边。
\(3.19.\) 给定 \(n\) 维超立方体 \(H_n\) 中的两个顶点 \(u=(0,0,\cdots ,0)\) 和 \(v=(1,1,\cdots ,1)\)。请给出 \(H_n\) 中最大的无公共边的 \(uv\)-轨道的集合和最小的 \(uv\)-顶割集。
\(3.20.\) 设 \(e\) 是 \(2\)-连通图 \(G\) 的一条边,若将边收缩后,得到的图 \(G\cdot e\) 也是 \(2\)-连通图,则称 \(e\) 是可收缩的。证明:每个 \(\nu(G) \ge 3\) 的 \(2\)-连通图 \(G\) 都有一条可收缩边。
解答
考虑若 \(e=uv\) 不可收缩,那么 \(G \cdot e\) 中有割顶,显然新割顶是 \(u,v\) 合并成的新点,否则连通性没有改变。
考虑 \(G\) 的一棵生成树 \(T\),任取根定向,找到 \(e=uv \in E(T)\) 且 \(v\) 是深度最深的树叶的边。显然此时 \(u\) 的所有儿子均为树叶。
考虑任取 \(u\) 的其他儿子 \(w\),若有 \(xw \in E(T)\) 满足 \(x \ne u,x \ne v\),那么删去 \(uw\),连接 \(wx\)。
若操作完后 \(u\) 只有 \(v\) 一个儿子,那么 \(T \cdot e\) 中 \(\{u,v\}\) 显然不是割顶,\(e\) 可收缩。
否则存在某个树叶满足 \(vw \in E(T)\),此时明显 \(vw\) 可收缩。
\(3.21.\) 设 \(e\) 是 \(2\)-连通图 \(G\) 的一条边,若将边删除后,得到的图 \(G-e\) 也是 \(2\)-连通图,则称 \(e\) 是可删除的。证明:\(\nu(G) \ge 4\) 的 \(2\)-连通图 \(G\) 每一条边要么是可收缩的,要么是可删除的。
解答
若 \(e=uv\) 不可删除,则 \(G-e\) 中存在割顶,找到一个记为 \(w\),显然 \(w \ne u\) 且 \(w \ne v\)。
考虑 \(G-w\) 连通,故 \(G-w-e\) 最多两个连通片 \(u \in G_1,v \in G_2\)。考虑 \(x \in G_1\) 与 \(v\) 之间不经过 \(u\) 的轨道 \(W\),若 \(w \notin W\),那么与 \(G-w-e\) 不连通矛盾。否则 \(x,w\) 在 \(G-u-v\) 中连通,\(G_2\) 同理,所以 \(e\) 可收缩。
\(3.22.\) 证明扇形定理(推论 \(3.3\))。
解答
考虑新建节点 \(z\) 并与所有 \(y \in Y\) 连边,由引理 \(3.1\),\(G'\) 也是 \(k\)-连通图,那么 \(x,z\) 之间存在 \(k\) 条中间点不交的轨道,经过简单处理后得到一个 \(k\)-扇形。
\(3.23.\) 构造一个 \(5\)-连通图 \(G\) 以及 \(G\) 中的 \(4\) 个顶点 \(x_1,y_1,x_2,y_2\),满足 \(G\) 中没有圈能够使得这四个顶点按照给定的顺序在圈上出现。注:对于 \(6\)-连通图来说,四个顶点则可以按照任意给定的顺序在圈上出现。
解答
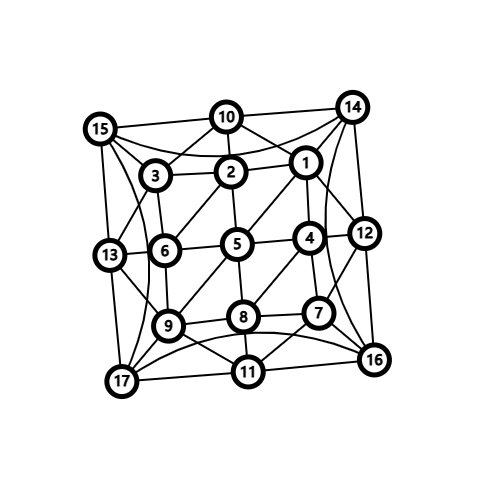
不难发现不存在一个圈使得圈上顶点按 \(14,15,16,17\) 的顺序出现。
\(3.24.\) 设 \(G\) 是一个图,\(x \in V(G),Y \subseteq V(G)-\{x\}\),\(Z \subseteq V(G)-\{x\}\),\(|Y|<|Z|\)。假设从 \(x\) 到 \(Y\) 与从 \(x\) 到 \(Z\) 都存在扇形,则存在 \(z \in Z-Y\),使得从 \(x\) 到 \(Y \cup \{z\}\) 存在扇形。
解答
找到 \(x\) 到 \(Y,Z\) 的扇形,考虑 \(Z\) 扇形中每条轨道与 \(Y\) 扇形中轨道的交。若 \(z_i\) 与 \(Y\) 扇形无交,则找到 \(x\) 到 \(Y \cup \{z_i\}\) 的扇形。
记 \(p_i\) 表示轨道 \(z_i\) 与 \(Y\) 扇形的距离 \(x\) 最近的交是在 \(y_{p_i}\) 轨道上。由抽屉原理,存在 \(p_i=p_j\),考虑交点离 \(y_i\) 最近的轨道,假设交点在 \(k_i\),将 \(Y\) 扇形中 \(x\) 到 \(k_i\) 的部分替换为 \(Z\) 扇形中 \(x\) 到 \(k_i\) 的部分。
显然 \(Y\) 仍是扇形,并且至少消去了一个 \(Y\) 扇形与 \(Z\) 扇形中的交点,所以最后调整总会结束到一个存在轨道 \(z_i\) 与 \(Y\) 扇形无交的情况,找到 \(Y \cup \{z_i\}\)。
\(3.25.\) 设 \(G\) 是 \(k\)-边连通图,若任给 \(e\in E(G)\),\(G-e\) 都不是 \(k\)-边连通图,则称 \(G\) 是最小 \(k\)-边连通图。
\((1)\) 若 \(G\) 是最小 \(k\)-边连通图,证明:
\((a)\) 任给 \(e\in E(G)\),\(e\) 都在 \(G\) 的某个 \(k\)-边割集中。
\((b)\) \(G\) 中有一个度数为 \(k\) 的顶点。
\((c)\) \(\varepsilon(G) \le k(\nu(G)-1)\)。
\((2)\) 证明:任意 \(k\)-边连通图 \(G\) 都存在一个边数最多为 \(k(\nu(G)-1)\) 的 \(k\)-边连通生成子图。
解答
\((1)\) \((a)\) \(G-e\) 的最小边割集 \(S\) 大小为 \(k-1\),那么 \(S \cup \{e\}\) 是 \(G\) 的大小为 \(k\) 的边割集,是 \(k\)-边割集。
\((b)\) 反证,假设 \(\delta > k\),考虑一个 \(|S|\) 最小的、\(|(S,\bar{S})|=k\) 的割。若 \(|S|=1\) 则矛盾。考虑 \(|S|>1\),若不存在 \(xy\in E\),\(x,y \in S\),那么 \(S\) 显然可以更小,矛盾,否则任取 \(xy\),可以找到 \(|(T,\bar{T})|\) 将 \(x,y\) 分隔,此时 \(|(S\cap T,\overline{S\cap T})|=k\),显然 \(|S \cap T|<|S|\),矛盾,故 \(\delta=k\)。
\((c)\) 找到一个至多 \(k\) 条边的割 \((S,\bar{S})\),然后递归割开 \(S,\bar{S}\) 即可,最多割 \(\nu-1\) 次所有集合大小均为 \(1\),故 \(\varepsilon \le k(\nu-1)\)。
\((2)\) 考察 \(G-e\) 是否是 \(k\)-边连通图,若是则删除 \(e\) 即可,最终会得到一个最小 \(k\)-边连通图。
\(3.26.\) 画出 \(H_{8,3}\) 和 \(H_{9,3}\)。
\(3.27.\) 证明:当 \(k\) 为奇数时,\(H_{n,k}\) 是 \(k\)-连通图。
\(3.28.\) 设 \(G\) 是满足 \(\nu(G) \ge 3\) 的 \(k\)-边连通图,则任给 \(e\in E(G)\),\(G \cdot e\) 仍是 \(k\)-边连通图。
解答
显然 \(G \cdot e\) 中的边割集仍是 \(G\) 中的边割集,\(k' \ge k\),证毕。
平面图
平面图及平面嵌入
定义 \(4.1\) 如果一个图可以画在平面上,使得除了端点外,它的任意两条边没有交点,则称这个图为可嵌入平面的,简称平面图。平面图 \(G\) 的这样一种画法(图示)称为 \(G\) 的一个平面嵌入。
图 \(G\) 的一个平面嵌入 \(G'\) 本身可看作与 \(G\) 同构的图,因此有时把平面图的平面嵌入称为平图。
平面嵌入的概念也可以推广到其他曲面上去。若图 \(G\) 能画在曲面 \(S\) 上使它的边仅在端点相交,则图 \(G\) 称为可嵌入曲面 \(S\) 的;图 \(G\) 的这样一种画法(如果存在)称为 \(G\) 的一个 \(S\) 嵌入。其中与平面嵌入密切相关的是球面嵌入。
定理 \(4.1\) 图 \(G\) 可嵌入平面,当且仅当 \(G\) 可嵌入球面。
当把平面图 \(G\) 平面嵌入以后,为方便起见,把此时 \(G\) 的图示仍记为 \(G\)。平图 \(G\) 把平面划分为若干连通的闭区域,这些闭区域称为 \(G\) 的面。
每个平图恰有一个无界的面,称为外部面。
定理 \(4.2\) 设 \(v\) 是平面图 \(G\) 的顶点,则存在 \(G\) 的一个平面嵌入,使得 \(v\) 在这个嵌入的外部面上。
我们用 \(b(f)\) 表示平图 \(G\) 中面 \(f\) 的边界。若 \(G\) 是连通的,则 \(b(f)\) 可以认为是一条回路,若面 \(f\) 中含有桥,则每条桥都被这条回路经过两次;当面 \(f\) 中不包含桥时,这条回路是 \(G\) 的一个圈。
定义 \(4.2\) 称面 \(f\) 与它的边界上的顶点和边是关联的。若 \(e\) 是平图的桥,则只有一个面和 \(e\) 关联;否则有两个面和 \(e\) 关联。称一条边分隔和它关联的面. 面 \(f\) 的度数 \(\deg(f)\) 是和它关联的边数,即 \(b(f)\) 中的边数,其中桥被计算两次。
定理 \(4.3\) 任给平面图 \(G\),\(\sum\limits_{f \in F(G)} \deg(f) = 2|E(G)|\),其中 \(F(G)\) 表示 \(G\) 中所有面构成的集合。
\(\text{Euler}\) 对连通平图中顶点、边和面的数目建立了一个简单的公式,称为 \(\text{Euler}\) 公式。
定理 \(4.4\) 设 \(G\) 是连通平图,有 \(\nu\) 个顶点,\(\varepsilon\) 条边,\(\phi\) 个面,则 \(\nu-\varepsilon+\phi=2\)。
证明
对 \(\phi\) 归纳,若 \(\phi=1\) 则 \(G\) 是树,成立。
若 \(\phi>1\),找到一个圈 \(C\),删除一种一条边 \(e\),\(G-e\) 连通,且 \(\varepsilon,\phi\) 各减一,等式仍成立。
推论 \(4.1\) 对于给定的连通平面图,其所有平面嵌入有相同的面数。
推论 \(4.2\) 若 \(G\) 是 \(\nu \ge 3\) 的连通简单平面图,则 \(\varepsilon \le 3\nu-6\)。
证明
由于 \(2\varepsilon = \sum\limits_{f \in F(G)} \deg(f) \ge 3 \phi\)。
故 \(\varepsilon = \nu +\phi-2\),\(\dfrac{1}{3} \varepsilon \le \varepsilon - \phi = \nu-2\),\(\varepsilon \le 3\nu -6\)。
推论 \(4.3\) 若 \(G\) 是连通简单平面图,则 \(\delta \le 5\)。
推论 \(4.4\) \(K_5\) 是非平面图。
推论 \(4.5\) \(K_{3,3}\) 是非平面图。
极大平面图
定义 \(4.3\) 设 \(G\) 是 \(\nu \ge 3\) 的平面图,若任给 \(u,v\in V(G)\),当 \(uv \notin E(G)\) 时,\(G+uv\) 都不再是平面图,则称 \(G\) 是极大平面图。
定理 \(4.5\) \(\nu \ge 3\) 的平面图 \(G\) 是极大平面图,当且仅当 \(G\) 的平面嵌入的每个面都是三角形。
推论 \(4.6\) 假定 \(G\) 是 \(\nu \ge 3\) 的平面图,则 \(G\) 是极大平面图,当且仅当 \(\varepsilon= 3\nu -6\)。
定理 \(4.6\) 若 \(G\) 是 \(\nu \ge 4\) 的极大平面图,则 \(\delta \ge 3\)。
可平面图的判定
给定两个图 \(G\) 和 \(H\),如果通过一系列如下的两种变换可以将 \(G\) 变成 \(H\),则称 \(G\) 与 \(H\) 同胚。
\((1)\) 在 \(G\) 的边上插入度数为 \(2\) 的顶点,将原来的一条边变成两条边。
\((2)\) 将 \(G\) 中度数为 \(2\) 的顶点去掉,将该顶点关联的两条边连成一条边。
定理 \(4.7\) 图 \(G\) 是平面图,当且仅当 \(G\) 中不含与 \(K_5\) 或 \(K_{3,3}\) 同胚的子图。
给定图 \(G\) 中的一条边 \(e=uv \in E(G)\),图 \(G\) 对 \(e\) 的收缩 \(G \cdot e\) 是指:删去边 \(e\) 及端点 \(u\) 和 \(v\),增加一个新顶点 \(w\),将 \(w\) 与 \(u\) 和 \(v\) 的每个邻顶连一条边。形象地说,就是将边 \(e\) 的长度收缩为零。
\(\text{Kuratowsky}\) 定理可改写为:图 \(G\) 是平面图当且仅当 \(G\) 中不含能收缩为 \(K_5\) 和 \(K_{3,3}\) 的子图。
电路制版的时候,为防止出现短路等错误,每一层都是平面嵌入,但实际需要部署的电路通常都是非平面图,为此就需要将电路分层部署,而且为了成本等原因还要使层数尽量少。转换为图论问题就是:如果一个图不是平面图,可以把它的边嵌入多个平面,使每个平面上的边只在端点处相交,即把图 \(G\) 的边集划分为 \(E(G) = \bigcup\limits_{i=1}^n E_i, E_i \cap E_j = \varnothing, i \ne j\),且每个边导出子图 \(G[E_i](i = 1,2,\cdots,n)\) 都是平面图。\(n\) 的最小值称为图 \(G\) 的厚度,记为 \(\theta(G)\)。
定理 \(4.8\) 对 \(\nu(\ge 3)\) 阶简单图 \(G\) 的厚度 \(\theta(G)\),有以下估计式:
\((1)\) \(\theta \ge \left\lceil \dfrac{\varepsilon}{3\nu -6} \right\rceil\);
\((2)\) 若连通图 \(G\) 中没有 \(3\) 阶圈,则 \(\theta(G)\ge \left\lceil \dfrac{\varepsilon}{2\nu -4} \right\rceil\);
\((3)\) \(θ(K_\nu)\ge \left\lfloor \dfrac{\nu+7}{6} \right\rfloor\)。
习题
\(4.1.\) 证明:\(K_5\) 与 \(K_{3,3}\) 删去一条边后都是平面图。
\(4.2.\) 试写出五面体的顶点数和棱数。
\(4.3.\) 关于平面图。
\((1)\) 证明:若 \(G\) 是 \(\nu >11\) 的简单平面图,则 \(G^c\) 不是平面图。
\((2)\) 试给出一个 \(\nu=8\) 的简单平面图,使得 \(G^c\) 是平面图。
解答
\((1)\) 反证,假设存在某个 \(G\) 使得 \(G^c\) 是平面图,则 \(\varepsilon(G) + \varepsilon(G^c) \le 6 \nu -12 < \dfrac{\nu(\nu-1)}{2}\),矛盾。
\(4.4.\) 设连通平面图 \(G\) 是有 \(8\) 个顶点的 \(4\)-正则图,则它的平面嵌入把平面分成多少个面?
解答
\(\nu-\varepsilon+\phi=2\),\(\phi=10\)。
\(4.5.\) 设 \(\omega\) 是平面图 \(G\) 的连通片个数,则 \(\nu(G)-\varepsilon(G)+\phi(G)=\omega+1\)。
解答
对 \(\omega\) 归纳,当 \(\omega=1\) 时显然成立。当 \(\omega>1\) 是找到一个连通片 \(G'\),\(G'\) 与 \(G-G'\) 共用外部面,有 \(\nu(G)-\varepsilon(G)+\phi(G)=(\omega -1 +1) + 2 -1=\omega+1\)。
\(4.6.\) 设 \(G\) 是连通的简单平面图,面数 \(\phi<12\),最小度 \(\delta \ge 3\)。
\((1)\) 证明 \(G\) 中存在度数小于等于 \(4\) 的面。
\((2)\) 举例说明当 \(\phi=12\) 时,其他条件不变,\((1)\) 的结论不成立。
解答
\((1)\) \(-\dfrac12\nu +11 \ge\nu - \varepsilon + \phi=2\),\(\nu \le 18,\dfrac{3}{2} \nu \le \varepsilon = \nu + \phi -2,\phi \ge \dfrac{1}{2} \nu+2\)。
记面的最小度数为 \(k\),有 \(k \le \dfrac{2\varepsilon}{\phi} = 2+\dfrac{2\nu-4}{\phi} \le 2+ \dfrac{32}{11} <5\),也就是说 \(k \le 4\)。
\((2)\) 正十二面体的平图。
\(4.7.\) 设 \(G\) 是 \(\nu\) 个顶点 \(\varepsilon\) 条边的简单平面图,\(\varepsilon<30\),证明存在顶点 \(v\in V(G)\),使得 \(\deg(v) \le 4\)。
解答
上题的对偶版本,证明相似,留给读者思考。
\(4.8.\) 对于平面图 \(G\)。
\((1)\) 证明:若 \(G\) 是围长(即最短圈的长度)\(k \ge 3\) 的连通平面图,则 \(\varepsilon \le \dfrac{k(\nu-2)}{k-2}\)。
\((2)\) 利用 \((1)\) 证明:\(\text{Petersen}\) 图是非平面图。
解答
\((1)\) \(\dfrac{k(\nu-2)}{k-2}=\dfrac{k(\varepsilon-\phi)}{k-2}=\varepsilon+\dfrac{2\varepsilon-k\phi}{k-2} \ge \varepsilon\)。
\((2)\) 套公式即可。
\(4.9.\) 试证正多面体只有五种,且计算出它们的顶点数、棱数和面数。
解答
记每个点度数为 \(d\),每个面度数为 \(k\)。
有 \(d\nu=k\phi=2\varepsilon\),则 \(2=\varepsilon(\dfrac{2}{d}-1+\dfrac{2}{k})\),也就是 \(\dfrac{1}{\varepsilon}+\dfrac{1}{2}=\dfrac{1}{d}+\dfrac{1}{k}\),注意到 \(d,k \ge 3\) 且 \(\dfrac{1}{2}<\dfrac{1}{d}+\dfrac{1}{k}\),枚举后只有 \((3,3),(3,4),(3,5),(4,3),(5,3)\) 五组解。
\(4.10.\) 设 \(G\) 是 \(\nu\) 个顶点 \(\varepsilon\) 条边的简单连通平面图,\(\nu=7,\varepsilon=15\),证明:\(G\) 的所有面的度数都是 \(3\)。
\(4.11.\) 一个连通平面图是 \(2\)-连通的,当且仅当它的每个面的边界都是圈。
解答
若存在边界不是圈,那么有割边或割顶,那么 \(\kappa \le 1\) 或 \(\kappa\le \kappa' \le 1\)。
若一个连通平面图不是 \(2\)-连通的,那么存在割顶,那么包含割顶的面不是圈。
\(4.12.\) 证明:在 \(\nu \ge 7\) 的连通平面图上可以选取不超过 \(5\) 个顶点,把它们删除后得到的图不
连通。
解答
\(\kappa \le \delta \le 5\),找到最小顶割集即可。
\(4.13.\) 设 \(G\) 是连通的 \(3\)-正则平面图,\(\phi_i\) 是 \(G\) 中度数为 \(i\) 的面的个数,证明:\(12 = 3 \phi_3 +2 \phi_4 + \phi_5 -\phi_7 -2\phi_8 -3\phi_9 -\cdots\)。
解答
注意到 \(2\varepsilon=3\nu\),那么 \(12=6\phi-2\varepsilon=6(\phi_3+\phi_4+\cdots)-(3\phi_3+4\phi_4+\cdots)=3 \phi_3 +2 \phi_4 + \phi_5 -\phi_7 -2\phi_8 -3\phi_9 -\cdots\)。
\(4.14.\) 证明图 \(G\) 不是平面图。
\(4.15.\) 画出所有 \(6\) 阶连通的简单非同构的非平面图。
\(4.16.\) 证明 \(K_{3,3}\) 的厚度是 \(2\)。
\(4.17.\) 求图 \(G\) 的厚度。
\(4.18.\) 试证:\(\theta(K_\nu) \ge \left\lceil \dfrac{\nu(\nu -1)}{6(\nu -2)}\right\rceil\)。并证明:等式对所有 \(\nu \le 8\) 成立(参考本章习题 \(4.3.(2)\))。
\(4.19.\) 证明:当 \(m\) 和 \(n\) 不同时为 \(1\) 时,\(K_{m,n}\) 的厚度至少是 \(\left\lceil \dfrac{mn}{2m+2n-4} \right\rceil\)。
\(4.20.\) 设 \(S =\{x_1,x_2,\cdots,x_n\}\) 是平面上 \(n\) 个点的集合,\(n \ge 3\),其中任何两点之间的距离至少是 \(1\)。证明:最多有 \(3n-6\) 个点对,其距离恰好是 \(1\)。
解答
不难观察到距离为 \(1\) 的点两两连边后 \(K_{3,3}\) 和 \(K_5\) 都不存在,那么直接规约为平面图。
匹配理论
两个例子
设某公司有员工 \(x_1,x_2,\cdots,x_m\),有一些工作 \(y_1,y_2,\cdots,y_n\) 需要分配给这些员工。通常一个员工只适合做某些工作,而不适合做另外一些工作。工作分配的原则是每个人只能做一份工作,每一份工作也只能一个人来做。那我们能够给出一个工作分配方案,使得每个人都有工作且每份工作都有人去做吗?若做不到,那最多能够使得多少员工有工作,多少份工作有人做呢?
设有一个残缺的 \(m\times n\) 棋盘,我们用 \(1\times 2\) 的多米诺骨牌来覆盖,要求:\(1.\) 骨牌不能覆盖残缺的位置;\(2.\) 骨牌间不能有重叠。问能否将所有非残缺的位置都覆盖到?若不能覆盖所有残缺的位置,最多能够覆盖多少张牌?
匹配的定义
定义 \(5.1\) 设 \(M\) 是图 \(G\) 的边子集,且 \(M\) 的任意两条边在 \(G\) 中都不相邻,则称 \(M\) 是 \(G\) 的一个匹配。\(M\) 中同一条边的两个端点称为在 \(M\) 中相配。\(M\) 中边的端点称为被 \(M\) 许配。若 \(G\) 中所有的顶点都被 \(M\) 许配,则称 \(M\) 是 \(G\) 的完备匹配。\(G\) 中边数最多的匹配称为 \(G\) 的最大匹配。若 \(M\) 是 \(G\) 的最大匹配,则称 \(M\) 中的边数 \(|M|\) 为 \(G\) 的匹配数,记作 \(\alpha(G)=|M|\)。
定义 \(5.2\) 设 \(M\) 是图 \(G\) 的匹配,\(P =v_0e_1v_1e_2\cdots e_kv_k\) 是 \(G\) 中的一条轨道(圈),若 \(e_1,e_2,\cdots,e_k\) 在 \(M\) 与 \(E(G)-M\) 中交替出现,则称 \(P\) 是 \(G\) 中关于 \(M\) 的交错轨道(圈)。
定义 \(5.3\) 设 \(P=v_0e_1v_1e_2\cdots e_{2k+1}v_{2k+1}\) 是 \(G\) 中关于 \(M\) 的交错轨道,若 \(e_1, e_3, \cdots ,e_{2k+1} \notin M, e_2,\cdots ,e_{2k} \in M\),且 \(v_0\) 与 \(v_{2k+1}\) 没有被 \(M\) 许配,则称 \(P\) 是 \(G\) 中关于 \(M\) 的可增广轨道。
引理 \(5.1\) \(M\) 是 \(G\) 的最大匹配,当且仅当 \(G\) 中没有关于 \(M\) 的可增广轨道。
证明
定义对称差 \(G=X\oplus Y\),表示 \(e \in E(G)\) 当且仅当 \(e\in E(X)\) 和 \(e \in E(Y)\) 恰好满足一个。
充分和必要均反证,考虑若存在关于匹配 \(M\) 的可增广轨道 \(P\),那么匹配 \(M'=M\oplus P\) 满足 \(|M'|=|M|+1\),与最大匹配矛盾。
若匹配 \(M\) 不是最大匹配,考虑找到最大匹配 \(M'\),那么考虑 \(G'=M \oplus M'\),在 \(G'\) 中每个点的度数为 \(1\) 或 \(2\),且在 \(M'\) 中的边比在 \(M\) 中的边多,那么一定存在一条轨道上在 \(M'\) 中的边比在 \(M\) 上的边数多,与无可增广轨道矛盾。
二分图中的匹配
定理 \(5.1\text{(Hall)}\) 设 \(G\) 是二分图,其顶点集合划分为 \(V(G) = X\cup Y\),\(X \cap Y = \varnothing\),则 \(G\) 中存在将 \(X\) 中顶点都许配的匹配,当且仅当任给 \(S \subseteq X\),都有 \(|N(S)|\ge |S|\)。其中,\(N(S)\) 是与 \(S\) 中顶点相邻的顶点构成的集合,简称为 \(S\) 的邻顶集合。
证明
假设存在将 \(X\) 全部许配的匹配 \(M\),那么对于任意 \(S \subseteq X\),\(S\) 中顶点均许配给 \(N(S)\) 中顶点,故需满足 \(|N(S)| \ge |S|\)。
假设任给 \(S \subseteq X\),都有 \(|N(S)|\ge |S|\)。考虑最大匹配 \(M\),若存在 \(u \in X\),\(u \notin M\),考虑与 \(u\) 之间有交错轨道的顶点构成的集合 \(Z\),令 \(S=Z \cap X\),\(T=Z \cap Y\),\(Z\) 中只有 \(u\) 未被许配,故有 \(|S|=|T|-1\),而显然 \(N(S) \subseteq Z\),那么此时推出矛盾,故 \(\text{Hall}\) 定理成立。
\(\text{Hall}\) 定理也称为婚配定理。
推论 \(5.1\) 对于正整数 \(k>0\),\(k\) 次正则二分图 \(G\) 有完备匹配。
定义 \(5.4\) 设 \(G\) 是一个图,\(C\) 是其顶点集合的子集,即 \(C \subseteq V(G)\),若 \(G\) 中任意一条边都有一个端点属于 \(C\),则称 \(C\) 是 \(G\) 的一个覆盖。若 \(C\) 是 \(G\) 的覆盖,但 \(C\) 的任何真子集都不是 \(G\) 的覆盖,则称 \(C\) 是 \(G\) 的极小覆盖。若 \(C^*\) 是 \(G\) 的覆盖,且不存在 \(G\) 的覆盖 \(C\),使得 \(|C|<|C^*|\),则称 \(C^*\) 是 \(G\) 的最小覆盖,且称 \(|C^*|\) 是 \(G\) 的覆盖数,记作 \(\beta(G)\)。
引理 \(5.2\) 假设 \(C\) 是图 \(G\) 的覆盖,\(M\) 是图 \(G\) 的匹配,则 \(|C| \ge |M|\)。
证明
注意该引理在一般图情况下均成立。
考虑一组匹配 \(M=\{e_1,e_2,\cdots,e_n\}\),由于 \(C\) 是覆盖,则 \(e_i=u_iv_i\) 必有一点(令是 \(u_i\))在 \(C\) 中,而 \(u_i\) 互不相同,故 \(|C|\ge |M|\)。
引理 \(5.3\) 若图 \(G\) 存在覆盖 \(C\) 和匹配 \(M\),使得 \(|C|=|M|\),则 \(C\) 是最小覆盖,\(M\) 是最大匹配。
证明
显然 \(|M|\le |M^*| \le |C^*| \le |C|\),\(|M|=|C|\) 只能全部取等。
定理 \(5.2\text{(König-Egerváry)}\) 设 \(G\) 是二分图,则 \(G\) 的匹配数等于其覆盖数,
即 \(\alpha(G)=\beta(G)\)。
证明
设 \(V=X \cup Y\),若存在一个匹配包含 \(X\) 中所有点,那么覆盖直接选 \(X\) 就得证。
否则我们考虑 \(X\) 中没有在 \(M\) 中出现的点,记为 \(U\),找到与 \(U\) 中任意一点有交错轨道的集合 \(Z\),令 \(S=Z \cap X\),\(T=Z \cap Y\),显然 \(Z\) 中只有 \(U\) 未被许配,此时匹配数为 \(|T|\),同时覆盖选择 \(T\) 即可满足匹配数等于覆盖数。
剩余部分 \(X-S\) 中的点均被许配,直接选择 \(X-S\) 即可。此时匹配数和覆盖数均为 \(|X|-|S|+|T|\)。
任意图的完备匹配
定义 \(5.5'\) 设 \(G'\) 是图 \(G\) 的连通片,若 \(\nu(G')\) 是奇数,则称 \(G'\) 是 \(G\) 的奇片。否则,称之为 \(G\) 的偶片。我们用 \(o(G)\) 表示 \(G\) 中奇片的个数。
定理 \(5.3\text{(Tutte)}\) \(G\) 有完备匹配,当且仅当任给 \(S \subseteq V(G)\),都有 \(o(G-S) \le |S|\)。
证明
必要性显然,否则 \(o(G-S)\) 总会有一个奇片的多余点无法匹配。
充分性有些复杂,感兴趣的读者可以自行证明。
定理 \(5.4\text{(Petersen)}\) 无桥的三次正则图有完备匹配。
证明
任取点集 \(S\),考虑 \(G-S\) 中所有奇片 \(G_1,G_2,\cdots,G_k\)。
对于奇片 \(G_i\),考虑其与 \(S\) 中的连边数,记为 \(m_i\),显然 \(m_i=\sum\limits_{u \in V(G_i)} \deg(u)-2\varepsilon(G_i)=3\nu(G_i)-2\varepsilon(G_i)\)。
由于没有割边,\(m_i\ge 2\),而由于 \(\nu(G_i)\) 是奇数,那么 \(m_i\) 也是奇数,\(m_i \ge 3\)。
那么 \(3|S| \ge \sum\limits_{i=1}^k m_i \ge 3k\),故 \(|S|\ge o(G-S)\),满足 \(\text{Tutte}\) 定理。
最大匹配算法
这里使用 \(\text{OI-wiki}\) 中的内容。
最佳匹配算法
这里使用 \(\text{OI-wiki}\) 中的内容。
习题
\(5.1.\) 求 \(K_{2n}\) 与 \(K_{n,n}\) 中不同的完备匹配的个数。
\(5.2.\) 证明:树至多有一个完备匹配。
解答
假设树有至少一个完备匹配 \(M\)。
首先 \(\nu\) 是偶数,而任取 \(v\),\(T-v\) 有 \(\deg(v)\) 个连通片,且至少有一个奇片。
由于我们假设树有完备匹配,那么假设 \(uv \in E\),\(v\) 所在连通片是奇片,那么一定有 \(uv \in M\)。
也就是说和 \(v\) 许配的点固定,完备匹配 \(M\) 确定。
\(5.3.\) 对于 \(k>1\),给出没有完备匹配的 \(k\) 次正则图的例子。
解答
奇圈。
\(5.4.\) 两个人在图 \(G\) 上博弈,交替选择不同的顶点 \(v_0,v_1,v_2,\cdots,\) 使得当 \(i>0\) 时,\(v_i\) 与 \(v_{i-1}\) 相邻,直到不能选到顶点为止,谁最后能选到一个顶点谁赢。证明:第一个选顶点的人有必胜的策略,当且仅当 \(G\) 中无完备匹配,并给出一个必胜的策略。
解答
若存在完备匹配,则每次先手选择 \(u\) 后手选择 \(u\) 许配的点即可。
显然所有点都有许配点,所以后手总能找到应对策略。
若不存在完备匹配,则先手选择一个不在最大匹配中的点 \(v\),然后后手每次选择 \(u\),先手都选择 \(u\) 许配的点即可。
对于后手第一次选择,由于先手选的点不在最大匹配中,所以后手第一次选的点一定在最大匹配中。
然后后手每一步都不可能走出最大匹配,否则就找到了先手第一次选的点和这次选的点之间的一条可增广轨,与最大匹配矛盾。
\(5.5.\) \(G\) 的一个 \(k\) 度因子是指 \(G\) 的一个 \(k\) 次正则生成子图。\(G\) 的 \(k\) 度因子分解是将 \(G\) 分解成一些无公共边的 \(k\) 度因子之并,即 \(\bigcup\limits_{i=1}^n H_i\),其中 \(H_i(1 \le i \le n)\) 是 \(G\) 的 \(k\) 度因子。证明:
\((1)\) \(K_{2n}\) 与 \(K_{n,n}\) 是可 \(1\) 度因子分解的。
\((2)\) \(\text{Petersen}\) 图是不能 \(1\) 度因子分解的。
解答
\((1)\) 以 \(n=3\) 为例。


\((2)\) 显然每次都连奇数条内-外边,只能 \(1,1,3\) 分配,肯定分不上。
\(5.6.\) 证明:\(8\times 8\) 的正方形去除对角上的两个 \(1\times 1\) 的小正方形后,不能用 \(1\times 2\) 的长方形覆盖。
解答
黑白染色(按国象棋盘染色)例题。
\(5.7.\) 证明:二分图 \(G\) 有完备匹配的充要条件是,对任何 \(S\subseteq V(G)\),都满足 \(|N(S)| \ge |S|\)。这个命题对一般图成立吗?
解答
不成立,奇圈。
\(5.8.\) 对于 \(k>0\),证明:
\((1)\) 每个 \(k\) 次正则二分图都是可以 \(1\) 度因子分解的。
\((2)\) 每个 \(2k\) 次正则图都是可以 \(2\) 度因子分解的。
解答
\((1)\) 每次找到一个完备匹配 \(M\),然后归纳到 \(k-1\) 的子问题。
\((2)\) 把 \(2k\) 个 \(1\) 度因子两两合并即可。
\(5.9.\) 矩阵的一行或一列称为矩阵的一条线。证明:\(0\)-\(1\) 矩阵中包含所有 \(1\) 所需的最少线数等于没有两个 \(1\) 在同一条线上的 \(1\) 的最大个数。
解答
考虑矩阵 \((a_{ij})_{m \times n}\),建立一张二分图 \(G\),\(X\) 中的点对应 \(m\) 行,\(Y\) 中的点对应 \(n\) 列。若 \(a_{ij}=1\),那么给行 \(i\) 和列 \(j\) 之间连接一条边,表示第 \(i\) 行的线和第 \(j\) 列的线之间必选至少一条。
那么 \(G\) 的最大匹配表示最多的边使得点不重复,也就是没有两个 \(1\) 在同一条线上的 \(1\) 的最大个数。
\(G\) 的最小覆盖表示选一些点包含所有边,也就是包含所有 \(1\) 所需的最少线数。
最大匹配数等于最小覆盖数,结论成立。
\(5.10.\) 设 \(A=(a_{ij})_{m\times n}\) 是一个 \(0\)-\(1\) 矩阵,\(m\le n\)。矩阵 \(A\) 的每一行都有 \(k\) 个 \(1\),而每一列 \(1\) 的个数不超过 \(k\) 个,则 \(A\) 可以表示成 \(A=P_1+P_2+\cdots+P_k\),其中 \(P_i(1\le i\le k)\) 也是 \(m\times n\) 阶 \(0\)-\(1\) 矩阵,而且每行恰有一个 \(1\),每列中 \(1\) 的个数不超过一个。
解答
模型同上题,每次找到最大匹配每一行所对应的点必定都选,然后可以归纳。
\(5.11.\) 设 \(G\) 是顶点集合划分为 \(X\) 与 \(Y\) 的二分图,则 \(G\) 的最大匹配中的边数等于 \(|X|- \max\limits_{S\subseteq X}\{|S| -|N(S)|\}\)。
解答
证明同 \(\text{Hall}\) 定理,反证即可。
\(5.12.\) 用 \(\text{König-Egerváry}\) 定理来证明 \(\text{Hall}\) 定理。
解答
考虑证明 \(\alpha=\beta=|X|\) 当且仅当任给 \(S \subseteq X\),\(|N(S)| \ge |S|\)。
若 \(\alpha \ne |X|\),则 \(\beta \ne |X|\),考虑找到一个最小覆盖集 \(T\),令 \(S=X-(T \cap X)\),也就是说 \(S\) 是 \(X\) 中不在 \(T\) 中的点。此时显然有 \(N(S) \subseteq T\),且由于 \(T\) 最小,所以 \(|N(S)|<|S|\)。
若 \(|N(S)|<|S|\),那么根据 \(\text{König-Egerváry}\) 定理的证明方法可以直接得到 \(\beta \ne |X|\)。
\(5.13.\) 用 \(\text{Tutte}\) 定理来证明 \(\text{Hall}\) 定理。
解答
若 \(|X|,|Y|\) 奇偶性不同,\(Y \leftarrow Y \cup \{y_0\}\)。将 \(Y\) 连成完全图,记新图为 \(H\)。
原图有包含 \(X\) 中所有顶点的匹配 \(\Longleftrightarrow\) 新图有完备匹配。
充分性:任取 \(S \subseteq X\),若 \(o(H-N(S)) \le |N(S)|\),由于 \(H-N(S)\) 都是孤立点,\(|S|\le o(H-N(S)) \le |N(S)|\)。
必要性:若存在 \(T\),\(o(H-T)>|T|\)。
若 \(Y \subseteq T\),显然 \(|X|>|N(X)|\)。
否则考虑 \(T'=T \cap Y\),若 \(T'=T\),显然 \(o(H-T') >|T'|\),否则 \(o(H-T')\ge o(H-T)-1\ge |T|>|T'|\)。
\(H-T'\) 会被分为与 \(Y-T\) 连通的部分(最多一个奇片)和剩余 \(X\) 中的孤立点(记为 \(S\),最多 \(|S|\))个奇片。
显然 \(|S|\ge o(H-T')-1\ge |T'|\),若 \(|S|=|T'|\),那么与 \(Y-T'\) 连通的部分大小为偶数,有 \(|S|>|T'|\),矛盾。故 \(|S|>|T'|\ge |N(S)|\)。
\(5.14.\) 证明:若 \(G\) 是 \(k-1\) 边连通的 \(k\) 次正则图,且 \(\nu(G)\) 是偶数,则 \(G\) 有完备匹配。
解答
反证,若存在 \(S \subseteq V\),\(o(G-S)>|S|\)。考虑所有奇片 \(G_i\),由于 \(G\) 是 \(k-1\) 边连通的,\(V(G_i)\) 与 \(S\) 之间的连边至少有 \(k\) 条。而有一端在 \(S\) 中的边之多有 \(|S|k\) 条,故 \(o(G-S)k\le |S|k\),矛盾。
\(5.15.\) 证明:树 \(T\) 有完备匹配,当且仅当对任意 \(v\in V(T)\),都有 \(o(T -v)=1\)。
解答
同 \(5.2.\),可以直接构造出完备匹配。
\(5.16.\) 由 \(a,b,c,d,e,f\) 六个人组成检查团,检查 \(5\) 个单位的工作。若某单位与某人有过工作联
系,则不能选派此人到该单位去检查工作。已知第一单位与 \(b,c,d\) 有过联系,第二单位与 \(a,e,f\),第三单位与 \(a,b,e,f\),第四单位与 \(a,b,d,f\),第五单位与 \(a,b,c\) 有过联系,请列出去各个单位进行检查的人员名单。
\(5.17.\) 设有四个人 \(A,B,C,D\),有四份工作 \(a,b,c,d\),每个人做某份工作的效率如下面的矩阵所
示,试求最佳的工作分配方案。
\(5.18.\) 从 \(8\times 8\) 的棋盘上选 \(16\) 个格子,其中每行每列选两个格子。证明:可以将 \(8\) 个白子、\(8\) 个黑子放在所选的格子上,使每行每列恰有一个白子、一个黑子。
解答
将行或列相同的格子中间连边,容易证明图中无奇圈,故是二分图,将 \(X\) 全放白子,\(Y\) 全放黑子即可。
\(5.19.\) 证明:\(\text{Kuhn-Munkreas}\) 算法中修改顶标后,\(\hat{l}\) 仍然是可行顶标。
解答
若 \(x \notin S\) 或 \(y \in T\),那么显然 \(\hat{l}(x)+\hat{l}(y)\ge l(x)+l(y)\)。
若 \(x \in S\) 且 \(y \in T\),由于 \(\alpha \le l(x)+l(y)-w(xy)\),故 \(\hat{l}(x)+\hat{l}(y)=l(x)+l(y)-\alpha\ge w(xy)\)。
\(5.20.\) \(\text{Kuhn-Munkreas}\) 算法中修改顶标后,由可行顶标 \(\hat{l}\) 得到相等子图 \(G_{\hat{l}}\)。证明:在算法的第 \((3)\) 步,在 \(G_{\hat{l}}\) 上找到的顶点子集 \(T\) 包含了在 \(G_l\) 上找到的顶点子集 \(T\),且至少多一个顶点。 由此可知,\(\text{Kuhn-Munkreas}\) 算法最终能够找到某个相等子图,该相等子图有完备匹配,从而说明 \(\text{Kuhn-Munkreas}\) 算法的正确性。
解答
不难证明一定会出现至少一条新的交错轨道。
Euler 图与 Hamilton 图
Euler 图
定义 \(6.1\) 经过图 \(G\) 每条边的行迹称为 \(\text{Euler}\) 迹;经过图 \(G\) 每条边的闭行迹称为 \(\text{Euler}\) 回路。如果图 \(G\) 含有 \(\text{Euler}\) 回路,则称 \(G\) 为 \(\text{Euler}\) 图。
定理 \(6.1\) 设 \(G\) 是连通图,则下面三个命题等价:
\((1)\) \(G\) 是 \(\text{Euler}\) 图;
\((2)\) \(G\) 的每个顶点的度数都是偶数;
\((3)\) \(G\) 可以表示成无公共边的圈之并。
证明
只需证明 \((1) \Rightarrow (2) \Rightarrow (3) \Rightarrow (1)\)。
\((1) \Rightarrow (2)\):显然 \(\text{Euler}\) 回路上 \(v\) 每次出现两侧均是与 \(v\) 关联的不同的边,故若 \(v\) 出现 \(k\) 次有 \(\deg(v)=2k\)。
\((2) \Rightarrow (3)\):首先 \(G\) 不是树,故可以每次拿出一个圈然后归纳。
\((3) \Rightarrow (1)\):考虑每次合并两个点相交的闭行迹,由于连通一定能找到,然后可以归纳得到一个 \(\text{Euler}\) 回路。
推论 \(6.1\) 连通图 \(G\) 有 \(\text{Euler}\) 迹,当且仅当 \(G\) 中最多有两个度数为奇数的顶点。
定理 \(6.2\) 设 \(D\) 是有向图,且略去 \(D\) 中边的方向后,对应的无向图连通,则下面三个命题等价:
\((1)\) \(D\) 是 \(\text{Euler}\) 图;
\((2)\) \(\forall v \in V(D)\),\(\deg^+(v) = \deg^-(v)\);
\((3)\) \(D\) 可以表示成无公共边的有向圈之并。
推论 \(6.2\) 连通有向图 \(D\) 有 \(\text{Euler}\) 有向迹但不是有向 \(\text{Euler}\) 图,当且仅当 \(D\) 中恰有两个度数为奇数的顶点,其中一个顶点入度比出度大 \(1\),另一个的出度比入度大 \(1\),其余顶点的入度均等于出度。
关于 \(\text{Euler}\) 回路的求法,这里使用 \(\text{OI-wiki}\) 中的内容。
中国邮递员问题
构造无向加权图 \(G=(V,E,w)\),\(E\) 为街道集合,\(V\) 中的元素是街道的交叉点,街道的长度为该街道对应的边的权,显然所有权均为正数。这样,邮递员问题就变成了求 \(G\) 中一条经过每条边至少一次的回路 \(C\),使该回路的权 \(\sum\limits_{e\in E(C)} w(e)\) 最小,且称满足以上条件的回路是最优投递路线。
\(\text{Edmonds-Johnson}\) 算法的思路是考虑若图是 \(\text{Euler}\) 图,那么显然 \(\text{Euler}\) 回路即为答案,否则考虑通过对所有奇度数的点找到最小权最大匹配即可转化为 \(\text{Euler}\) 图。
Hamilton 图
定义 \(6.2\) 经过图 \(G\) 每个顶点的轨道称为 \(\text{Hamilton}\) 轨道;经过图 \(G\) 每个顶点的圈称为 \(\text{Hamilton}\) 圈。如果图 \(G\) 含有 \(\text{Hamilton}\) 圈,则称这个图为 \(\text{Hamilton}\) 图。
规定平凡图是 \(\text{Hamilton}\) 图。
定理 \(6.4\) 设 \(G\) 是 \(\text{Hamilton}\) 图,则对 \(V(G)\) 的每个非空真子集 \(S\),均有 \(\omega(G-S) \le |S|\)。
证明
考虑 \(\text{Hamilton}\) 圈 \(H\),显然有 \(\omega(G-S)\le \omega(H-S) \le |S|\)。
定理 \(6.5\text{(Dirac)}\) 设 \(G\) 是简单图,且 \(\nu(G) \ge 3\),\(\delta(G) \ge \dfrac{\nu(G)}2\),则 \(G\) 是 \(\text{Hamilton}\) 图。
证明
反证,加一些边得到一个极大的非 \(\text{Hamilton}\) 图 \(G'\),显然 \(G'\) 不是完全图。记 \(uv \notin E(G')\),考虑 \(G'+uv\) 是 \(\text{Hamilton}\) 图,那么 \(G'\) 中存在以 \(u\) 为起点,\(v\) 为终点的 \(\text{Hamilton}\) 轨道,记为 \(w_1=u,w_2,\cdots,w_\nu=v\)。
令 \(S=\{w_i|uw_{i+1} \in E(G')\}\),\(T=\{w_i|vw_i \in E(G')\}\)。由于 \(\delta(G') \ge \delta(G) \ge \dfrac{\nu}{2}\),故 \(S \cap T \ne \varnothing\)。
考虑 \(w_i \in S \cap T\),那么 \(w_1w_2\cdots w_iw_\nu w_{\nu-1}\cdots w_{i+1}w_1\) 是 \(G'\) 中的 \(\text{Hamilton}\) 回路,矛盾。
引理 \(6.1\) 设 \(G=(V,E)\) 是简单图,\(u\) 和 \(v\) 是 \(G\) 中两个不相邻的顶点,且 \(\deg(u) + deg(v) \ge \nu(G)\),那么 \(G\) 是 \(\text{Hamilton}\) 图,当且仅当 \(G+uv\) 是 \(\text{Hamilton}\) 图。
\(G\) 的闭包 \(c(G)\) 指的是用下述方法从 \(G\)得到的一个图:反复连接 \(G\) 中度数之和不小于 \(\nu(G)\) 的不相邻顶点对,直到没有这样的顶点对为止。
引理 \(6.2\) \(c(G)\) 唯一确定。
证明
反证,考虑两个不同的闭包 \(G_1,G_2\),令 \(|E(G_1)|\le |E(G_2)|\),在构造 \(G_2\) 时第一条不在 \(G_1\) 中的新加入的边为 \(u,v\),记此时图为 \(G'\)。
有 \(\deg_{G_1}(u)+\deg_{G_1}(v) \ge \deg_{G'}(u)+\deg_{G'}(v) \ge \nu\),那么 \(uv \in E(G_1)\),矛盾。
定理 \(6.6\) 简单图 \(G\) 是 \(\text{Hamilton}\) 图,当且仅当它的闭包 \(c(G)\) 是 \(\text{Hamilton}\) 图。
推论 \(6.3\) 设 \(G\) 是 \(\nu(G) \ge 3\) 的简单图,若 \(c(G)\) 是完全图,则 \(G\) 是 \(\text{Hamilton}\) 图。
定理 \(6.7\text{(Ore,1960)}\) 设 \(\nu(G) \ge 3\),对 \(G\) 的任意一对顶点 \(u,v\),若 \(\deg(u)+\deg(v)\ge \nu(G)-1\),则 \(G\) 有 \(\text{Hamilton}\) 轨道;若 \(\deg(u)+\deg(v) \ge \nu(G)\),则 \(G\) 是 \(\text{Hamilton}\) 图。
证明
证明比较复杂,感兴趣的读者可以自行了解。
旅行商问题
一个旅行商访问若干城市,然后回到他出发的地方。给定各城市之间的距离,应该怎样规划路线,使得他访问每个城市恰好一次并回到原出发点,且总路程最短?这就是著名的旅行商问题或货郎担问题。这个问题可以转化为如下的图论问题。
设 \(K_\nu = (V,E,w)\) 是 \(\nu\) 阶完全加权图,各边的权非负,有的边的权可以是 \(+\infty\),求 \(K_\nu\) 中权最小的 \(\text{Hamilton}\) 圈。
目前还没有求解旅行商问题的有效算法,也无法证明其有效算法不存在。可行的办法是寻找近似算法,本节将介绍三种近似算法。
以下算法中均认为图满足三角形不等式,即 \(w(u,v)+w(v,w)\ge w(u,w)\)。
最近邻法即为选择一个顶点 \(v_1\) 作为起点,维护一条轨道 \(W=v_1\cdots v_k\),每次找到 \(v \notin W\) 且 \(w(v_k,v)\) 最小的 \(v\) 放到 \(W\) 的末尾,最后连成圈即可,记权为 \(d\)。
复杂度 \(O(\nu^2)\),但性能不好,记 \(d_0\) 表示 \(G\) 中最短的 \(\text{Hamilton}\) 圈的权,可得 \(\dfrac{d}{d_0} \le \dfrac{1}{2}(\lceil\log n\rceil+1)\)。
最小生成树法即为找到 \(G\) 的一棵最小生成树 \(T\),然后找到最小生成树的一条 \(\text{Euler}\) 回路,然后再将每个点去重(若再回路中出线多次,只保留第一次出线的位置)。这样能得到一条 \(\text{Hamilton}\) 圈。
复杂度 \(O(\nu^2)\),且有 \(\dfrac{d}{d_0} < 2\)。
最小权匹配法在最小生成树法的基础上,通过给 \(T\) 中奇度点构造最小权完备匹配的方式构造权更小的 \(\text{Euler}\) 回路,再将每个点去重。
复杂度 \(O(\nu^3)\),且有 \(\dfrac{d}{d_0} < \dfrac{3}{2}\)。
习题
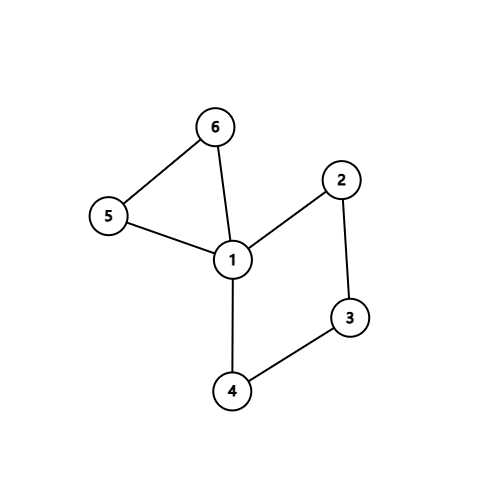
\(6.1.\) \(\text{Herschel}\) 图是否是 \(\text{Euler}\) 图?是否能一笔画?为什么?
\(6.2.\) 如果可能,画出一个 \(\nu\) 为偶数 \(\varepsilon\) 为奇数的 \(\text{Euler}\) 图 \(G\),否则说明为什么不存在这样的图。
解答
存在。
\(6.3.\) 设 \(G\) 是恰有 \(2k\) 个奇度顶点的连通图,证明:\(G\) 中存在 \(k\) 条边不重的行迹 \(P_1,P_2,\cdots,P_k\),使得 \(E(G)=\bigcup\limits_{i=1}^k E(P_i)\)。
解答
记奇度顶点为 \(v_1,\cdots,v_{2k}\),增加 \(v_{2i-1}v_{2i}\) 共 \(k\) 条边,变为 \(\text{Euler}\) 图,找到 \(\text{Euler}\) 回路,将加边删去即可得到 \(k\) 条行迹。
\(6.4.\) 如何将 \(16\) 个二进制数字(\(8\) 个 \(0\),\(8\) 个 \(1\))排成一个圆形,使得 \(16\) 个长为 \(4\) 的二进制数在其中都出现且只出现一次?
\(6.5.\) 如何将 \(9\) 个 \(\alpha\),\(9\) 个 \(\beta\),\(9\) 个 \(\gamma\) 排成一个圆形,使得由这些 \(\alpha,\beta,\gamma\) 产生的 \(27\) 个长为 \(3\) 的符号串在其中都出现且只出现一次?
\(6.6.\) 证明或否定:
\((1)\) 每个 \(\text{Euler}\) 二分图都有偶数条边。
\((2)\) 有偶数个顶点的每个 \(\text{Euler}\) 简单图有偶数条边。
\(6.7.\) 给出一个算法,在有 \(\text{Euler}\) 迹的图中求出一条 \(\text{Euler}\) 迹。
\(6.8.\) 求图 \(G\) 的一条最优投递路线。
\(6.9.\) 设 \(G\) 是二分图,证明:若 \(G\) 是 \(\text{Hamilton}\) 图,则 \(G\) 必有偶数个顶点。\(6.1.\) 中的 \(\text{Herschel}\) 图是 \(\text{Hamilton}\) 图吗?为什么?
解答
反证,若 \(\nu\) 是奇数,\(\text{Hamilton}\) 圈是奇圈,与二分图矛盾。
\(6.10.\) 证明图 \(G_1,G_2\) 两个图都不是 \(\text{Hamilton}\) 图。
\(6.11.\) \(\text{Petersen}\) 图删除一个顶点后是不是 \(\text{Hamilton}\) 图?
\(6.12.\) 求 \(K_n\) 中无公共边的 \(\text{Hamilton}\) 圈的个数。
解答
\(\left\lfloor\dfrac{n-1}{2}\right\rfloor\) 个,具体构造如下。
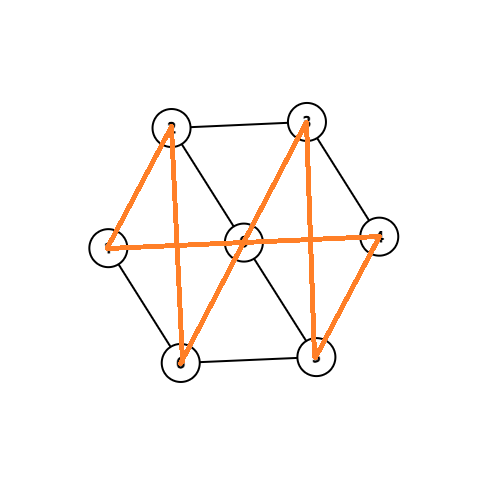
可以旋转 \(\left\lfloor\dfrac{n-1}{2}\right\rfloor\) 次,目前 \(n\) 为奇数且中心点在每条回路中出现两次,删除一次即可得到 \(n\) 为奇数的构造,将其中一个换成新点即可得到 \(n\) 为偶数的构造。
\(6.13.\) 亚瑟王在宫中召见他的 \(2n\) 名骑士,其中某些骑士间互存仇怨,每个骑士的仇人不超过 \(n-1\) 个,则亚瑟王的谋士摩尔林能否让这些骑士围桌就座,使每个骑士不与他的仇人相邻?为什么?
解答
建图,考虑补图 \(G\),有边相连表示没有仇怨,可以相邻,显然 \(G\) 是 \(\text{Hamilton}\) 图,故存在。
\(6.14.\) 证明:\(2k-1\) 阶的 \(k\) 次正则图是 \(\text{Hamilton}\) 图(\(k \ge 2\))。
\(6.15.\) 若图 \(G\) 的任意两个顶点之间有 \(\text{Hamilton}\) 轨道,则称 \(G\) 是 \(\text{Hamilton}\) 连通图,证明:若 \(G\) 是 \(\text{Hamilton}\) 连通图且 \(|V(G)|\ge 4\),则 \(|E(G)| \ge \left\lfloor \dfrac12 (3|V (G)| + 1) \right\rfloor\)。
解答
考虑反证,若 \(\varepsilon < \left\lfloor \dfrac12 (3\nu + 1) \right\rfloor\),不难证明 \(\delta \le 2\)。若存在 \(\deg(u)=1\),考虑 \((u,v) \in E\),那么 \(u,v\) 之间没有 \(\text{Hamilton}\) 轨道,若存在 \(\deg(u)=2\),考虑 \((u,v),(u,w) \in E\),那么 \(v,w\) 之间没有 \(\text{Hamilton}\) 轨道,矛盾。
\(6.16.\) 证明:若 \(G\) 是二分图,但其顶点的划分 \(X\) 与 \(Y\) 不均匀,即 \(|X| \ne |Y|\),则 \(G\) 是不是 \(\text{Hamilton}\) 图。
解答
不妨设 \(|X|>|Y|\)。反证,若存在 \(\text{Hamilton}\) 圈,存在相邻两个点均在 \(X\) 中,与二分图矛盾。
\(6.17.\) 设 \(G\) 是 \(\nu\) 阶无向简单图,边数 \(\varepsilon= \dfrac12 (\nu-1)(\nu-2)+2\)。
\((1)\) 证明:\(G\) 是 \(\text{Hamilton}\) 图。
\((2)\) 举例说明,当 \(\varepsilon= \dfrac12 (\nu -1)(\nu -2)+1\) 时,\(G\) 不一定是 \(\text{Hamilton}\) 图。
\(6.18.\) 给定连通无向图 \(G\)。证明:若 \(G\) 中存在圈 \(C\),删除 \(C\) 上一条边后便是图 \(G\) 的最长轨道,则 \(C\) 是图 \(G\) 的 \(\text{Hamilton}\) 圈。
\(6.19.\) 若围一张圆桌坐着至少 \(6\) 个人,那么一定可以调整他们的位置,使得每个人两侧都挨着新邻居。
解答
考虑补图,显然 \(\delta=\Delta=\nu-3\),那么 \(\forall u,v,\deg(u)+\deg(v)\ge \nu\)。
\(6.20.\) 今有 \(\nu\) 个人,已知他们中的任何两人合起来认识其余的 \(\nu-2\) 人。证明:当 \(\nu \ge 3\) 时,这 \(\nu\) 个人能排成一列,使得中间任何人都认识两边的人,而两头的人认识左边(或右边)的人。当 \(\nu \ge 4\) 时,这 \(\nu\) 个人能排成一个圆圈,使得每个人都认识两边的人。
解答
不难证明 \(\delta\ge \nu-2\)。
\(6.22.\) \(5\) 阶完全加权图如图所示。
\((1)\) 用最近邻法求以 \(a\) 为起点的旅行商问题的近似解。
\((2)\) 用最小生成树法求以 \(a,b\) 为起点的旅行商问题的近似解。
\((3)\) 用最小权匹配法求旅行商问题的近似解。
图的着色
顶点着色
定义 \(7.1\) 图 \(G\) 的一个 \(k\)-顶点着色是指把 \(k\) 种颜色 \(1,2,\cdots ,k\) 分配给图 \(G\) 的顶点,使每个顶点都分配一种颜色;若相邻顶点的颜色不同,则称这种着色是一个正常 \(k\)-顶点着色。若图 \(G\) 有一个正常 \(k\)-顶点着色时,称 \(G\) 是可 \(k\)-顶点着色的。图 \(G\) 的顶点色数指的是使得图 \(G\) 可正常顶点着色的最少颜色数 \(k\),简称为色数,记为 \(\chi (G)\)。色数为 \(k\) 的图是可 \(k\)-顶点着色,但不是可 \((k-1)\)-顶点着色的。
用代数的方式解释,图 \(G\) 的一个正常 \(k\)-顶点着色可以表示为顶点集合 \(V(G)\) 的一个划分 \(\mathcal{C} =(V_1,V_2,\cdots ,V_k)\),其中 \(V_i\) 表示着 \(i\) 色的顶点子集(可能是空集),满足:
\((1)\) \(V(G) = V_1 \cup V_2 \cup \cdots \cup V_k\);
\((2)\) \(V_i \cap V_j = \varnothing,1 \le i \ne j \le k\);
\((3)\) 任给 \(1 \le i \le k\),且任给 \(u,v \in V_i,uv \notin E(G)\)。
在进行正常 \(k\)-顶点着色时,若要求每种颜色都必须用到,则还需满足下面的第 \((4)\) 个条件;否则不需要。
\((4)\) 任给 \(1 \le i \le k,V_i \ne \varnothing\)。
关于顶点着色,有下面的简单性质:
\((1)\) \(\nu\) 阶图的色数满足 \(1 \le \chi(G) \le ν\);\(\chi(G)=1\) 当且仅当 \(G\) 是零图;\(\chi(G) =\nu\) 当且仅当 \(G\) 是 \(\nu\) 阶完全图。
\((2)\) \(\chi(G) = 2\) 当且仅当 \(G\) 是有边二分图。
\((3)\) \(\chi(C_\nu) = \begin{cases}2,\quad \nu\,是偶数,\\3, \quad \nu\,是奇数。\end{cases}\)
\((4)\) 若图 \(H\) 是 \(G\) 的子图,则 \(\chi(H)\le \chi(G)\)。
定理 \(7.1\) 对任何图 \(G\),\(\chi(G) \le \Delta(G)+1\)。
证明
考虑给 \(v \in V\) 依次染上 \(1 \sim \Delta+1\) 中的颜色。
在给任意 \(v\) 着色时,其相邻的顶点至多只有 \(\deg(v) \le \Delta\) 个顶点着色,由抽屉原理还有至少一种颜色未被使用,直接着色即可。
定理 \(7.2(\text{Brooks})\) 设 \(\nu(\nu \ge 3)\) 阶连通图 \(G\) 不是完全图也不是奇圈,则 \(\chi(G) \le \Delta(G)\)。
边着色
定义 \(7.2\) 图 \(G\) 的一个 \(k\)-边着色是指把 \(k\) 种颜色 \(1,2,\cdots ,k\) 分配给图 \(G\) 的边,使每条边都分配一种颜色;若相邻边异色,则称这种边着色为一个正常 \(k\)-边着色。若图 \(G\) 有一个正常 \(k\)-边着色,则称 \(G\) 是可 \(k\)-边着色的。图 \(G\) 的边色数指的是使得图 \(G\) 可正常边着色的最少颜色数 \(k\),记为 \(\chi'(G)\)。
类似于顶点着色,图 \(G\) 的一个正常 \(k\)-边着色可以用代数的方式表示为边集合 \(E(G)\) 的一个划分 \(\mathcal{C}=(E_1,E_2,\cdots ,E_k)\),其中 \(E_i\) 表示着 \(i\) 色的边子集(可能是空集),满足:
\((1)\) \(E(G) = E_1 \cup E_2 \cup \cdots \cup E_k\);
\((2)\) \(E_i \cap E_j = \varnothing,1 \le i \ne j \le k\);
\((3)\) 任给 \(1 \le i \le k\),且任给 \(e_1,e_2 \in E_i\),\(e_1\) 与 \(e_2\) 都不相邻。
在进行正常 \(k\)-边着色时,若要求每种颜色都必须用到,则还需满足下面的第 \((4)\) 个条件;否则不需要。
\((4)\) 任给 \(1 \le i \le k,E_i \ne \varnothing\)。
显然 \(\Delta(G) \le \chi'(G) \le \varepsilon(G)\)。
引理 \(7.1\) 若连通图 \(G\) 不是奇圈,则存在一种 \(2\)-边着色,使得所用的两种颜色在每个度数大于等于 \(2\) 的顶点处都出现,即每个度数大于等于 \(2\) 的顶点所关联的边用到了这两种颜色。
证明
考虑将 \(G\) 中奇度点 \(S\) 两两匹配得到 \((s_1,t_1),(s_2,t_2),\cdots,(s_k,t_k)\),加入这些边 \((s_i,t_i)\) 得到一个 \(\text{Euler}\) 图 \(G^*\)。从一个 \(\deg(v)>2\) 的点 \(v\) 开始找 \(\text{Euler}\) 回路(第一条边优先找新加入的,若没有 \(\deg(v)>2\) 的点则优先找一个在 \(G\) 中是奇度数的)。
沿着 \(\text{Euler}\) 回路上边的顺序交替着色,若回路长为偶数则首尾颜色不同,\(G^*\) 中每个点关联的两种颜色的边数相等,满足条件。若回路长为奇数,删边后仅有起点 \(v\) 可能不满足,但若 \(\deg(v)>2\),故 \(v\) 有两条边在回路中以非首尾的方式相邻,满足条件。反之,唯一不成立的情况是任意 \(v\) 均有 \(\deg(v) \le 2\) 且回路长度为奇数,也就是奇圈。
给定图 \(G\) 的 \(k\)-边着色 \(\mathcal{C}\),用 \(c(v)\) 表示顶点 \(v\) 关联的边中出现的颜色数。显然 \(c(v) \le \deg(v)\)。\(\mathcal{C}\) 是正常 \(k\)-边着色,当且仅当等号对 \(G\) 中所有顶点 \(v\) 都成立。
定义 \(7.3\) 设 \(\mathcal{C}\) 和 \(\mathcal{C}'\) 是图 \(G\) 的两种 \(k\)-边着色,如果 \(\sum\limits_{v \in V(G)} c(v) < \sum\limits_{v \in V(G)} c'(v)\),则称 \(k\)-边着色 \(\mathcal{C}'\) 是对 \(\mathcal{C}\) 的一个改进,其中 \(c(v)\) 与 \(c'(v)\) 分别表示用 \(\mathcal{C}, \mathcal{C}'\) 着色时顶点 \(v\) 关联的边中出现的颜色数。不能再改进的 \(k\)-边着色称为最佳 \(k\)-边着色。
对于任意的着色 \(\mathcal{C}\) 来说,显然有 \(c(v) \le \deg(v)\),所以有 \(\sum\limits_{v \in V(G)} c(v) \le \sum\limits_{v \in V(G)} \deg(v)\)。而 \(\mathcal{C}\) 是正常 \(k\)-边着色,当且仅当对 \(G\) 中所有顶点 \(v\),都有 \(c(v) = \deg(v)\),此时满足 \(\sum\limits_{v \in V(G)} c(v) = \sum\limits_{v \in V(G)} \deg(v)\)。所以对于正常边着色 \(\mathcal{C}\) 来说,\(\sum\limits_{v \in V(G)} c(v)\) 达到最大值。利用定义 \(7.3\),可以表示一个边着色方案偏离正常边着色方案的程度。
引理 \(7.2\) 设 \(\mathcal{C} =(E_1,E_2,\cdots ,E_k)\) 是图 \(G\) 的一个最佳 \(k\)-边着色。如果存在一个顶点 \(v_0\) 和两种颜色 \(i\) 与 \(j\),使得 \(i\) 色不在 \(v_0\) 关联的边中出现,但 \(j\) 色在 \(v_0\) 关联的边中至少出现两次,则边导出子图 \(G[E_i \cup E_j]\) 中含 \(v_0\) 的连通片是一个奇圈。
证明
考虑 \(G[E_i \cup E_j]\) 中含 \(v_0\) 的连通片 \(H\)。反证,若 \(H\) 不是奇圈,则由引理 \(7.1\),存在一种边着色方案使得它的 \(2\) 种颜色在 \(H\) 中度数至少为 \(2\) 的顶点所关联的边中都出现。此时替换为这种边着色方案,\(v_0\) 关联的边会多一种颜色 \(i\),\(c'(v_0)=c(v_0)+1\),那么就得到了 \(\mathcal{C}\) 的一个改进,与最佳着色矛盾。故 \(G[E_i \cup E_j]\) 中含 \(v_0\) 的连通片是奇圈。
定理 \(7.3\) 若 \(G\) 是二分图,则 \(\chi'(G)=\Delta(G)\)。
证明
显然 \(\chi'(G) \ge \Delta(G)\),只需证 \(G\) 可 \(\Delta\)-着色即可。反正,假设不能,则考虑 \(G\) 的最佳 \(\Delta\)-边着色。存在 \(v\) 满足 \(c(v)<\deg(v)\le \Delta\)。那么由抽屉原理,存在颜色 \(i\) 在 \(v\) 关联的边中没有出现,存在颜色 \(j\) 在 \(v\) 关联的边中至少出现两次。那么由引理 \(7.2\),\(G\) 中存在奇圈,与二分图矛盾。故 \(\chi'(G)=\Delta(G)\)。
定理 \(7.4(\text{Vizing})\) 若 \(G\) 是简单图,则 \(\chi'(G)= \Delta(G)\) 或 \(\Delta(G)+1\)。
证明
只需反证 \(\chi'(G)>\Delta(G)+1\) 不成立即可。找到最佳 \((\Delta+1)\)-边着色,通过两次构造奇圈来证明不为奇圈。具体证明细节较多,这里不展开证明,感兴趣的读者可以自行了解。
实际上,\(\text{Vizing}\) 证明了比上述定理更一般的结论,它对所有无环图都正确。定义 \(G\) 中连接两个顶点的最大边数称为 \(G\) 的重数,记为 \(\mu(G)\)。\(\text{Vizing}\) 定理的一般形式为:若 \(G\) 是无环图,则 \(\Delta \le \chi' \le \Delta+\mu\)。
我们称满足 \(\chi'(G) = \Delta(G)\) 的图为第一类图,否则为第二类图。二分图属于第一类,\(\text{Petersen}\) 图属于第二类。尽管定理 \(7.4\) 很强,仍然留下一个尚未解决的问题:如何判定任意一个图是否为第一类图,至今尚无有效算法,这个问题的重要性在平面图的边着色时更为明显。
边着色的一个典型应用就是“课表安排问题”。假设某学校有 \(m\) 位教师 \(x_1, x_2,\cdots ,x_m\) 和 \(n\) 个班级 \(y_1,y_2,\cdots ,y_n\)。已知某一天教师 \(x_i\) 需要给班级 \(y_j\) 上 \(p_{i,j}\) 节课,要求设计一张课时尽量少的课表,至少需要多少个教室?或者在不增加课时的情况下,能否给出一个最节省教室的课表?
首先建立图模型,每个顶点表示教师或者班级,即有两类顶点:\(X={x_1,x_2,\cdots ,x_m}\) 表示教师集合,\(Y ={y_1,y_2,\cdots ,y_n}\) 表示班级集合。顶点 \(x_i\) 和顶点 \(y_j\) 之间连接 \(p_{i,j}\) 条边,当且仅当教师 \(x_i\) 需要给班级 \(y_j\) 上 \(p_{i,j}\) 节课。如此,得到二分图 \(G=(X,E,Y)\)。因为在任何一节课时内,每位教师最多教一个班级,并且每个班级最多只能由一位教师讲课。故我们需要找到 \(G\) 的一个正常边着色,由于 \(G\) 为二分图,故 \(\chi'(G)=\Delta(G)\),安排一张 \(\Delta\) 课时的课表即可,且可以在多项式时间内给出一个着色方案。
假设所有老师给所有班级共计上 \(l\) 节课,而需要编制一张 \(p\) 课时的课表。由上面的讨论知,\(p \ge \Delta\),平均每一课时至少需同时开 \(l/p\) 节课,因此在某一课时里至少需要 \(\lceil l/p \rceil\) 个教室。下面的引理和定理从理论上保证了在一张 \(p\) 课时的课表里总可以安排完 \(l\) 节课,使得在一节课时里最多占用 \(\lceil l/p \rceil\) 个教室。
引理 \(7.3\) 设 \(M\) 和 \(N\) 是图 \(G\) 中两个无公共边匹配,且 \(|M|>|N|\),则存在 \(G\) 中两个无公共边的匹配 \(M'\) 和 \(N'\),使得 \(|M'| = |M|-1\),\(|N'| = |N|+1\),\(M'\cup N' = M \cup N\)。
证明
考虑 \(H=G[M \cup N]\),由于 \(|M|>|N|\),故 \(H\) 中某个连通片是长度为奇数的轨道 \(P=v_0e_1v_1\cdots e_{2k+1}v_{2k+1}\),其中第一条和最后一条边都在 \(M\) 中,\(M\) 中和 \(N\) 中的边交错出现。
令 \(M'=(M - \{e_1,e_3,\cdots ,e_{2k+1} \})\cup \{e_2,e_4,\cdots ,e_{2k}\}\),\(N' =(N - \{e_2,e_4,\cdots ,e_{2k}\})\cup\{e_1,e_3,\cdots ,e_{2k+1}\}\)。显然 \(M',N'\) 符合条件,证毕。
定理 \(7.5\) 设 \(G\) 是二分图,\(\Delta \le p\),则存在 \(G\) 的 \(p\) 个不相交匹配 \(M_1,M_2,\cdots ,M_p\),使得 \(E(G) = \bigcup\limits_{i=1}^p M_i\),且对 \(1 \le i \le p\),\(\lfloor \varepsilon / p \rfloor \le |M_i| \le \lceil \varepsilon / p \rceil\)。
证明
二分图的边色数是 \(\Delta\),所以 \(G\) 的边集可以划分成 \(\Delta\) 个匹配 \(M'_1,M'_2,\cdots ,M'_\Delta\)。故对于任意 \(p \ge \Delta\),令 \(M'_ i = \varnothing (\Delta < i \le p)\),则得到 \(G\) 的 \(p\) 个无公共边的匹配 \(M'_1,M'_2,\cdots ,M'_p\),使得 \(E(G) = \bigcup^p_{i=1} M'_i\)。对于边数相差超过 \(1\) 的任何两个匹配,反复应用引理 \(7.3\),最后就能得到 \(G\) 的 \(p\) 个无公共边的匹配,满足定理的结论。证毕。
该定理说明任意两个匹配的边数最多相差 \(1\)。
平面图着色
后记
学习图论,我们更应该注重自然语言的描述,以清楚、明白地解决问题,同时也要注重思维的训练,学习更多解决问题的方法。
反证法:正难则反,主要利用逆否命题。
归纳法:缩小问题规模,主要利用原问题和子问题相同的问题结构。
推理法:先猜后证,主要利用断言进行问题的简化。
少废话,你 GPA 多少?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号