南昌航空大学 软件学院 pta java 第二阶段总结
国庆回来没多久就第二次阶段总结了。
只能感慨,时间如流水般流逝。我还没写完呢

虽然但是,题目还是认真写的,每个字符都饱含我的深情。
三次作业和博客的代码我贴在别的博客里了,链接我贴在下面了。我会挑选一些题目进行具体分析。
目录
完整作业代码
前言
题量
三次作业题量分别是323,期中考试有3题,不算很高的题量。
难度和知识点
第四次第五次的难度远高于其他一次和期中考试,特别是第五次。但总体来说,考察的知识点是逐步增多的,第六次新添了继承和多态还有容器的内容
设计与分析
7-1 sdut-String-2 识蛟龙号载人深潜,立科技报国志(II)(正则表达式)
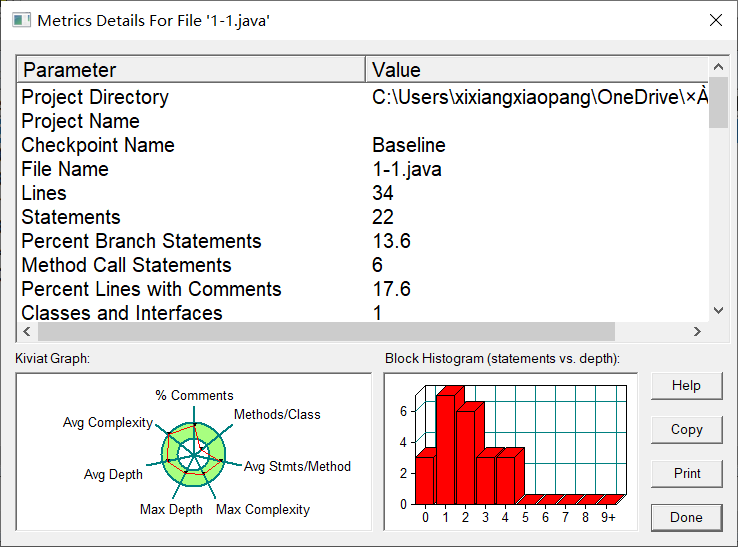
圈复杂度很正常
题目的意思就是将每行的数字提取出来,然后相加,对每行的处理作为一个方法,
while (!a.ch.equals("end")){
int ans =a.Solve2();//读入答案
System.out.printf(ans+"\n");
a.ch = input.nextLine();//读入
}
再对数字进行一个提取就行,正则表达式用在了判断字符串中是否有数字,当然也可以直接进行简单的字符串遍历。
int num=0,temp=0;
for(int i=0;i<ch.length();i++) {
while(i<ch.length()&&ch.charAt(i)>='0'&&ch.charAt(i)<='9'){
temp*=10;
temp+=(int)(ch.charAt(i)-'0');
// System.out.printf(temp+" ");
i++;
}
num+=temp;
temp=0;
}
return num;
题目很简单,没啥复杂度或者其他的说法。
7-2 点线形系列4-凸四边形的计算
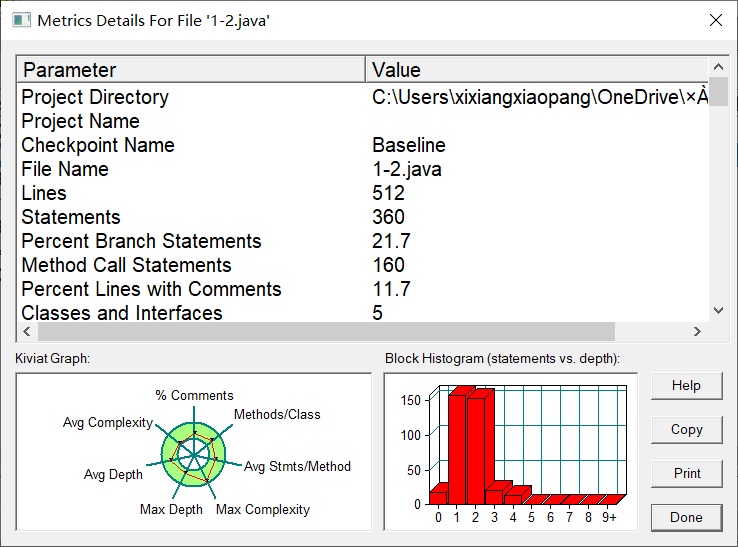
主要是solve方法的圈复杂度太高了。。。
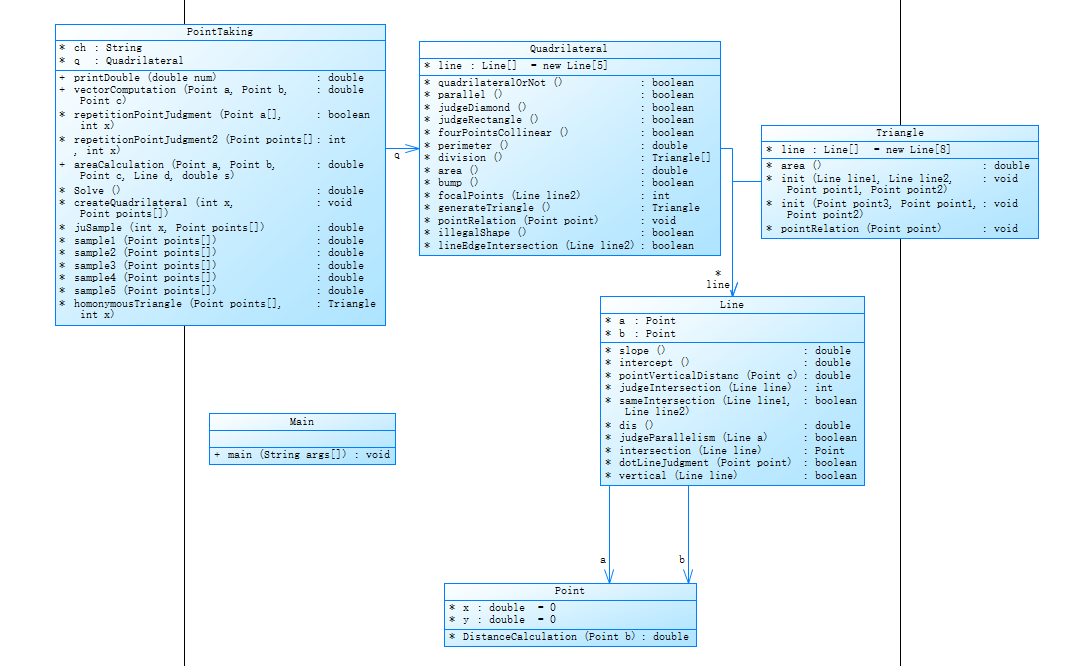
case1
判断是否为四边形,主要是判断是否有三个点共线或者是生成俩三角形。
if(q.quadrilateralOrNot()){
System.out.print("false false");
return 5;
}
if(q.parallel())
System.out.print("true true");
else System.out.print("true false");
case2
判断四条直线是否等长以及判断相交直线是否都垂直来判断是否为菱形和矩形,二者均符合则为正方形
if(q.quadrilateralOrNot() || repetitionPointJudgment(points,4))
return -4;
boolean flag1,flag2;
flag1=q.judgeDiamond();
flag2=q.judgeRectangle();
if(flag1&&flag2)
System.out.print("true true true");
else if(flag1)
System.out.print("true false false");
else if(flag2)
System.out.print("false true false");
else
System.out.print("false false false");
case3
多次分割四边形并计算面积,如果多次面积一样,就是凸四边形,反之则为凹四边形。
double sample3(Point[] points){
if(repetitionPointJudgment(points,4))
return -4;
if(q.bump())
System.out.printf("true ");
else System.out.printf("false ");
System.out.printf(printDouble(q.perimeter())+" "+printDouble(q.area()));
case4
最难的一个case,但我没时间了,就没写hhhh,后面第五次作业的时候把这个写完了,但已经为时已晚。
if(q.fourPointsCollinear()||q.illegalShape())
return -5;
Line line= new Line();
line.a=points[1];line.b=points[2];
if(q.lineEdgeIntersection(line)) {
System.out.printf("The line is coincide with one of the lines");
return 5;
}
int num = q.focalPoints(line);
System.out.printf(num+"");
if(num<2){
return 5;
}
Quadrilateral[] qua = new Quadrilateral[3];
return 5;
case5
点线法秒了

其实就是以点和四边形的点进行连接生成三角形,然后计算面积查看是否相等,特判一下是否在边上。
Triangle tri;
int num = repetitionPointJudgment2(points, 5);
if (num > 1||q.fourPointsCollinear()||q.illegalShape())
return -5;
if (num == 1) {
tri = homonymousTriangle(points,2);
tri.pointRelation(points[1]);
return 5;
}
if (q.line[1].slope() == q.line[2].slope() || q.line[2].slope() == q.line[3].slope() || q.line[3].slope() == q.line[4].slope() || q.line[4].slope() == q.line[1].slope()) {
tri = q.generateTriangle();
tri.pointRelation(points[1]);
return 5;
}
q.pointRelation(points[1]);
return 5;
Quadrilateral类
class Quadrilateral {
Line []line = new Line[5];
boolean quadrilateralOrNot(){
return line[1].judgeIntersection(line[3])==1|| line[2].judgeIntersection(line[4]) ==1 || line[1].dotLineJudgment(line[3].a) || line[1].dotLineJudgment(line[3].b) || line[3].dotLineJudgment(line[1].a) || line[3].dotLineJudgment(line[1].b);
}
boolean parallel(){//判断平行四边形
return line[1].slope() == line[3].slope() && line[2].slope() == line[4].slope();
}
boolean judgeDiamond(){//判断是否菱形
return parallel()&&Math.abs(line[1].dis()-line[2].dis())<0.05;
}
boolean judgeRectangle(){//判断矩形
return line[1].vertical(line[2])&&line[1].judgeParallelism(line[3])&&line[2].judgeParallelism(line[4]);
}
boolean fourPointsCollinear(){//判断不能组成三角形或者四边形
// System.out.printf(line[1].slope()+" "+line[2].slope()+" "+line[3].slope()+" "+line[4].slope()+"\n");
return line[1].slope()==line[2].slope()&&line[2].slope()==line[3].slope()&&line[3].slope()==line[4].slope();
}
double perimeter(){//周长
return line[1].dis()+line[2].dis()+line[3].dis()+line[4].dis();
}
Triangle[] division(){//划分三角形
Line a = new Line(),b = new Line();
Triangle [] tri = new Triangle[5];
for(int i=1;i<=4;i++)
tri[i]= new Triangle();
a.a=line[1].a;a.b=line[3].a;
b.a=line[1].b;b.b=line[3].b;
tri[1].line[1]=line[1];
tri[1].line[2]=line[2];
tri[1].line[3]=a;
tri[2].line[1]=line[3];
tri[2].line[2]=line[4];
tri[2].line[3]=a;
tri[3].line[1]=line[1];
tri[3].line[2]=line[4];
tri[3].line[3]=b;
tri[4].line[1]=line[3];
tri[4].line[2]=line[2];
tri[4].line[3]=b;
return tri;
}
double area(){//面积
Triangle [] tri = division();
return Math.min(tri[1].area()+tri[2].area(),tri[3].area()+tri[4].area());
}
boolean bump(){//判断凹凸
Triangle [] tri = division();
return tri[1].area() + tri[2].area() == tri[3].area() + tri[4].area();
}
int focalPoints(Line line2) {//求线与其焦点数量
int num=0;
boolean []flag={false,false,false,false,false};
for(int i=1;i<=4;i++) {
if (line2.judgeIntersection(line[i]) == 1) {
num++;
flag[i] = true;
}
//System.out.printf(num + "\n");
}
// for(int i=1;i<=4;i++){
// if(flag[i]&&line2.sameIntersection(line[i],line[i%4+1]))
// num--;
// // System.out.printf(num+"\n");
// }
return num;
}//4:-1,-1 1,1 0,0 2,0 3,0 0,5
//4:-1,-1 1,1 0,0 5,0 5,5 0,5
Triangle generateTriangle(){
Triangle tri = new Triangle();
if(line[1].slope()==line[2].slope())
tri.init(line[3],line[4],line[1].a,line[2].b);
else if(line[3].slope()==line[2].slope())
tri.init(line[4],line[1],line[2].a,line[3].b);
else if(line[3].slope()==line[4].slope())
tri.init(line[1],line[2],line[3].a,line[4].b);
else if(line[1].slope()==line[4].slope())
tri.init(line[2],line[3],line[4].a,line[1].b);
return tri;
}
void pointRelation(Point point){
Triangle a=new Triangle(),b= new Triangle(),c= new Triangle(),d= new Triangle();
b.init(point,line[3].a,line[3].b);c.init(point,line[2].a,line[2].b);d.init(point,line[1].a,line[1].b);
a.init(point,line[4].a,line[4].b);
if((d.area()==0||b.area()==0||c.area()==0||a.area()==0)&&(Math.abs(area()-a.area()-b.area()-c.area()-d.area())<0.0005))
System.out.println("on the quadrilateral");
else if(Math.abs(area()-a.area()-b.area()-c.area()-d.area())<0.0005)
System.out.printf("in the quadrilateral");
else
System.out.println("outof the quadrilateral");
}
boolean illegalShape(){
for (int i=1;i<=4;i++)
if(line[i].slope()==line[i%4+1].slope()){
if((line[i].a.x>line[i].b.x&&line[i%4+1].b.x>line[i%4+1].a.x)||
(line[i].a.x<line[i].b.x&&line[i%4+1].b.x<line[i%4+1].a.x)||
(line[i].a.y>line[i].b.y&&line[i%4+1].b.y>line[i%4+1].a.y)||
(line[i].a.y<line[i].b.y&&line[i%4+1].b.y<line[i%4+1].a.y))
return true;
}
return false;
}
// Quadrilateral[] division(Quadrilateral q,Line line2){
// return q;
// }
boolean lineEdgeIntersection(Line line2){
return line2.judgeIntersection(line[1]) == 0 || line2.judgeIntersection(line[2]) == 0 ||
line2.judgeIntersection(line[3]) == 0 || line2.judgeIntersection(line[4]) == 0;
}
}
7-3 设计一个银行业务类
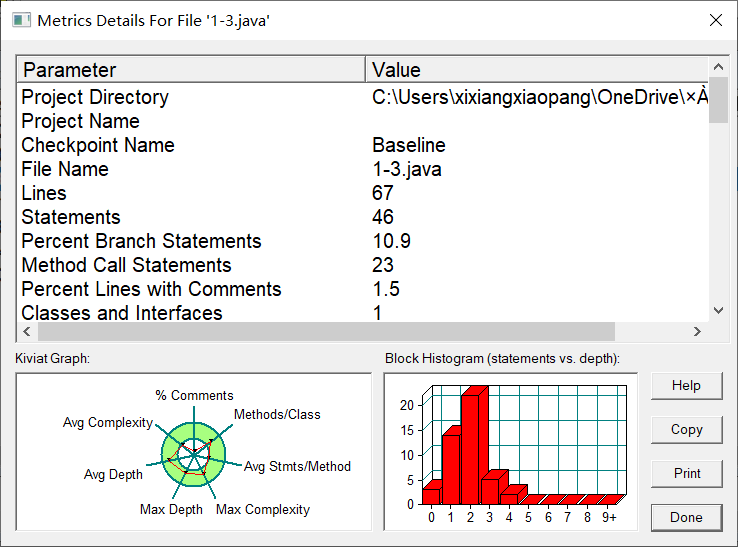
圈复杂度微微超标

经典按图说话,话说这两题出现的意义就是衬托第二题吧==。
题目只需要一个BankBusiness类,除去这个类加一个简单调用的Main类就行,最好把错误类型也封装成方法。
贴一下BankBusiness类。
class BankBusiness {
Scanner input = new Scanner(System.in);
public static String bankName= "中国银行";
public static double balance=0;
private static String name,password;
public static void welcome(){
System.out.printf(bankName+"欢迎您的到来!\n");
}
void init(){
name = input.next();
password = input.next();
welcome();
deposit();
withdraw();
withdraw();
withdraw();
welcomeNext();
}
public boolean verification() {
String inputName = input.next();
if(inputName.equals(password))
return true;
return false;
}
public void error1(){
System.out.printf("您的密码错误!\n");
}
public void deposit(){
boolean flag = verification();
Double inputNum = input.nextDouble();
if(!flag) error1();
else{
balance += inputNum;
System.out.printf("您的余额有%.1f元。\n",(float)(balance));
}
}
public void withdraw(){
boolean flag = verification();
Double inputNum = input.nextDouble();
if(!flag) error1();
else{
if(balance>=inputNum){
balance -= inputNum;
System.out.printf("请取走钞票,您的余额还有%.1f元。\n",(float)(balance));
}
else
System.out.printf("您的余额不足!\n");
}
}
public static void welcomeNext(){
System.out.printf("请收好您的证件和物品,欢迎您下次光临!");
}
}
7-1 点线形系列5-凸五边形的计算-1
这是第二难的题目了(第一难的我没写),之前的类写的太烂了,后面的过程中,全程在修改类,太痛苦了啊。

痛定思痛,整顿好所有类准备大展身手,发现快截止了。
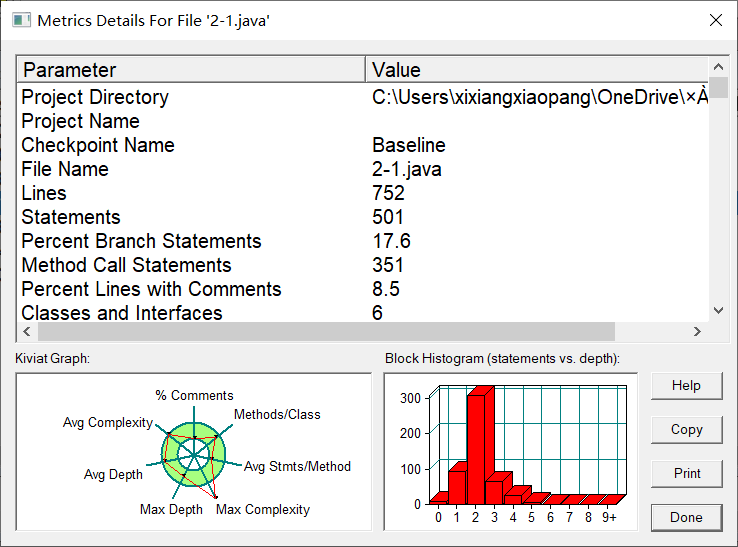
我都没时间去整理PointTake类的几个高复杂度的方法,所以复杂度有点抽象。
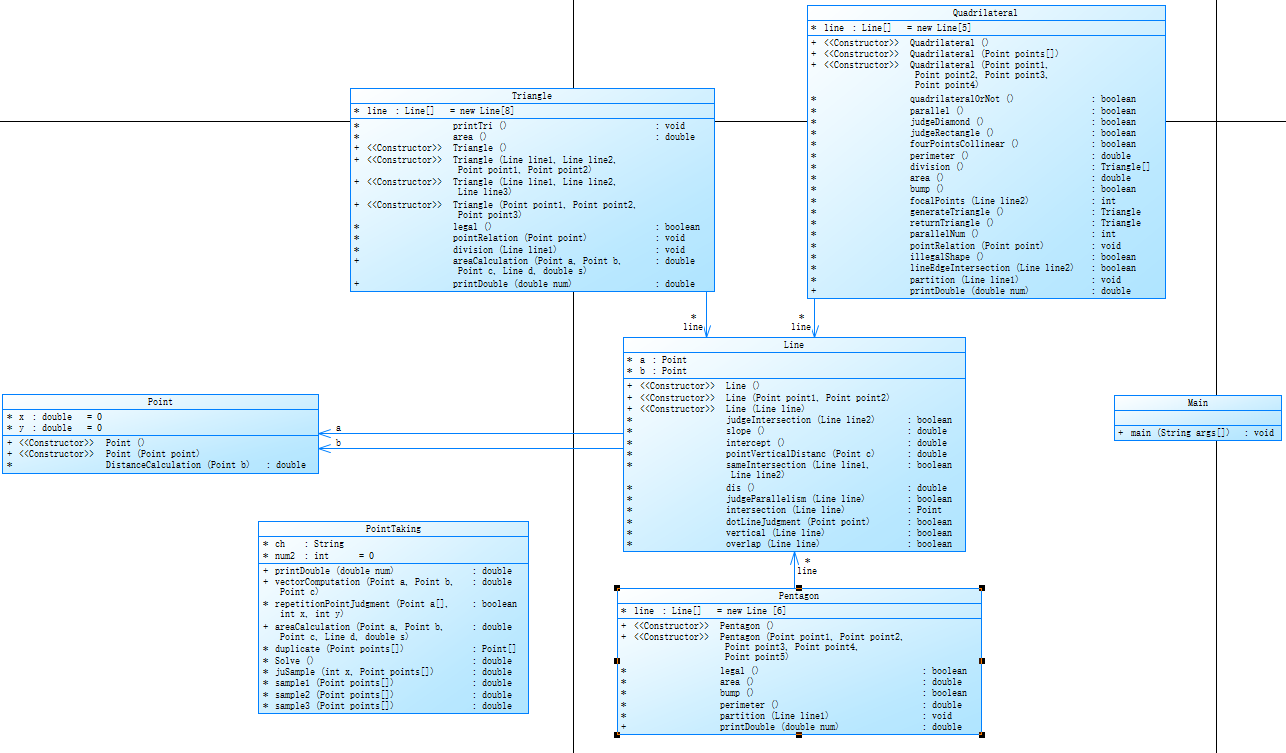
case1
判断相邻两线不平行以及相隔一条线的两条线不相交。
Pentagon pentagon = new Pentagon(points[1],points[2],points[3],points[4],points[5]);
if(!pentagon.legal()||repetitionPointJudgment(points,1,5))
return 2;
return 1;
case2
和四边形的方法一样,多次分割计算面积,一样则凸,反之则凹。
if(sample1(points)==2)
return -4;
Pentagon pentagon = new Pentagon(points[1],points[2],points[3],points[4],points[5]);
if(pentagon.bump())
return 2;
// System.out.printf(q.bump()+"\n");
System.out.printf("true "+printDouble(pentagon.perimeter())+" "+printDouble(pentagon.area()));
return 5;
case3
判断图形,然后分割并计算面积。
if(points[1].x==points[2].x&&points[1].y == points[2].y)
return 4;
Line line = new Line(points[1],points[2]);
Triangle tri = new Triangle();
Quadrilateral qua = new Quadrilateral();
Point []point = duplicate(points);
if(num2==3) {
tri = new Triangle(point[1],point[2],point[3]);
tri.division(line);
}
else if(num2==4){
qua = new Quadrilateral(point);
qua.partition(line);
}
else{
Pentagon pent = new Pentagon(points[3],points[4],points[5],points[6],points[7]);
pent.partition(line);
}
return 5;
Pentagon
class Pentagon {
Line[] line = new Line [6];
public Pentagon(){}
public Pentagon(Point point1,Point point2,Point point3,Point point4,Point point5) {
for(int i=1;i<=5;i++){
line[i] = new Line();
line[i].a = new Point();
line[i].b = new Point();
}
line[1].a.x = point1.x;line[1].a.y = point1.y;
line[1].b.x = point2.x;line[1].b.y = point2.y;
line[2].a.x = point2.x;line[2].a.y = point2.y;
line[2].b.x = point3.x;line[2].b.y = point3.y;
line[3].a.x = point3.x;line[3].a.y = point3.y;
line[3].b.x = point4.x;line[3].b.y = point4.y;
line[4].a.x = point4.x;line[4].a.y = point4.y;
line[4].b.x = point5.x;line[4].b.y = point5.y;
line[5].a.x = point5.x;line[5].a.y = point5.y;
line[5].b.x = point1.x;line[5].b.y = point1.y;
}
boolean legal(){
for(int i=1;i<=5;i++) {
// System.out.printf("%f %f\n",line[i].a.x,line[i].a.y);
if ((line[i].a.x-line[i].b.x )*(line[i%5+1].a.y-line[i%5+1].b.y)== (line[i%5+1].a.x-line[i%5+1].b.x )*(line[i].a.y-line[i].b.y))
return false;
}
for(int i=1;i<=5;i++){
for (int j=1;j<=5;j++){
if(j!=(i%5+1)&&j!=(i+3)%5+1&&i!=j) {
// System.out.printf("%f %f %f %f\n",line[i].a.x,line[i].a.y,line[j].a.x,line[j].a.y);
if (line[i].judgeIntersection(line[j]))
return false;
}
}
}
return true;
}
double area(){
Triangle []tri=new Triangle[5];
Line[] lines= new Line[4];
lines[1] = new Line(line[1].a,line[2].b);
lines[2] = new Line(line[1].a,line[3].b);
tri[1]= new Triangle(line[1],line[2],lines[1]);
tri[2]= new Triangle(lines[1],line[3],lines[2]);
tri[3]= new Triangle(lines[2],line[4],line[5]);
return tri[1].area()+tri[2].area()+tri[3].area();
}
boolean bump(){//判断凹凸,凹为true
Triangle []tri=new Triangle[5];
Line[] lines= new Line[4];
double num = 0,temp = 0;
lines[1] = new Line(line[1].a,line[2].b);
lines[2] = new Line(line[1].a,line[3].b);
tri[1]= new Triangle(line[1],line[2],lines[1]);
tri[2]= new Triangle(lines[1],line[3],lines[2]);
tri[3]= new Triangle(lines[2],line[4],line[5]);
num = tri[1].area()+tri[2].area()+tri[3].area();
for(int i = 2;i<=5;i++){
lines[1]=new Line(line[i].a,line[i%5+1].b);
lines[2]=new Line(line[i].a,line[(i+1)%5+1].b);
tri[1]= new Triangle(line[i],line[i%5+1],lines[1]);
tri[2]= new Triangle(lines[1],line[(i+1)%5+1],lines[2]);
tri[3]=new Triangle(lines[2],line[(i+2)%5+1],line[(i+3)%5+1]);
temp = tri[1].area()+tri[2].area()+tri[3].area();
if(Math.abs(temp-num)>0.005)
return true;
}
return false;
}
double perimeter(){
return line[1].dis()+line[2].dis()+line[3].dis()+line[4].dis()+line[5].dis();
}
void partition(Line line1){
Quadrilateral qua = new Quadrilateral();
System.out.printf("2 ");
double s = area(),s2=0;
boolean f= false;
Triangle tri = new Triangle();
A:for(int i= 1;i <=5;i++){
if((line1.judgeIntersection(line[i])&&line1.judgeIntersection(line[i%5+1])&&!line1.judgeIntersection(line[(i+1)%5+1])&&
line1.judgeIntersection(line[(i+2)%5+1])&&line1.judgeIntersection(line[(i+3)%5+1])&&
(line1.sameIntersection(line[i],line[i%5+1])&&line1.sameIntersection(line[(i+3)%5+1],line[(i+2)%5+1])))||
(line1.judgeIntersection(line[i])&&line1.judgeIntersection(line[i%5+1])&&!line1.judgeIntersection(line[(i+1)%5+1])
&&!line1.judgeIntersection(line[(i+2)%5+1]) &&line1.judgeIntersection(line[(i+3)%5+1])
&&(line1.sameIntersection(line[i],line[i%5+1])))||
(line1.judgeIntersection(line[i])&&!line1.judgeIntersection(line[i%5+1])&&!line1.judgeIntersection(line[(i+1)%5+1])
&&line1.judgeIntersection(line[(i+2)%5+1]) &&line1.judgeIntersection(line[(i+3)%5+1])
&&(line1.sameIntersection(line[(i+3)%5+1],line[(i+2)%5+1])))||
(line1.judgeIntersection(line[i])&&!line1.judgeIntersection(line[i%5+1])&&!line1.judgeIntersection(line[(i+1)%5+1])&&!line1.judgeIntersection(line[(i+2)%5+1])&&line1.judgeIntersection(line[(i+3)%5+1]))){
tri = new Triangle(line[i].a,line1.intersection(line[i]),line1.intersection(line[(i+3)%5+1]));
s2 = tri.area();
f = true;
break A;
}
}
B:for(int i=1;i<=5;i++){
if((!line1.judgeIntersection(line[i])&&line1.judgeIntersection(line[i%5+1])&&!line1.judgeIntersection(line[(i+1)%5+1])&&//1
!line1.judgeIntersection(line[(i+2)%5+1])&&line1.judgeIntersection(line[(i+3)%5+1]))||
(!line1.judgeIntersection(line[i])&&line1.judgeIntersection(line[i%5+1])&&line1.judgeIntersection(line[(i+1)%5+1])&&//5
!line1.judgeIntersection(line[(i+2)%5+1])&&line1.judgeIntersection(line[(i+3)%5+1])&&
line1.sameIntersection(line[(i+1)%5+1],line[i%5+1]))){
qua = new Quadrilateral(line[i].a,line[i].b,line1.intersection(line[i%5+1]),line1.intersection(line[(i+3)%5+1]));
s2 = qua.area();
break B;
}
}
System.out.printf(printDouble(Math.min(s2,s-s2))+" "+printDouble(Math.max(s2,s-s2)));
}
public static double printDouble(double num) {
String str = String.format("%.3f",num);
num = Double.parseDouble(str);
return num;
}
}
7-2 点线形系列5-凸五边形的计算-2
我写到这里没时间了,写不完hhh,所以只能把这里空着了,巨麻。

7-1 点与线(类设计)
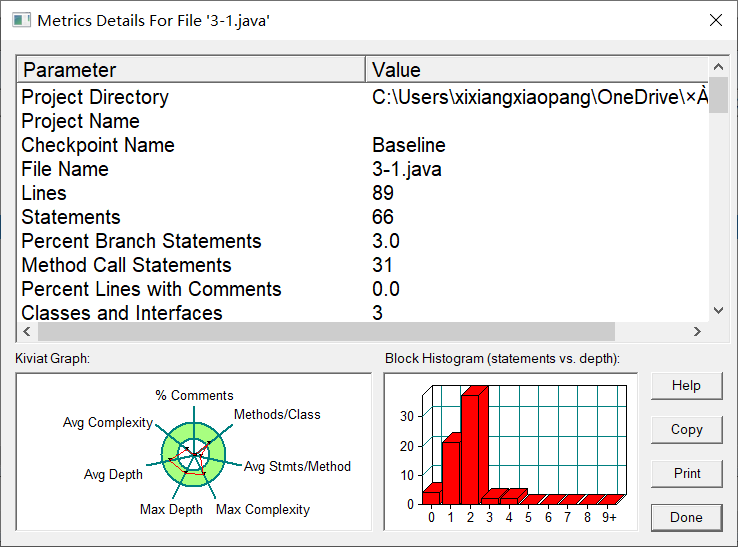

按照题目给的直接进行封装就行,一个Point类一个Line类,除了get、set方法外,就是距离和display,我把我的两个类放上来
Point
class Point {
private double x,y;
public Point(){
}
public Point(double x, double y){
setX(x);setY(y);
}
void setX(double x){
this.x =x;
}
void setY(double y){
this.y = y;
}
double getX(){
return this.x;
}
double getY(){
return this.y;
}
void display(){
double numx,numy;
String str1 = String.format("%.3f",getX()),str2 = String.format("%.3f",getY());
numx = Double.parseDouble(str1);numy = Double.parseDouble(str2);
System.out.printf("(%.2f,%.2f)",numx,numy);
}
}
Line
class Line {
Point point1,point2;
String color;
public Line(){}
public Line(Point point1, Point point2,String color){
setColor(color);setPoint1(point1) ;setPoint2(point2);
}
Point getPoint1(){return point1;}
Point getPoint2(){return point2;}
String getColor(){return color;}
void setPoint1(Point point1){
this.point1 = new Point(point1.getX(),point1.getY());
}
void setPoint2(Point point2){
this.point2 = new Point(point2.getX(),point2.getY());
}
void setColor(String color){
this.color = color;
}
double getDistance(){
return Math.sqrt((point1.getX()- point2.getX())*(point1.getX()- point2.getX())+(point1.getY()- point2.getY())*(point1.getY()- point2.getY()));
}
void display(){
System.out.printf("The line's color is:" +getColor()+
"\nThe line's begin point's Coordinate is:\n" );
point1.display();
System.out.printf("\n"+"The line's end point's Coordinate is:\n" );
point2.display() ;
System.out.printf("\n"+"The line's length is:" );
double num;
String str1 = String.format("%.3f",getDistance());
num= Double.parseDouble(str1);
System.out.printf("%.2f",num);
}
}
7-2 点线面问题重构(继承与多态)
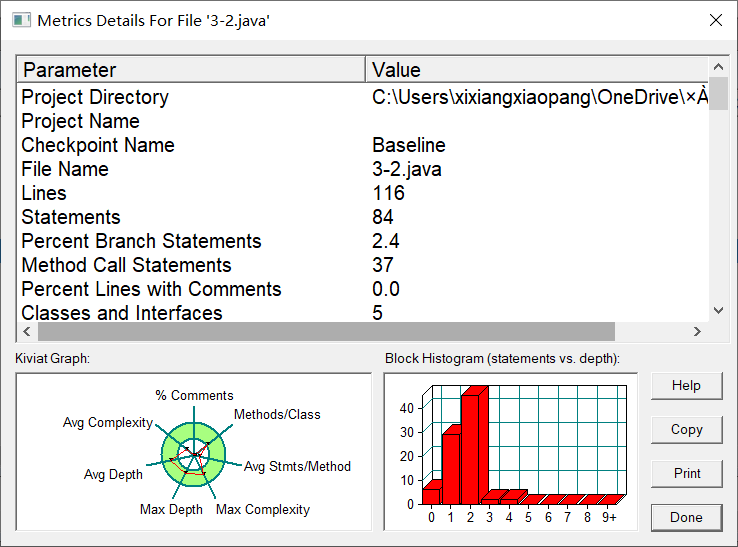
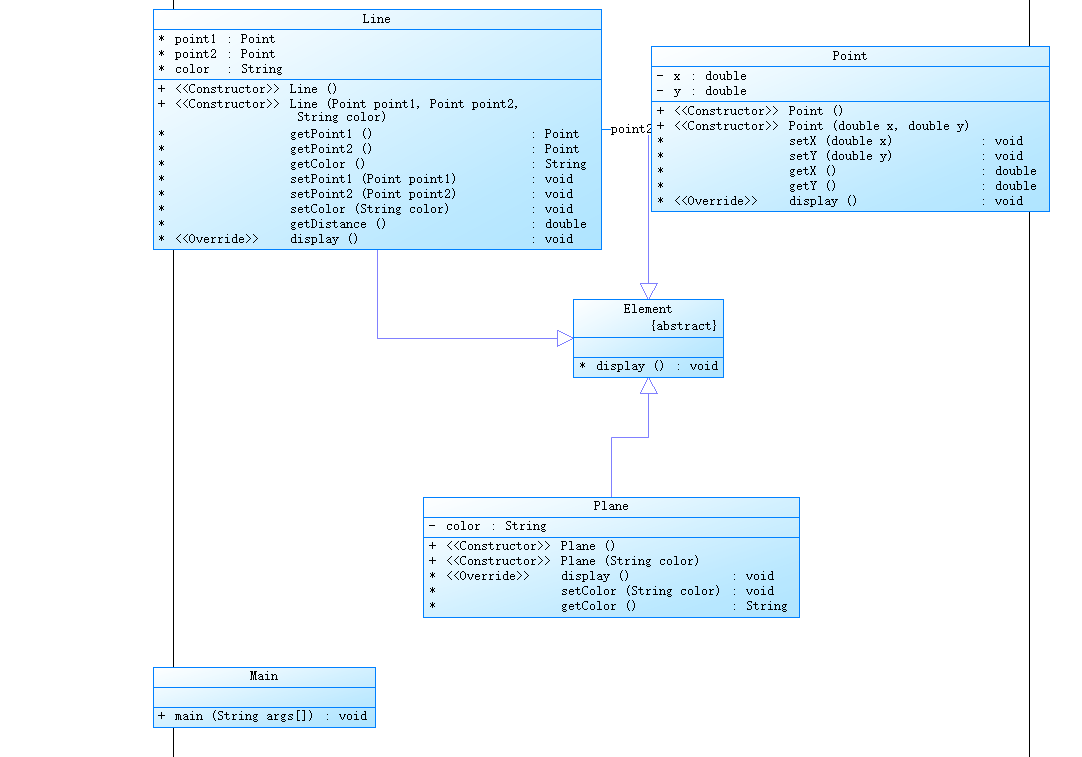
承接第一题,加了一个抽象类Element和平面类,平面类减少了难度,只剩下了颜色,我以为第三题会加大难度会让平面类边复杂,实际上第三题考别的东西去了
Element
abstract class Element{
abstract void display();
}
Plane
class Plane extends Element{
private String color;
public Plane(){}
public Plane(String color){
setColor(color);
}
void display(){
System.out.printf("The Plane's color is:"+getColor()+"\n");
};
void setColor(String color){this.color = color;}
String getColor(){return color;}
}
7-3 点线面问题再重构(容器类)
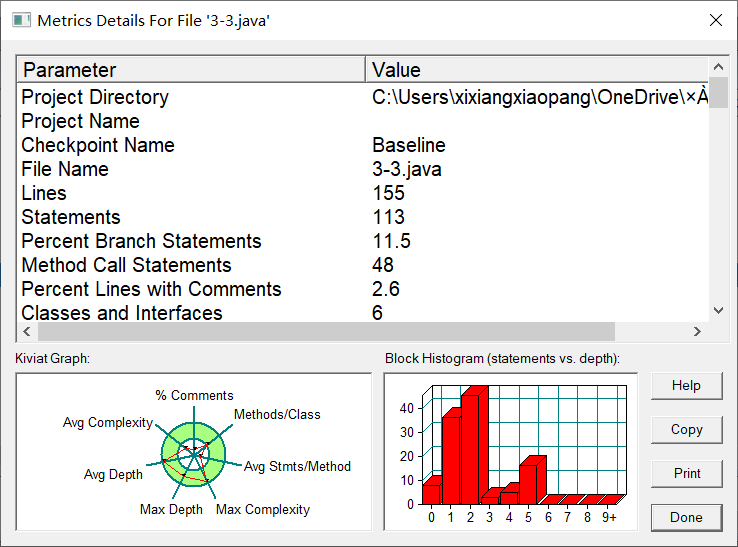
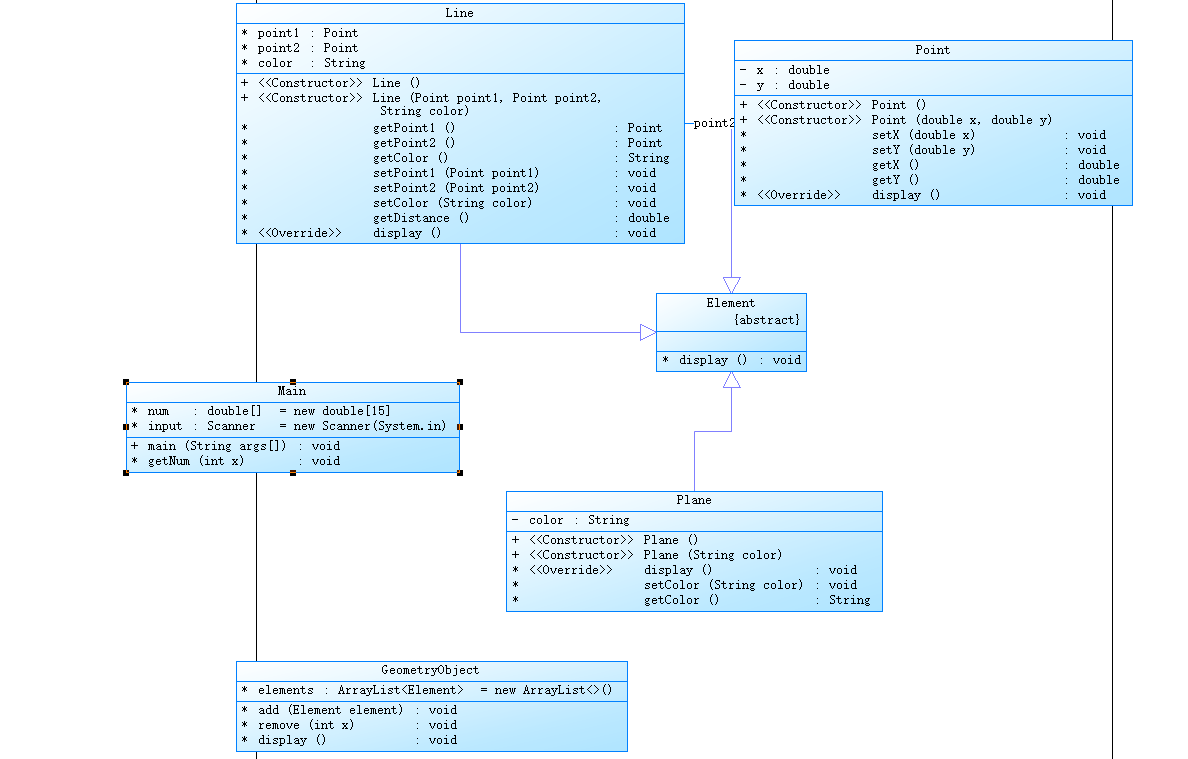
增加了一个容器类GeometryObject,用来盛放Element类,用起来确实方便很多很多,因为之前第六次作业做了有关容器的题目,所以当场debug少花了很多时间。
GeometryObject
class GeometryObject{
ArrayList<Element> elements = new ArrayList<>();
void add(Element element){
elements.add(element);
}
void remove(int x){
if(x>elements.size())
return;
elements.remove(x-1);
}
void display(){
for (Element ele:elements){
ele.display();
}
}
}
采坑心得
精度!
精度!!
精度!!!
因为精度的问题我点线图形类的题一直都有问题,包括但不仅于点在线上判断,两线与一线交点判断等等等等,每个错误都是血与泪,到后面我花了巨多巨多时间去整理,如果类的精度搞得好,其实可以快速过的。
然后就是方法,我一直用着三角形的方法,但是后面的多面体其实这些方法不适用了。
改进建议
题目承接很好,就是第五第六次难度骤降,可以稍微降低第五次难度然后提高第六次难度。
总结
时间管理错误,导致我有整整一题没写完,很糟糕的体验,但更糟糕的是疯狂改类改的我头昏脑涨。对于我个人知识点的掌握来说,是提升十分大的,使我掌握了多态和继承,也加深了对于封装的认知,提高了独立代码能力,以及个人综合能力。
那咱,下次见



 浙公网安备 33010602011771号
浙公网安备 33010602011771号